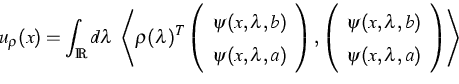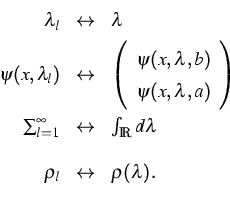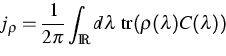Collaborator: M. Baro
,
H.-Chr. Kaiser
,
H. Neidhardt
,
J. Rehberg
Cooperation with: P. Degond, N. Ben Abdallah (Université Paul Sabatier,
Toulouse, France),
V. Zagrebnov (Université de la Méditerranée (Aix-Marseille II)
and Centre de Physique Théorique, France),
P. Exner (Academy of Sciences of the Czech Republic, Prague),
A. Jüngel (Universität Konstanz), A. Arnold (Westfälische
Wilhelms-Universität Münster)
Supported by: DFG: ``Kopplung von van Roosbroeck- und
Schrödinger-Poisson-Systemen
mit Ladungsträgeraustausch'' (Coupling between van Roosbroeck and
Schrödinger-Poisson systems
with carrier exchange)
Description:
The description of semiconductor devices by drift-diffusion models
(van Roosbroeck's system) has been
widely accepted for a long time.
Moreover, there are well-developed software packages for calculating
semiconductors based on
drift-diffusion models. However, with the developing miniaturization of
semiconductor devices
less and less atoms are involved in the processes inside many devices
with the consequence that
quantum effects become more and more important.
Hence, one has to
improve the classical drift-diffusion description taking quantum effects
at least partially into account. It would be more
correct to use a complete quantum mechanical
description of semiconductors right from the beginning; however, at present
it is not possible to handle such a description numerically.
Therefore one has
to look for a
model which uses a
drift-diffusion description in regions where this is recommended
and a quantum mechanical one in regions where quantum effects are
dominating, for instance, in the active
zone of a laser. Both descriptions seem to be incompatible.
From the physical point of view it
would be desirable to have at least a
continuity of the current densities at the interface between the two
subregions.
This leads to the necessity to consider
open quantum systems which are,
in contrast to closed quantum systems, not yet
well developed.
Considering current coupled models
one has at first to find open boundary
conditions for the Schrödinger operator.
In [6, 7], the proposal was made to use for this purpose the
Schrödinger operators with
non-selfadjoint boundary conditions
which in application to a one-dimensional Schrödinger operator H
| 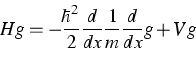 |
(1) |
on the interval ![${\Omega}:= [a,b] \subseteq \mathbb{R}$](img37.gif) , looks like
, looks like
| 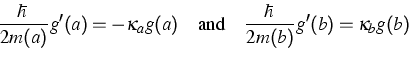 |
(2) |
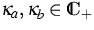 . Non-selfadjoint Schrödinger operators
of the above type and for higher spatial dimensions
have been investigated in [2].
In contrast to self-adjoint boundary conditions, which are used in case of
closed Schrödinger-Poisson systems,
one has to redefine the carrier and current densities.
The best way to find suitable definitions is to close
the open system since in this case the definitions are clear. In
[5], the minimal self-adjoint dilation of
H was chosen for the Hamiltonian of the covering closed system. The
minimal self-adjoint dilation
itself was explicitly constructed in [4] and investigated
there in detail. It turned out that the obtained
expression of the carrier density is a straightforward generalization of
the corresponding expression in the closed case.
Indeed, if the carrier density in the closed case is given by
. Non-selfadjoint Schrödinger operators
of the above type and for higher spatial dimensions
have been investigated in [2].
In contrast to self-adjoint boundary conditions, which are used in case of
closed Schrödinger-Poisson systems,
one has to redefine the carrier and current densities.
The best way to find suitable definitions is to close
the open system since in this case the definitions are clear. In
[5], the minimal self-adjoint dilation of
H was chosen for the Hamiltonian of the covering closed system. The
minimal self-adjoint dilation
itself was explicitly constructed in [4] and investigated
there in detail. It turned out that the obtained
expression of the carrier density is a straightforward generalization of
the corresponding expression in the closed case.
Indeed, if the carrier density in the closed case is given by
| ![\begin{displaymath}
u_{\varrho}(x) = \sum^\infty_{l=1} {\varrho}_l\vert\psi(x,{\lambda}_l)\vert^2 , \quad x \in [a,b],\end{displaymath}](img40.gif) |
(3) |
where 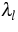 ,
, 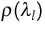 and
and 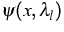 denote the eigenvalues,
the occupation numbers at the eigenvalue
denote the eigenvalues,
the occupation numbers at the eigenvalue
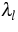 and the eigenfunction corresponding to the eigenvalue
and the eigenfunction corresponding to the eigenvalue 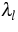 ,
respectively, then in the open case one finds
,
respectively, then in the open case one finds
| 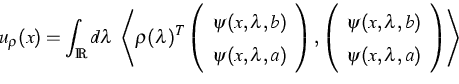 |
(4) |
where 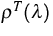 is the transposed density matrix and
is the transposed density matrix and
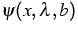 ,
, 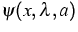 are the generalized eigenfunctions
of the dilation. Hence one has the following correspondence:
are the generalized eigenfunctions
of the dilation. Hence one has the following correspondence:
| 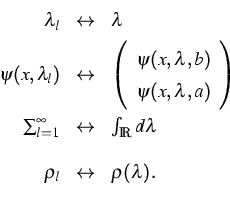 |
(5) |
The current density 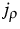 , which is always zero in the closed case, is
now constant and is, in general,
different from zero. Moreover, one gets the representation
, which is always zero in the closed case, is
now constant and is, in general,
different from zero. Moreover, one gets the representation
| 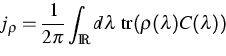 |
(6) |
where 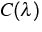 is related to the characteristic function of H.
Using the redefined notion of carrier density, a
dissipative Schrödinger-Poisson system
was considered in [3] and we have shown that
this system always has a solution. The electrostatic potential is always
bounded by a constant which is determined by the data of the problem.
The solution is in general not unique. In
[1] an attempt was made to include generation and recombination
effects into the dissipative
Schrödinger-Poisson systems.
is related to the characteristic function of H.
Using the redefined notion of carrier density, a
dissipative Schrödinger-Poisson system
was considered in [3] and we have shown that
this system always has a solution. The electrostatic potential is always
bounded by a constant which is determined by the data of the problem.
The solution is in general not unique. In
[1] an attempt was made to include generation and recombination
effects into the dissipative
Schrödinger-Poisson systems.
References:
- M. BARO, H. NEIDHARDT,
Dissipative Schrödinger-type operator as a model for
generation and recombination,
WIAS Preprint no. 737, 2002, to appear in: J. Math. Phys.
- H.-CHR. KAISER, H. NEIDHARDT, J. REHBERG,
Macroscopic current induced boundary conditions for Schrödinger-type
operators, WIAS Preprint no. 650, 2001,
to appear in: Integral Equations Operator Theory.
- M. BARO, H.-CHR. KAISER, H. NEIDHARDT, J. REHBERG,
Dissipative Schrödinger-Poisson systems, WIAS Preprint
no. 719, 2002.
- H.-CHR. KAISER, H. NEIDHARDT, J. REHBERG,
On 1-dimensional dissipative Schrödinger-type operators, their
dilations and eigenfunction expansions,
WIAS Preprint no. 664, 2001, to appear in: Math. Nachr.
-
 ,
Density and current of a dissipative Schrödinger operator,
J. Math. Phys., 43 (2002), pp. 5325-5350.
,
Density and current of a dissipative Schrödinger operator,
J. Math. Phys., 43 (2002), pp. 5325-5350.
- H.-CHR. KAISER, J. REHBERG,
About a one-dimensional stationary Schrödinger-Poisson system with
Kohn-Sham potential,
Z. Angew. Math. Phys., 50 (1999), pp. 423-458.
-
 ,
About a stationary Schrödinger-Poisson system with Kohn-Sham
potential in a bounded two- or three-dimensional domain,
Nonlinear Anal., 41A (2000), pp. 33-72.
,
About a stationary Schrödinger-Poisson system with Kohn-Sham
potential in a bounded two- or three-dimensional domain,
Nonlinear Anal., 41A (2000), pp. 33-72.
LaTeX typesetting by I. Bremer
5/16/2003
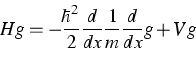
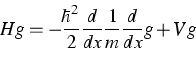
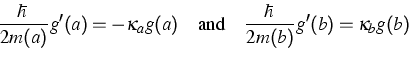
![\begin{displaymath}
u_{\varrho}(x) = \sum^\infty_{l=1} {\varrho}_l\vert\psi(x,{\lambda}_l)\vert^2 , \quad x \in [a,b],\end{displaymath}](img40.gif)