Simulation of the modulation response of

Description: In cooperation with the company MergeOptics GmbH the electrical, thermal, optical and dynamical behavior of strained multi-quantum-well (SMQW) lasers was simulated for improving their performance. The simulations were carried out using the device simulator WIAS-TeSCA based on a drift-diffusion model which is self-consistently coupled to a heat-flow equation (see [1]) and to equations for the optical field. The main goal was the optimization of the modulation response of such lasers. For this purpose details of the structure (e.g., number of quantum wells, thickness of waveguides) and the doping were varied.

Methods and results are demonstrated here for some fictive edge-emitting ridge waveguide (RW) laser. The most important part of its transverse cross section is shown in Figure 1, the simulated P-I characteristic in Figure 2. Besides RW lasers we investigated also buried heterostructure lasers in more detail.

Fig. 1: Part of the transverse cross section of a RW-SMQW laser consisting of different materials M1, M2, and so on. There are also shown isolines of the power distribution of the fundamental optical mode.
$\ProjektEPSbildNocap {0.4\linewidth}{fb02_fig1_hue_1.eps.gz} \begin{imagesonly} \addtocounter{projektbild}{-1}\end{imagesonly}$

Fig. 2: P-I characteristic of the laser. The modulation response was computed in four operating points as marked in the figure.
$\ProjektEPSbildNocap {0.4\linewidth}{fb02_fig1_hue_2} \begin{imagesonly} \addtocounter{projektbild}{-1}\end{imagesonly}$

We describe two methods for the calculation of the modulation response. The first one is the AC analysis (small signal analysis in the frequency domain). Here WIAS-TeSCA computes complex amplitudes $\widehat I(\omega)$ , $\widehat P(\omega)$ corresponding to a small harmonic modulation of the bias voltage with angular frequency $\omega$ and amplitude $\Delta U$ ( $\Delta U=0.05$ mV). The complex response function is then given by $H(\omega)=\widehat P(\omega)/\widehat I(\omega)$ , or in a normalized form by $H_n(\omega)=H(\omega)/H(0)$ . The squared modulus of H_n is seen in Figure 4. An excellent fit of H_n can be obtained according to the formula

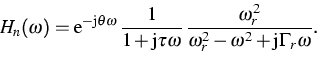$\begin{displaymath} H_n(\omega)=\text{e}^{-\text{j}\theta\omega}\,\frac{1}{1+\te... ... \frac{\omega_r^2}{\omega_r^2-\omega^2+\text{j}\Gamma_r\omega}.\end{displaymath}$

(1)

Fig. 3: Complex response functions $H_n(\omega)$ . The symbols are results obtained by small-signal analysis while the lines are computed with (1) using extracted parameters as plotted in Fig. 5.
$\ProjektEPSbildNocap {.65\linewidth}{fb02_fig1_hue_7} \begin{imagesonly} \addtocounter{projektbild}{-1}\end{imagesonly}$

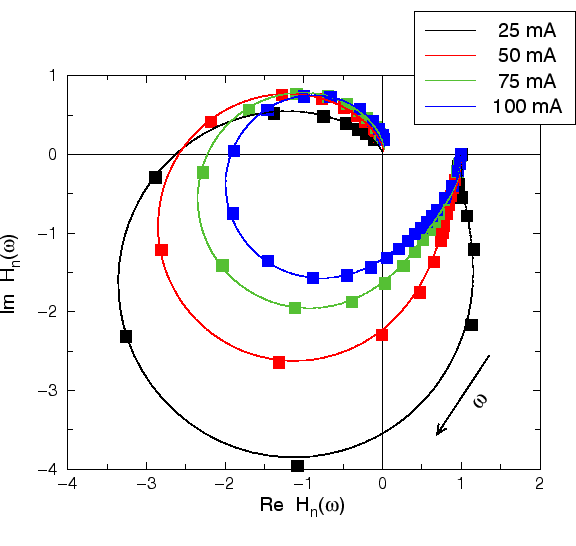
The last factor in (1) is well known from rate equation models (see [2]). The second factor is a low-pass filter while the first one describes some time delay. Both terms are due to parasitic effects, especially to the drift-diffusion transport through the device (see [3], too). The result of the fit is demonstrated in Figure 3. The extracted parameters $f_{r}=\omega_{r}/2\pi$ , $\Gamma_r$ , $\tau$ and $\theta$ are presented in a more suitable form in Figure 5. The frequency $f_{\text{3dB}}=\omega_{\text{3dB}}/2\pi$ is also shown there where $\omega_{\text{3dB}}$ solves the equation $\vert H_n(\omega_{\text{3dB}})\vert^2=1/2$ .Let us note that a fit without using the parasitic terms gives insufficient results.

Fig. 4: Simulation results obtained by small-signal analysis in the frequency domain (left) and by pulse excitation in the time domain (right)
$\makeatletter \@ZweiProjektbilderNocap[h]{0.48\linewidth}{fb02_fig1_hue_3.eps}{fb02_fig1_hue_4.eps} \makeatother$

Fig. 5: Extracted parameters $f_{r}^{\,2}$ , $f_{\text{3dB}}^{\,2}$ (left) and $\Gamma_r$ , $\tau^{-1}$ , $(2\pi\theta)^{-1}$ (right)
$\makeatletter \@ZweiProjektbilderNocap[h]{0.48\linewidth}{fb02_fig1_hue_5.eps}{fb02_fig1_hue_6.eps} \makeatother$

The second method is a current-driven transient simulation where a short rectangular pulse is added to the injection current ( $\Delta I(t)=0.1$ mA, $0\le t \le 0.02\; \text{ns}$ ). WIAS-TeSCA computes corresponding variations of the output power $\Delta P(t)$ which are seen in the right-hand side of Figure 4 for $t \ge 0.02 \;\text{ns}$ (to enhance clearness the result for I=75 mA was omitted here). Corresponding to (1) the functions $\Delta P$ were fitted according to the formula

$\begin{displaymath} \Delta P(t)=c_1\,\text{e}^{-t/\tau}+ c_2 \,\text{cos}(\omega... ...\delta)\, \text{e}^{-\Gamma_r t/2},\quad t\ge 0.02 \;\text{ns},\end{displaymath}$

(2)

where $\omega_0^2=\omega_r^2-\Gamma_r^2/4$ , and c₁, c₂, $\delta$ depend on $\omega_r$ , $\Gamma_r$ , $\tau$ , $\theta$ . The parameters extracted in this manner coincide well with the values found by the first method, and with (1) nearly the same frequency response functions as on the left hand side of Figure 4 are obtained. But let us note that this method requires very small time steps in order to get correct results.

Simulation of the modulation response of strained multi-quantum-well lasers