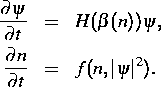
|
|
|
[Contents] | [Index] |
Kooperation: V. Tronciu (Technische Universität Moldawien), H.-P. Nolting, B. Sartorius, D. Hoffmann (Heinrich-Hertz-Institut für Nachrichtentechnik (HHI) Berlin), H.-J. Wünsche (Institut für Physik, HU Berlin), L. Recke (Institut für Mathematik, HU Berlin), H. Wenzel (Ferdinand-Braun-Institut für Höchstfrequenztechnik, Berlin)
Beschreibung der Forschungsarbeit:
Die Untersuchung von nichtlinearen dynamischen Effekten in DFB-Halbleiterlasern ist ein zentrales, längerfristiges Projekt der Forschungsgruppe. Bearbeitet wird dabei ein breites Spektrum von Fragestellungen, das sowohl das grundlegende mathematische Verständnis der auftretenden Modelle, die problemangepasste Modellierung als auch die Simulation und Optimierung bei der Entwicklung von konkreten Bauelementen betrifft, die von den Kooperationspartnern am HHI durchgeführt wird. Dort wird versucht, kompliziertes nichtlineares Verhalten (Synchronisation, hochfrequente Selbstpulsation, schnelles Schalten) von DFB-Mehrsektionslasern für den Einsatz in Bauelementen zur rein optischen Datenverarbeitung und Signalregeneration nutzbar und beherrschbar zu machen. Ausgangspunkt für unsere Untersuchungen zur zeitlichen Dynamik von DFB-Mehrsektionslasern sind die folgenden Modellgleichungen
Dabei beschreibt der komplexe Vektor
![]() das
longitudinale zeitliche Verhalten der vorwärts- bzw.
rückwärtslaufenden optischen Welle; der lineare hyperbolische Operator
das
longitudinale zeitliche Verhalten der vorwärts- bzw.
rückwärtslaufenden optischen Welle; der lineare hyperbolische Operator
![]() modelliert die Wellenausbreitung, Lichtverstärkung und interne
Kopplung am Bragg-Gitter.
Die Ladungsträger n(t,z) sind nichtlinear an das optische Feld
gekoppelt und können sowohl gemittelt über einzelne Sektionen als
auch räumlich aufgelöst betrachtet werden.
modelliert die Wellenausbreitung, Lichtverstärkung und interne
Kopplung am Bragg-Gitter.
Die Ladungsträger n(t,z) sind nichtlinear an das optische Feld
gekoppelt und können sowohl gemittelt über einzelne Sektionen als
auch räumlich aufgelöst betrachtet werden.
Die Reflexion an den Facetten des Lasers sowie ein möglicher optischer Input a(t) werden durch geeignete Randbedingungen der Gestalt
berücksichtigt, wobei r0 und r1 komplexe Reflexionskoeffizienten sind.
Bezüglich der Modellgleichungen (1), (2) wurden folgende Untersuchungen durchgeführt:
Im Folgenden werden die erhaltenen Resultate kurz beschrieben.
Lösbarkeit des Anfangs-Randwertproblems für die Modellgleichungen (1), (2).
Das hyperbolische Gleichungssystem (1) wurde bisher nur mit sektionsweise gemittelten Ladungsträgerdichten analytisch auf seine Lösbarkeit untersucht. Mathematisch bewirkt dieser Mittelungsprozess eine erhebliche Vereinfachung des Existenzbeweises für eine Lösung.
Gegenstand der analytischen Untersuchungen waren Systeme (1), (2), bei denen auch zeitlich unstetige optische Inputs a(t) und Ströme I(t) zugelassen werden. Dies macht es erforderlich, ein geeignetes Konzept schwacher Lösungen einzuführen. Diese Lösungen erfüllen die zu (1) gehörende Integralgleichung nur im schwachen Sinne und die zweite Randbedingung in (2) nur in der aufintegrierten Form:
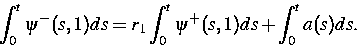
Das Differentialgleichungssystem (1) wurde in der folgenden abstrakten Form untersucht:
Dabei ist ![]() ein komplexer Vektor,
ein komplexer Vektor, ![]() ein reeller Vektor und
ein reeller Vektor und ![]() ein kleiner Parameter;
die Matrizen Gi (n) sind hermitesch und positiv definit. Diese
Gleichungen können als abstrakte Lasergleichungen mit linearer Optik,
etwa im Sinne einer Galerkin-Approximation von (1),
angesehen werden. Für (3) wurde gezeigt, dass alle
Lösungen, deren Ausgangsleistung durch
ein kleiner Parameter;
die Matrizen Gi (n) sind hermitesch und positiv definit. Diese
Gleichungen können als abstrakte Lasergleichungen mit linearer Optik,
etwa im Sinne einer Galerkin-Approximation von (1),
angesehen werden. Für (3) wurde gezeigt, dass alle
Lösungen, deren Ausgangsleistung durch ![]() charakterisiert wird, die also
vergleichbar mit der der stationären Lösung sind, in einer kleinen
Umgebung einer kritischen Fläche liegen,
deren n-Koordinate die Eigenschaft aufweist, dass
charakterisiert wird, die also
vergleichbar mit der der stationären Lösung sind, in einer kleinen
Umgebung einer kritischen Fläche liegen,
deren n-Koordinate die Eigenschaft aufweist, dass ![]() mindestens einen Eigenwert auf der imaginären Achse besitzt. Aus
Stabilitätsgründen konzentrieren wir uns nur auf den Teil der
kritischen Fläche, wir bezeichnen sie als Schwellenfläche, wo
mindestens einen Eigenwert auf der imaginären Achse besitzt. Aus
Stabilitätsgründen konzentrieren wir uns nur auf den Teil der
kritischen Fläche, wir bezeichnen sie als Schwellenfläche, wo
![]() keine Eigenwerte mit positivem Realteil besitzt. Falls
m die Anzahl der Eigenwerte auf der imaginären Achse darstellt,
wird
die Existenz einer attrahierenden
(2m+k)-dimensionalen invarianten Mannigfaltigkeit in der
Nähe der Schwellenfläche gezeigt, d. h. nur
m Komponenten von
keine Eigenwerte mit positivem Realteil besitzt. Falls
m die Anzahl der Eigenwerte auf der imaginären Achse darstellt,
wird
die Existenz einer attrahierenden
(2m+k)-dimensionalen invarianten Mannigfaltigkeit in der
Nähe der Schwellenfläche gezeigt, d. h. nur
m Komponenten von ![]() können in diesem Fall essentiell von null
verschieden sein. Im Allgemeinen ist die Anzahl m der kritischen Moden
klein, so dass das erwähnte Resultat die Modellierung
von Lasergleichungen mit nur einer geringen Anzahl von optischen Moden
rechtfertigt. Im generischen Fall ist m=1, und wir können zeigen,
dass die Existenz von Parameterregimen mit Selbstpulsationen hier sehr
unwahrscheinlich ist (das entsprechende Parametergebiet ist
von der Größenordnung
können in diesem Fall essentiell von null
verschieden sein. Im Allgemeinen ist die Anzahl m der kritischen Moden
klein, so dass das erwähnte Resultat die Modellierung
von Lasergleichungen mit nur einer geringen Anzahl von optischen Moden
rechtfertigt. Im generischen Fall ist m=1, und wir können zeigen,
dass die Existenz von Parameterregimen mit Selbstpulsationen hier sehr
unwahrscheinlich ist (das entsprechende Parametergebiet ist
von der Größenordnung ![]() ). Es konnte weiterhin
nachgewiesen werden, dass mit mehreren kritischen Moden (m=2), oder
wenn ein
einzelner kritischer Eigenwert
die imaginäre Achse
nicht generisch kreuzt,
wesentlich bessere Aussichten für das
Auftreten von Selbstpulsationen bestehen, da in diesem Fall das
entsprechende Gebiet im Parameterraum von der Größenordnung
). Es konnte weiterhin
nachgewiesen werden, dass mit mehreren kritischen Moden (m=2), oder
wenn ein
einzelner kritischer Eigenwert
die imaginäre Achse
nicht generisch kreuzt,
wesentlich bessere Aussichten für das
Auftreten von Selbstpulsationen bestehen, da in diesem Fall das
entsprechende Gebiet im Parameterraum von der Größenordnung
![]() ist ([6]).
ist ([6]).
Modellierung des passiven dispersiven Reflektors im Rahmen der
Einmodenapproximation.
Betrachtet man Laser mit nur einer aktiven
Sektion und reduziert das System (1) auf die dominante
Mode von ![]() , so erhält man ein reelles zweidimensionales System
gewöhnlicher Differentialgleichungen
, so erhält man ein reelles zweidimensionales System
gewöhnlicher Differentialgleichungen
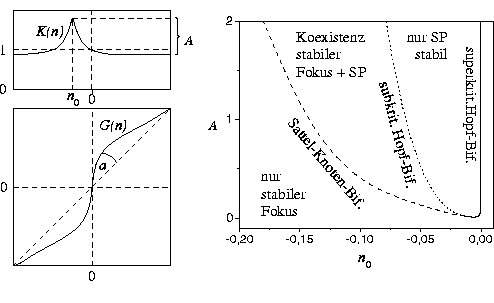
für die skalierte optische Leistung p der ausgewählten Mode und die skalierte gemittelte Ladungsträgerdichte n in der aktiven Sektion (die Schwelldichte wurde in den Ursprung verschoben, so dass G(0)=0 gilt). Die Eigenschaften der als dispersiver Reflektor agierenden passiven Lasersektion gehen in dieses System nur durch die Funktionen G(n) und K(n) ein. Im Einsektionslaser gilt G(n)=n und K(n)=1.
Der dispersive Reflektor bewirkt typischerweise eine
Lorentz-artige Resonanz in K und eine Änderung ![]() des Anstiegs von G(n) in . Dieser Zugang gestattet, die
Dynamik im System (4), (5)
in Abhängigkeit von
des Anstiegs von G(n) in . Dieser Zugang gestattet, die
Dynamik im System (4), (5)
in Abhängigkeit von ![]() sowie der Position n0 und der
Höhe A der Resonanz von K(n) (siehe Bilder auf der linken Seite in
Abb. 1) zu untersuchen (siehe [1]).
Die Resultate der numerischen Bifurkationsanalyse sind im
Bifurkationsdiagramm im rechten Bild in Abb.
1 dargestellt.
sowie der Position n0 und der
Höhe A der Resonanz von K(n) (siehe Bilder auf der linken Seite in
Abb. 1) zu untersuchen (siehe [1]).
Die Resultate der numerischen Bifurkationsanalyse sind im
Bifurkationsdiagramm im rechten Bild in Abb.
1 dargestellt.
 |
Die dargestellten Bifurkationsszenarien wurden auch in den
Simulationen des Modells
(1) beobachtet (siehe
Jahresforschungsbericht
1998
).
Weiteres Ziel der
Untersuchungen war die Frequenz der Selbstpulsationen. Es wurde
festgestellt, dass diese Frequenz nicht nur durch den Pumpstrom (siehe
Jahresforschungsbericht 1998
),
sondern auch durch ![]() erhöht werden kann.
erhöht werden kann.
Hauptgegenstand unserer Modellierung sind Laser, die aus zwei DFB-Sektionen (Gainsektion, Reflektorsektion) und einer Fabry-Perot-Sektion (Phasensektion) bestehen. Die Reflektorsektion wird so gepumpt, dass sie im Wesentlichen als passiver Reflektor dient. Eine geeignete Wahl des Pumpstromes in der Phasensektion führt zu DQS-Selbstpulsationen des Lasers. Das Ziel der numerischen Untersuchungen besteht darin, durch geeignete Wahl der Laser-Parameter robuste DQS-Selbstpulsationen mit hoher Frequenz zu erzielen.
a. Modellvereinfachungen.
Das im Folgenden verwendete Modell erhalten wir aus (1),
(2), indem wir für ![]() in den einzelnen Sektionen
die folgenden Ausdrücke verwenden:
in den einzelnen Sektionen
die folgenden Ausdrücke verwenden:
Dabei bedeutet |Lp| die Länge der Phasensektion, ![]() beschreibt den Verlust in den einzelnen Sektionen, n stellt die
räumlich gemittelte Ladungsträgerdichte in der Gainsektion dar.
beschreibt den Verlust in den einzelnen Sektionen, n stellt die
räumlich gemittelte Ladungsträgerdichte in der Gainsektion dar.
Dieses vereinfachte Modell vernachlässigt die Dynamik der Ladungsträger in Phasensteuerungs- und Reflektorsektion, sie dienen als passiver dispersiver Reflektor (PDR) für die Gainsektion.
Die numerischen Resultate der nächsten Abschnitte wurden sowohl für das vollständige als auch für das PDR-Modell erhalten.
Um Selbstpulsationen zu erhalten, muss die folgende relative Lage der
Reflexionsspektren von Gain- (durchgezogene Kurve) und
Reflektorsektionen (punktierte Kurve) durch geeignete Wahl des
Detuning ![]() (siehe linkes Bild in Abb.
3) erhalten werden.
(siehe linkes Bild in Abb.
3) erhalten werden.
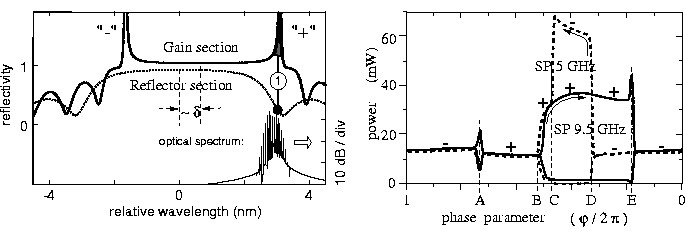 |
Die dünne durchgezogene Linie im linken Bild stellt das optische Spektrum des Outputs an der
Facette der Lasersektion dar.
Die Zeichen ,,+`` und ,,-`` markieren, ob die langwellige oder die
kurzwellige DFB-Mode der Gainsektion dominant ist. Wie im Bild gezeigt, muss
die ,,+``-Mode mit einer abklingenden Flanke des Spektrums der
Reflektorsektion übereinstimmen.
In diesem Fall kann durch Anpassen des Phasenparameters ![]() eine
Selbstpulsation gefunden werden, wie im rechten Bild von Abb.
3 zu sehen ist.
Die durchgezogene Linie (
eine
Selbstpulsation gefunden werden, wie im rechten Bild von Abb.
3 zu sehen ist.
Die durchgezogene Linie (![]() von nach
von nach ![]() variiert) und die
gestrichelte Linie (
variiert) und die
gestrichelte Linie (![]() von
von ![]() nach variiert) stellen entweder
den stationären Output oder Maximum und Minimum während einer Periode der
Selbstpulsation dar.
In allen Fällen, ausgenommen der Punkt A,
ist eine Mode deutlich dominant. ,,+``
bzw. ,,-`` über den Linien markieren, ob die langwellige oder die kurzwellige
Mode der Gainsektion aktiv ist.
Das große
Intervall (
nach variiert) stellen entweder
den stationären Output oder Maximum und Minimum während einer Periode der
Selbstpulsation dar.
In allen Fällen, ausgenommen der Punkt A,
ist eine Mode deutlich dominant. ,,+``
bzw. ,,-`` über den Linien markieren, ob die langwellige oder die kurzwellige
Mode der Gainsektion aktiv ist.
Das große
Intervall (![]() ) mit DQS-Selbstpulsationen wird für
fallendes
) mit DQS-Selbstpulsationen wird für
fallendes ![]() (im Bild von links nach rechts)
beobachtet. Das entspricht steigendem Pumpstrom in der
Phasensteuerungssektion.
Bei steigendem
(im Bild von links nach rechts)
beobachtet. Das entspricht steigendem Pumpstrom in der
Phasensteuerungssektion.
Bei steigendem ![]() beobachten wir DQS-Selbstpulsationen nur im Intervall
beobachten wir DQS-Selbstpulsationen nur im Intervall
![]() . Gleichzeitig treten DQS-Selbstpulsationen eines
anderen Typs
auf der ,,-``-Mode im Intervall
. Gleichzeitig treten DQS-Selbstpulsationen eines
anderen Typs
auf der ,,-``-Mode im Intervall ![]() auf.
Dieses Verhalten der Lösung wird dadurch erklärt, dass die ,,-``-Mode starkes
Feedback vom Reflektor (siehe linkes Bild in Abb. 3)
bekommt.
auf.
Dieses Verhalten der Lösung wird dadurch erklärt, dass die ,,-``-Mode starkes
Feedback vom Reflektor (siehe linkes Bild in Abb. 3)
bekommt.
Zu diesem Zweck führen wir die statische Verstimmung ![]() zwischen den
beiden DFB-Gittern als Design-Parameter ein (siehe [4]).
Dieses Herangehen
ist durch die Beobachtung motiviert, dass die nicht pulsierende ,,-``-Mode
(Bild links in Abb. 3) ein stärkeres Feedback von der
Reflektorsektion erhält als die pulsierende ,,+``-Mode. Wir erwarten,
dass das Parametergebiet, in dem Selbstpulsationen auftreten, durch
Verminderung des Feedbacks für die nicht pulsierende Mode, z. B. durch
geeignete Gitterverstimmung, vergrößert wird.
Um diese Hypothese zu überprüfen, wurde der Verstimmungsparameter
zwischen den
beiden DFB-Gittern als Design-Parameter ein (siehe [4]).
Dieses Herangehen
ist durch die Beobachtung motiviert, dass die nicht pulsierende ,,-``-Mode
(Bild links in Abb. 3) ein stärkeres Feedback von der
Reflektorsektion erhält als die pulsierende ,,+``-Mode. Wir erwarten,
dass das Parametergebiet, in dem Selbstpulsationen auftreten, durch
Verminderung des Feedbacks für die nicht pulsierende Mode, z. B. durch
geeignete Gitterverstimmung, vergrößert wird.
Um diese Hypothese zu überprüfen, wurde der Verstimmungsparameter ![]() über einen 15 nm großen Bereich variiert. Für jedes
über einen 15 nm großen Bereich variiert. Für jedes ![]() wurde der
Phasenwinkel
wurde der
Phasenwinkel ![]() abwärts geändert, von
abwärts geändert, von ![]() bis .
Die Regionen mit DQS-Selbstpulsationen sind im oberen Bild von Abb.
4 als weiße Inseln mit dicken
bis .
Die Regionen mit DQS-Selbstpulsationen sind im oberen Bild von Abb.
4 als weiße Inseln mit dicken
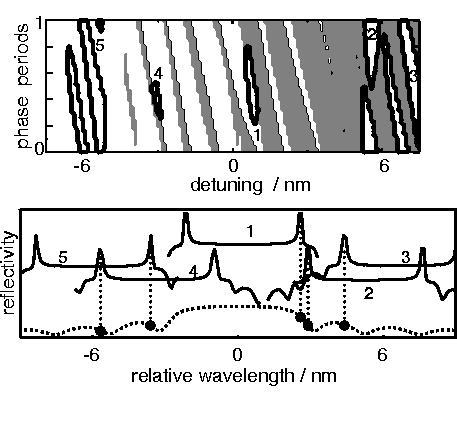 |
schwarzen Rändern eingezeichnet. Insel 1 in der Mitte und die Selbstpulsationen darin entsprechen der Situation in Abb. 3. Graue und weiße Gebiete außerhalb der Inseln zeigen an, ob die kurzwellige oder die langwellige Mode aktiv ist.
Der untere Teil von Abb. 4 stellt die Feedback-Spektren der Reflektorsektion (gepunktet) und der Gainsektion (durchgezogen) für die verschiedenen zu Pulsationsinseln gehörenden Verstimmungen dar. Die gestrichelten vertikalen Linien zeigen an, welche der DFB-Moden der Gainsektion jeweils aktiv ist.
Bemerkenswert ist, dass es Phasenparameter gibt, für die die Gainsektionsmode mit betragsmäßig deutlich kleinerem Feedback dominiert. Im oberen Teil des Bildes erkennt man die Sprünge zur Mode mit kleinerem Feedback als schmale Streifen (Wechsel zwischen grau und weiß) im Bereich mit moderatem Detuning. Bei großem Detuning, d. h. dort, wo diese Modensprünge vollständig verschwinden, wurden, wie erwartet, neue große Selbstpulsationsinseln entdeckt.
Projektliteratur:
|
|
|
[Contents] | [Index] |