SPP 1748 Logo

DFG Priority Programme 1748:
Reliable Simulation Techniques in Solid Mechanics. Development of Non-standard Discretisation Methods, Mechanical and Mathematical Analysis

Subproject BV-FEM:
Finite element approximation of functions of bounded variation
and application to models of damage, fracture, and plasticity



Project Head: Dr. Marita Thomas (in collaboration with Prof. Dr. Sören Bartels, U Freiburg)
Investigator: Marijo Milicevic
Funding period: October, 2014 - September, 2017


Description


The aim of this project is to establish reliable and efficient numerical methods for models of solids with spatial discontinuities caused by the evolution of dissipative processes such as plasticification, damage or fracture. In particular, the project focuses on such prototypical models that use the class of BV-functions to mathematically describe the discontinuities, that are guaranteed to converge to a solution of the infnite-dimensional model and for which iterative solution methods can be constructed. Emphasis is on unregularized numerical approaches that lead to sharp approximations of discontinuities on coarse grids and rigorous convergence proofs. Some typical and guiding principles can be seen in the following examples:
  • A hardening regularization of perfectly plastic materials leads to a strong regularization of shear bands:

    PIC1

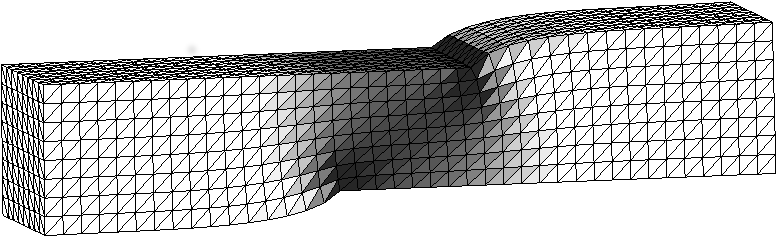
    (Figure from: S. Bartels, Numerical methods for nonlinear partial differential equations, Springer Series in Computational Mathematics, 47, Springer, 2015.)


  • local, adaptive refinement strategies allow accurate approximations of discontinuities:

    PIC2

    (Figure from: S. Bartels: Error control and adaptivity for a variational model problem defined on functions of bounded variation,
    Math. Comp. (accepted))


  • subdifferential flows define discontinuous evolutions:

    PIC3 PIC4

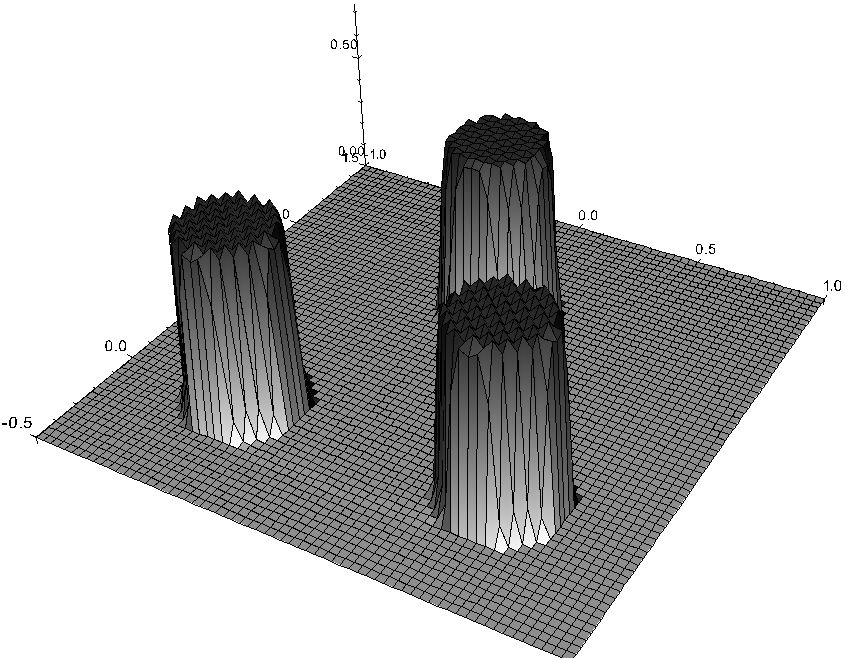
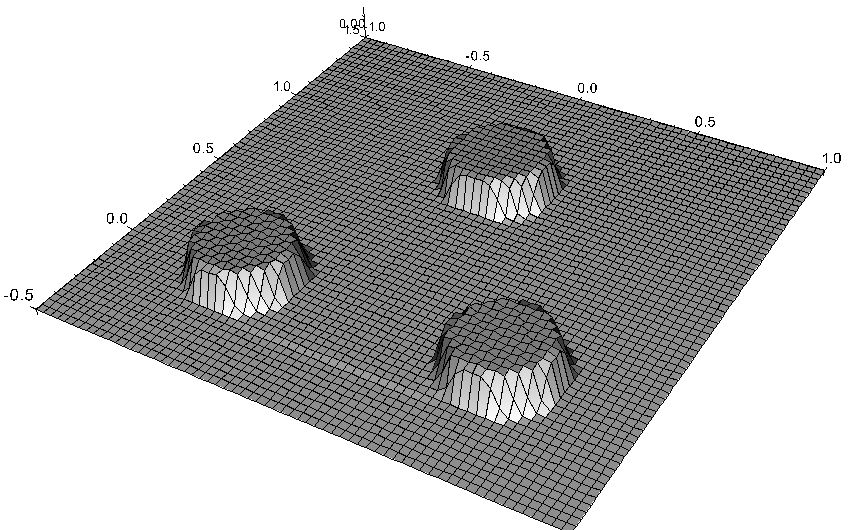
    (Figure from: S. Bartels, R. H. Nochetto, and A. J. Salgado: Discrete total variation flows without regularization.
    SIAM J. Numer. Anal. 52(1), 363-385, 2014.)

The main objectives of the research project are the development, analysis, and implementation of finite element methods for model problems describing discontinuities in BV. This includes the derivation of a priori and a posteriori error estimates as well as the construction of adaptive and extended approximation methods for BV-prototype models such as the Rudin-Osher-Fatemi and the Mumford-Shah model.

The techniques will be transferred to analytically justified and closely related models for the description of rate-independent inelastic processes, in particular perfect plasticity, damage and fracture. The methods and results will be applied to particular model scenarios and benchmark problems in mechanics.



Publications




Events



Preliminary Work


  • M. Thomas: Uniform Poincaré-Sobolev and relative isoperimetric inequalities for classes of domains.
    To appear in Discrete Continuous Dynamical Systems, Series A 35:2741--2761, 2015. (WIAS Preprint 1797)
  • R. Rossi and M. Thomas: From an adhesive to a brittle delamination model in thermo-visco-elasticity.
    ESAIM Control Optim. Calc. Var., 21:1--59, 2015. (WIAS Preprint 1692)
  • M. Thomas: Quasistatic damage evolution with spatial BV-regularization. DCDS-S 6:235--255, 2013, AIMS. (WIAS Preprint 1638)
  • T. Roubíček, M. Thomas and C. Panagiotopoulos: Stress-driven local solution approach to quasistatic brittle delamination.
    Nonlinear Analysis: Real World Applications 22(2015)645-663. (WIAS Preprint 1889)
  • A. Mielke, T. Roubíček and M. Thomas: From Damage to Delamination in Nonlinearly Elastic Materials at Small Strains,
    J. of Elasticity, 109(2):235--273, 2012, Springer. (WIAS Preprint 1542)
  • P. Gruber, D. Knees, S. Nesenenko and M. Thomas: Analytical and numerical aspects of time-dependent models with internal variables, ZAMM Z. Angew. Math. Mech., 90 (2010) pp. 861--902. (WIAS Preprint 1460)
  • M. Thomas and A. Mielke: Damage of nonlinearly elastic materials at small strain --- Existence and regularity results,
    ZAMM Z. Angew. Math. Mech., 90 (2010) pp. 88--112. (WIAS Preprint 1397)
  • S. Bartels: Error control and adaptivity for a variational model problem defined on functions of bounded variation,
    Math. Comp. 84(293):1217--1240,2015.
  • S. Bartels: Total variation minimization with finite elements: convergence and iterative solution,
    SIAM J. Numer. Anal., 50(3):1162--1180, 2012.
  • S. Bartels: Broken Sobolev space iteration for total variation regularized problems.
    IMA Journal of Numerical Analysis 36(2):493, 2016.
  • S. Bartels: Quasi-optimal error estimates for implicit discretizations of rate-independent evolutions,
    SIAM J. Numer. Anal. 52(2), 708--716, 2014.
  • S. Bartels, A. Mielke, and T. Roubíček: Quasi-static small-strain plasticity in the limit of vanishing hardening and its numerical approximation, SIAM J. Numer. Anal., 50(2):951--976, 2012.
  • S. Bartels, R. H. Nochetto, and A. J. Salgado: Discrete total variation flows without regularization,
    SIAM J. Numer. Anal. 52(1), 363--385, 2014.
  • S. Bartels, R. H. Nochetto, and A. J. Salgado: A total variation diminishing interpolation operator and applications,
    Math. Comp. to appear 2015, available online at http://aam.uni-freiburg.de/abtlg/ls/lsbartels/publ, 2013.


Last modified: 2018-01-23 by Marita Thomas