Hang Si Research Group: Numerical Mathematics and Scientific Computing Weierstrass Institute for Applied Analysis and Stochastics (WIAS) Mohrenstr. 39 10117 Berlin, Germany si(at)wias-berlin.de I'm currently on vacation leave until August 31, 2021.

I'm a scientific staff member of the Weierstrass Institute for Applied Analysis and Stochastics (WIAS) in the research group of Numerical Mathematics and Scientific Computing.

I work in the field of automatic mesh generation, which is a topic about how to partition a geometric domain into a set of simple (non-overlapping) cells. It has wide variety of applications: mathematical modeling, computer-aided design, visualizations, and so on. It combines different topics from mathematics, computer science, and engineering. It principally requires the studies of discretizing a continuous space in both of its topology and geometry. My primary investigations are the existence and the complexity of such a discretization. Many questions of this study stem from problems in discrete and combinatorial geometry.

I'm developing the software, TetGen, which implements state-of-the-art methods and algorithms for constructing Delaunay tetrahedralizations and quality tetrahedral meshes. The primary goal of TetGen is to provide a robust and efficient meshing tool for solving practical problems in engineering.
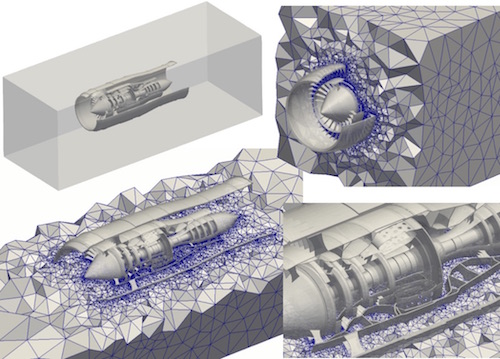
Here is an example of 3d mesh generated by TetGen.

TetGen 1.6 is released on August 31, 2020.

Here is a preprint about a geometric fact of convex prismatoids: On decomposition of embedded prismatoids in $R^3$ without additional points, WIAS Preprint No. 2602, (2019) pdf (10 Mb)

Here is a preprint about the geoemtric and combinatorial properties of the famous Lawson's flip algorithm: On monotone sequences of directed flips, triangulations of polyhedra, and structural properties of a directed flip graph, WIAS Preprint No. 2554, (2018) pdf (2.6 Mb)

For details of my current research, please take a look at the list of my publications.

I'm the co-orginizer of the 9th International Conference Numerical Geometry, Grid Generation and Scientific Computing (NUMGRID 2018), December 3-5, 2018, Moskow Russia. It is also the special event for CELEBRATING THE 150TH ANNIVERSARY OF G. F. VORONOI.

I gave a course on "Mesh Generation Methods and Softwares" in the 2018 International Summer School of Beihang University (Beijing University of Aeronautics and Astronautics), from July 9 to August 3, 2018, in Beijing. This course is suitable for senior and graduate students in engineering, computer science, and applied mathematics.

The webiste of the course is maintained at here (Lecture notes as well as source codes are available)

A program, called Detri2, is specially developed for teaching and learning together with this course.