[Next]:  Numerical analysis of complex stochastic models  
 [Up]:  Project descriptions  
 [Previous]:  Inference for complex statistical models  
 [Contents]   [Index] 

Applied mathematical finance

 

Collaborator: S. Jaschke , G.N. Milstein , O. Reiß , J. Schoenmakers , V. Spokoiny , J.-H. Zacharias-Langhans  

Cooperation with: A. Bachi (University of Twente, The Netherlands), B. Coffey (Merrill Lynch, New York, USA), J.P. Dogget (Risk Waters Group, London, UK), H. Föllmer, W. Härdle, U. Küchler, R. Stehle (Humboldt-Universität zu Berlin), H. Haaf (Münchener Rückversicherung AG, München), A.W. Heemink, H. van der Weide (Technische Universiteit, Delft, The Netherlands), P. Kloeden (Johann Wolfgang Goethe-Universität, Frankfurt am Main), J. Kremer, C. März, T. Sauder, T. Valette (Bankgesellschaft Berlin AG, Berlin), O. Kurbanmuradov (Turkmenian Academy of Sciences, Ashkhabad), M. Schweizer (Technische Universität Berlin/Universität München), G. Stahl (Bundesaufsichtsamt für das Kreditwesen), U. Wystup (Commerzbank AG, Frankfurt am Main)

Supported by: Bankgesellschaft Berlin AG, SWON Netherlands (Dutch Research Association), BMBF: ``Effiziente Methoden zur Bestimmung von Risikomaßen'' (Efficient methods for valuation of risk measures - 03SCM6B5)

Description:

The project Applied mathematical finance of the Research Group Stochastic Algorithms and Nonparametric Statistics is concerned with the stochastic modeling of financial data, the valuation of derivative instruments (options), and risk management for banks. The implementation of the developed models and their application in practice is done in cooperation with financial institutions.

Since the Basel Committee's proposal for ``An internal model-based approach to market risk capital requirements'' (1995) was implemented in national laws, banks have been allowed to use internal models for estimating their market risk and have been able to compete in the innovation of risk management methodology. Since all banks are required to hold adequate capital reserves with regard to their outstanding risks, there has been a tremendous demand for risk management solutions. These problems of risk measurement and risk modeling are the subject of the BMBF project ``Efficient methods for valuation of risk measures'', which started in January 2001 in cooperation with and with support of the Bankgesellschaft Berlin AG.

Methods for the valuation of transition densities of diffusions, or more generally, stochastic differential equations are useful in financial modeling. In joint work with the projects ``Inference for complex statistical models'' and ``Numerical methods for stochastic models'' we discovered a general root-N consistent Monte Carlo estimator for a diffusion density ([16]).

Within the SWON Netherlands project new progress has been made with respect to the unified modeling of stocks and interest rates. This was presented at RISK Europe 2001 (Paris) ([20]).

1. Risk management for financial institutions  (S. Jaschke, O. Reiß, J. Schoenmakers, V. Spokoiny, J.-H. Zacharias-Langhans).

Although the basic principles of the evaluation of market risks are now more or less settled, in practice many thorny statistical and numerical issues remain to be solved. Specifically the industry standard, the approximation of portfolio risk by the so-called ``delta-gamma normal'' approach, can be criticized because of the quadratic loss approximation and the Gaussian assumptions. Further, in the context of the ``Basel II'' consultations, fundamental questions arise in the area of Credit Risk Modeling.

In cooperation with Bankgesellschaft Berlin AG we work on a project concerning the problem of efficient valuation of complex financial instruments, for example American options and convertible bonds. For standard American options our objective was to increase the speed and accuracy of various algorithms, for example by Richardson extrapolation. Further we focused on the problem of how to incorporate credit risk in the valuation of highly complex instruments like, e.g., ASCOTs (Asset Swapped Convertible Option Transactions). The close cooperation with traders in the bank proved to be very fruitful in testing and comparing several models that combine credit and market risk.


 
Fig. 1: A graphical analysis of a convertible bond. The different colors indicate different exercise strategies of call and put options.
%% \ProjektEPSbildNocap {10cm}{bmbf_ffm_convertible_call2.eps}

In preparation of the lecture ``Risk Management for Financial Institutions'', given by Stefan Jaschke in the winter terms 2000/01 and 2001/02, an extensive review of the general literature on the subject was done. The practical implementation of an enterprise-wide risk management system needs an understanding of the economic, statistical, numerical, social, and information technology aspects of the problem. The insights gained from the study of the general literature allow to assess not only the inner-mathematical relevancy, but also the practical relevancy of new ideas and open problems.

One of the problems that arose in the consulting with Bankgesellschaft Berlin led to a study of the Cornish-Fisher approximation in the context of delta-gamma-normal approximations ([10]). An overview of the approximation methods in the context of delta-gamma-normal models was given by [13].

The relation between coherent risk measures , valuation bounds, and certain classes of portfolio optimization problems was established in [12]. One of the key results is that coherent risk measures are essentially equivalent to generalized arbitrage bounds, also called ``good deal bounds'' by Cerny and Hodges. The results are economically general in the sense that they work for any cash stream spaces, be it in dynamic trading settings, one-step models, or deterministic cash streams. They are also mathematically general as they work in (possibly infinite-dimensional) linear spaces. The valuation theory seems to fill a gap between arbitrage valuation on the one hand and utility maximization (or equilibrium theory) on the other hand. Coherent valuation bounds strike a balance in that the bounds can be sharp enough to be useful in the practice of pricing and still be generic, i.e. somewhat independent of personal preferences, in the way many coherent risk measures are somewhat generic. Coherent risk measures are so important because of the deficiencies of the currently used quantile-VaR, which is not coherent. These deficiencies of quantile-VaR as a risk measure are discussed and contrasted with the properties of coherent risk measures in [11], which was submitted to the Basel Committee in the consultation period of the ``Basel II'' proposal. Generalizations of coherent risk measures are currently being studied by S. Jaschke and P. Mathé.

In the context of the BMBF project ``Efficient methods for valuation of risk measures'' we concentrated on the problem of estimating the Value-at-Risk  for large portfolios by full Monte Carlo valuation. In this respect we closely work together with the project ``Numerical methods for stochastic models''. In order to obtain fairly accurate results by this method in acceptable time, variance reduction techniques like importance sampling or stratified sampling have to be used ([7]). To apply these techniques one typically needs some a priori estimation of the value to be determined. The industrial standard delta-gamma-normal approximation poses, while being standard, computational problems which demand careful analysis. We developed well-adapted algorithms for the generalized eigenvalue problem and for the Fourier inversion arising in this context.

2. Interest rate modeling , calibration, and pricing of non-standard derivatives (G.N. Milstein, O. Reiß, J. Schoenmakers).      

Previously we established a conceptual approach of deriving parsimonious correlation structures suitable for the implementation in the LIBOR/EurIBOR market model  given by

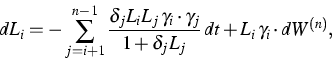
\begin{eqnarray*} dL_i=-\sum_{j=i+1}^{n-1}\frac{\delta_jL_iL_j\, \gamma_i\cdot\gamma_j}{1+\delta_jL_j}\,dt +L_i\,\gamma_i\cdot dW^{(n)},\end{eqnarray*}

where the LIBOR/EurIBOR processes Li are defined in [t0,Ti] with $\delta_i=T_{i+1}-T_i$ being day count fractions and $\gamma_i$ = $(\gamma_{i,1},\ldots,\gamma_{i,d})$ deterministic volatility functions. Further, $(W^{(n)}(t)\mid t_0\leq$ $t\leq T_{n-1})$ is a d-dimensional Wiener process under the so-called terminal measure $\mbox{$\rm{I\!P}$}_n.$By imposing additional constraints on a known ratio correlation structure, motivated by economically sensible assumptions concerning forward LIBOR/EurIBOR correlations, we yield a semi-parametric framework of non-degenerate correlation structures from which we derive systematically low parametric structures with, in principle, any desired number of parameters [14, 22, 23]. See (1) for an example correlation structure with three parameters $\eta_1, \eta_2, \rho_{\infty}$,where m is the number of LIBORs involved.

 
$\displaystyle\rho_{ij}$ = $\displaystyle\exp\left[-\frac{\vert j-i\vert}{m-1} \left(-\ln\rho_{\infty} +\eta_1\frac{i^2+j^2+ij-3mi-3mj+3i+3j+2m^2-m-4}{(m-2)(m-3)} \right.\right.$   
     $\displaystyle\left.\left. -\eta_2\frac{i^2+j^2+ij-mi-mj-3i-3j+3m+2}{(m-2)(m-3)} \right)\right],$ (1)
     $\displaystylei,j=1,\ldots,m,\quad 3\eta_1\geq\eta_2\geq0,\ 0\leq \eta_1+\eta_2\leq-\ln\rho_{\infty}.$   
As a result, such correlation structure combined with a suitable parametrization of the norm of the deterministic LIBOR/EurIBOR volatility provides a parsimonious multi-factor model with a realistic correlation structure. This allows for stable simultaneous calibration to caps and swaptions via approximative swaption formulas. In the global markets the payment dates of swaps and caps are differently settled. In this respect we improved existing approximation methods for swaptions by taking this issue into account. Further we proposed the incorporation of a stabilizing penalty factor in the RMS object function which prevents the calibration routine from running into degenerate parameter regions. By this penalty function calibration remains stable even if the market data set under consideration contains some internal misalignments. Within the thus constructed framework we carried out various calibration tests which has led to new insights concerning the relationship between the cap and swap markets. Our results will be presented at Risk Europe 2002.

Within an economical context we study the concept of assets and interest rates in a unified model which is completely specified by the assets alone. This allows endogenous derivations of dynamic relations between assets and interest rates from global structural assumptions (homogeneity and some spherical symmetry) on the market. For instance, if c is the drift and b0 the volatility of the short rate, $\bar{\mu}$ the drift and $\bar{\sigma}$ the volatility of the stock index, and $\rho_{I,r}$ the correlation between short rate and index, we obtained:

 
 \begin{displaymath} \frac{c}{\vert b_0\vert} = \rho_{I,r} \left( \frac{\bar{\mu}-r}{\vert\bar{\sigma}\vert^2}-1 \right) \vert\bar{\sigma}\vert.\end{displaymath} (2)

We analyzed such relations further and studied connections among the numeraire portfolio (which is in fact the inverse of the pricing kernel), observable indices, interest rate dynamics, and risk premia. This research was presented at Risk Europe 2001 ([20]).

Within the framework of a risk management system it is necessary not only to validate financial instruments but also to compute their derivations, the so-called Greeks. Due to symmetry relations in a financial market or homogeneity relations of a financial product we obtained relations between the Greeks of a derivative. These results can be used to avoid usually instable numerical differentiations ([21]).

In [15] we developed a Monte Carlo approach for computing option sensitivities. There we find these quantities by Monte Carlo simulation of a corresponding system of stochastic differential equations using weak solution schemes. It turns out that with one and the same control function a variance reduction can be achieved simultaneously for the claim value as well as for the deltas. Recently, we started to investigate Monte Carlo methods for the determination of exercise boundaries of certain American options. The idea is to extend an exercise boundary known up to a certain maturity time by a Monte Carlo procedure. In this procedure we utilize a more sophisticated algorithm for the simulation of stochastic differential equations in the neighborhood of a boundary ([17]).

References:

  1.  P. ARTZNER, F. DELBAEN, J.M. EBER, D. HEATH, Coherent measures of risk, Math. Finance, 9 (1998), pp. 203-228.
  2.  A. BRACE, D. GATAREK, M. MUSIELA, The market model of interest rate dynamics, Math. Finance, 7 (1997), pp. 127-155.
  3.  P. EMBRECHTS, C. KLÜPPELBERG, T. MIKOSCH, Modelling Extremal Events, Springer, Berlin, 1997.
  4.  P. EMBRECHTS, A. MCNEIL, D. STRAUMANN, Correlation: Pitfalls and alternatives, RISK Magazine, 1999.
  5.  J. FRANKE, W. HÄRDLE, G. STAHL, Measuring Risk in Complex Stochastic Systems, to appear in: Lecture Notes in Statist., Springer, Berlin.
  6.  P. GLASSERMAN, X. ZHAO, Arbitrage-free discretization of lognormal forward Libor and swap rate models, Finance Stoch., 4 (2000), pp 35-68.
  7.  P. GLASSERMAN, P. HEIDELBERGER, P. SHAHABUDDIN, Importance sampling and stratification for Value-at-Risk, Proceedings of the Sixth International Conference on Computational Finance, MIT Press, Cambridge, Mass., 2000.
  8.  W. HÄRDLE, H. HERWARTZ, V. SPOKOINY, Multiple volatility modelling, in preparation.
  9.  F. JAMSHIDIAN, LIBOR and swap market models and measures, Finance Stoch., 1 (1997), pp. 293-330.
  10.  S. JASCHKE, The Cornish-Fisher-expansion in the context of delta-gamma-normal approximations, http://www.jaschke-net.de/papers/CoFi.Pdf , Disc. Paper 54, Humboldt-Universität zu Berlin, Sonderforschungsbereich 373, Berlin, 2001.
  11.  \dito , Quantile-VaR is the wrong measure to quantify market risk for regulatory purposes, http://www.jaschke-net.de/papers/VaR-is-wrong.Pdf , Disc. Paper 55, Humboldt-Universität zu Berlin, Sonderforschungsbereich 373, Berlin, 2001.
  12.  S. JASCHKE, U. KÜCHLER, Coherent risk measures and good-deal bounds, Finance Stoch., 5 (2001), pp. 181-200.
  13.  S. JASCHKE, Y. YIANG Approximating value at risk in conditional Gaussian models, to appear in: Applied Quantitative Finance, chapter 1, W. Härdle, T. Kleinow, G. Stahl, Eds., http://www.xplore-stat.de/ebooks/ebooks.html .
  14.   O. KURBANMURADOV, K.K. SABELFELD, J. SCHOENMAKERS, Lognormal random field approximations to LIBOR market models, WIAS Preprint no. 481, 1999, to appear in: J. Comput. Finance.
  15.   G.N. MILSTEIN, J. SCHOENMAKERS, Numerical construction of a hedging strategy against the multi-asset European claim, WIAS Preprint no. 507, 1999, to appear in: Stochastics Stochastics Rep.
  16.  G.N. MILSTEIN, J. SCHOENMAKERS, V. SPOKOINY, Transition density estimation for stochastic differential equations via forward-reverse representations, WIAS Preprint no. 680, 2001.
  17.  G.N. MILSTEIN, M.V. TRETYAKOV, Simulation of a space-time bounded diffusion, Ann. Appl. Probab., 9 (1999), pp. 732-779.
  18.  K.R. MILTERSEN, K. SANDMANN, D. SONDERMANN, Closed-form solutions for term structure derivatives with lognormal interest rates, J. Finance, 52 (1997), pp. 409-430.
  19.  R.B. NELSON, An Introduction to Copulas, Springer, New York, 1999.
  20.  O. REISS, J. SCHOENMAKERS, M. SCHWEIZER, Endogenous interest rate dynamics in asset markets, WIAS Preprint no. 652, 2001.
  21.  O. REISS, U. WYSTUP, Computing option price sensitivities using homogeneity and other tricks, J. Derivatives, 9 (2001), pp. 41-53.
  22.  J. SCHOENMAKERS, B. COFFEY, LIBOR rate models, related derivatives and model calibration, WIAS Preprint no. 480, 1999.
  23.  \dito , Stable implied calibration of a multi-factor LIBOR model via a semi-parametric correlation structure, WIAS Preprint no. 611, 2000.


 [Next]:  Numerical analysis of complex stochastic models  
 [Up]:  Project descriptions  
 [Previous]:  Inference for complex statistical models  
 [Contents]   [Index] 

LaTeX typesetting by I. Bremer
9/9/2002