[Next]:

Applied mathematical finance

[Up]:

Project descriptions

[Previous]:

Project descriptions

 [Contents] 

 [Index] 

Inference for complex statistical models

 

Collaborator: S. Jaschke , P. Mathé , G.N. Milstein , H.-J. Mucha , J. Polzehl , J. Schoenmakers , V. Spokoiny  

Cooperation with: K. Hahn (GSF-IBB, München), F. Godtliebsen (University of Tromsø, Norway), F. Baumgart (Leibniz-Institut für Neurobiologie, Magdeburg), P. Qiu (University of Minnesota, USA), A. Juditski (INRIA, Grenoble, France), M. Hristache (Université de Rennes, France), W. Härdle (SFB 373, Humboldt-Universität zu Berlin), L. Dümbgen (Medizinische Universität Lübeck), J. Horowitz (University of Iowa, USA), S. Sperlich (University Carlos III, Madrid, Spain), D. Mercurio (Humboldt-Universität zu Berlin), B. Grund (University of Minnesota, USA), O. Bunke, B. Droge, H. Herwartz (SFB 373, Humboldt-Universität zu Berlin), A.W. Heemink (Technische Universiteit Delft, The Netherlands), E. Heimerl (Universität Salzburg, Austria), O. Lepski, J. Golubev (Université de Marseille, France), A. Samarov (Massachusetts Institute of Technology, Cambridge, USA), S.V. Pereverzev (Academy of Sciences of Ukraine, Kiev), R. von Sachs (Université Louvain-la-Neuve, Belgium), S. Zwanzig (Uppsala University, Sweden)

Supported by: DFG: SFB 373 ``Quantifikation und Simulation Ökonomischer Prozesse'' (Quantification and simulation of economic processes), Humboldt-Universität zu Berlin; DFG: Priority Program 1114 ``Mathematische Methoden der Zeitreihenanalyse und digitalen Bildverarbeitung'' (Mathematical methods for time series analysis and digital image processing)

Description: Many interesting applications of statistics in economics, finance, and life sciences are based on large databases and complex, high-dimensional models. In these cases, the first goals of statistical analysis are exploratory data analysis, qualitative description of properties of the data, and dimension reduction for further analysis.

Statistical inference includes various methods in statistical modeling, goodness-of-fit tests, and tests of significance for properties identified in the exploratory data analysis.

1. Adaptive techniques for image processing   (J. Polzehl, V. Spokoiny).

Large amounts of two- or three-dimensional images are generated in many fields including medicine, environmental control, meteorology, geology, and engineering. Often decisions have to be based on certain features in the image. To do this the quality of noisy images has to be improved and the features have to be identified. Examples are satellite images, tomographic images, magnetic resonance images (MRI), and ultrasonic images.

Within the project we have developed two new adaptive smoothing   techniques, pointwise adaptation   and adaptive weights smoothing . The first method, described in [32], allows to estimate grey-scale images that are composed of large homogeneous regions with smooth edges and observed with noise on a gridded design. The procedure searches, in each point, for the largest vicinity of the point for which a hypothesis of homogeneity is not rejected. Theoretical properties of the procedure are studied for the case of piecewise constant images. We present a nonasymptotic bound for the accuracy of estimation at a specific grid point as a function of the number of pixel, of the distance from the point of estimation to the closest boundary, and of smoothness properties and orientation of this boundary. It is shown that the proposed method provides a near optimal rate of estimation near edges and inside homogeneous regions.

The second method, Adaptive Weights Smoothing  (AWS) (see [33]), is based on the idea of structural adaptation . The method employs the structural assumption of a specified local model within an iterative procedure. The resulting method has many desirable properties like preservation of edges and contrast, and (in some sense) optimal reduction of noise. The method considerably improves on classical smoothing procedures as soon as the local model provides a reasonable approximation to the image.

Fig. 1 illustrates the reconstruction of a local constant image from a noisy version.

 

Fig. 1: Original (left), image with additive noise (central) and AWS reconstruction from the noisy image (right)  

The idea underlying AWS can be applied to many other types of data. We shortly present an application to classification in dynamic MRI, see [34]. The data, illustrated in Fig. 2, consist of 30 MR images showing, in each voxel, the effect of a contrast agent over time.

 

Fig. 2: Dynamic MRI: 10^th MR Image (left) and typical time series of gray values (right)  

The different behavior in pathologic areas provides the necessary contrast for tissue classification. In this context a vectorized version of AWS can be used to improve tissue classification by adaptive spatial smoothing. Fig. 3 shows the results without (raw data) and with (AWS) spatial adaptive smoothing   for two classification criteria.

 

Fig. 3: Tissue classification from dMRI data 

Currently several generalizations of the structural approach are under development. This especially includes local polynomial adaptive smoothing, varying coefficient models  and likelihood-based methods, e.g., for binary response models.

Research in this field is supported by the DFG Priority Program 1114.

2. Effective dimension reduction (J. Polzehl, V. Spokoiny).  

In many statistical problems one is confronted with high-dimensional data. Typical examples are given by econometric or financial data. For instance, usual financial practice leads to monitoring about 1000 to 5000 different data processes. Single- and multi-index models are often used in multivariate analysis to avoid the so-called ``curse of dimensionality''  problem (high-dimensional data are very sparse). Such models generalize classic linear models and they can be viewed as a reasonable compromise between too restrictive linear and too vague pure nonparametric modeling. For the corresponding analysis, the targets are typically index vectors which allow to reduce the dimensionality of the data without essential loss of information. The existing methods of index estimation can be classified as direct and indirect. The indirect methods like the nonparametric least-squares estimator, or nonparametric maximum-likelihood estimator have been shown to be asymptotically efficient, but their practical applications are very restricted. The reason is that calculation of these estimators leads to an optimization problem in a high-dimensional space, see [17]. In contrast, direct methods like the average derivative estimator, or sliced inverse regression are computationally straightforward, but the corresponding results are far from being optimal, again due to the ``curse of dimensionality'' problem. Their theory applies only under very restrictive model assumptions, see [36], [35] and [4].

Another direct method of index estimation for a single-index model  is proposed in [14]. This method can be regarded as a recursive improvement of the average derivative estimator. The results show that after a logarithmic number of iterations, the corresponding estimator becomes root-n consistent. The procedure is fully adaptive with respect to the design and to unknown smoothness properties of the link function, and results are valid under very mild model assumptions.

For the multi-index situation, [15] proposed a new method of dimension reduction which extends the procedure from [14] and is based on the idea of structural adaptation. The method applies for a very broad class of regression models under mild assumptions on the underlying regression function and the regression design. The procedure is fully adaptive and does not require any prior information. The results claim that the proposed procedure delivers the optimal rate $\, n^{-1/2} \,$ of estimating the index space provided that the effective dimensionality of the model is not larger than 3. The simulation results demonstrate an excellent performance of the procedure for all considered situations. An important feature of the method is that it is very stable with respect to high dimensionality and for a non-regular design.

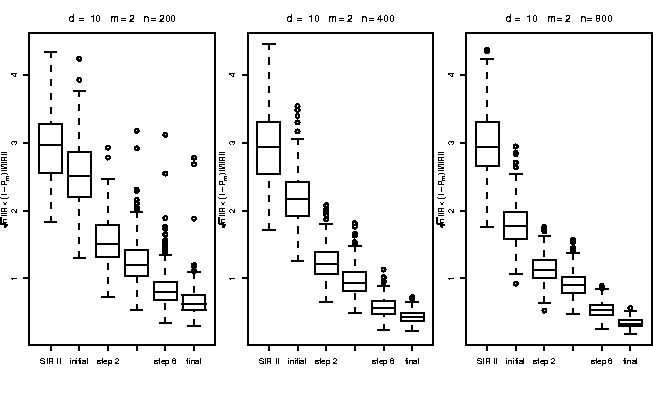
Fig. 4 illustrates the results of a simulation study using a bi-index model $\,Y_i=f(\,X_{i}^T \beta_1, X_{i}^T \beta_2\,) + \varepsilon \,$ with Gaussian errors $\, \varepsilon \,$.The box-plots display the values of a numerical criterion characterizing the quality of the estimated index space for a covariance-based SIR, the ``best'' one-step estimate and after the first, second, fourth, eighth, and final iteration for $\, d=10 \,$, $\, m=2 \,$, and different sample size $\, n \,$. The results displayed are obtained from N=250 simulations.

 

Fig. 4: Simulation results for a bi-index model for m=2, d=10, and n=200, 400, 800. Estimates obtained by SIR II, the initial estimate, 2nd, 4th, 8th, and final iteration.  

3. Statistical inference for time-inhomogeneous finance time series (J. Polzehl, V. Spokoiny).

Log-Returns $\, R_{t}\,$ of the price or currency process in the speculative market are typically modeled using the Conditional Heteroscedasticity   assumption:

$$\begin{eqnarray*} R_{t} = \sigma_{t} \varepsilon_{t},\end{eqnarray*}$$

where $\, \varepsilon_{t} \,$ is a noise process (e.g., white noise) and $\, \sigma_{t} \,$ is a volatility process.   One typical goal of statistical analysis is a few-step-ahead forecasting of the volatility which can be used for portfolio management or Value-at-Risk evaluation. The volatility process is usually modeled using a parametric assumption like ARCH , generalized ARCH (GARCH), stochastic volatility , etc. ([5]). All such models are time homogeneous and therefore fail to capture structural changes of the underlying processes. We developed alternative methods which are based on the assumption of local time homogeneity. More precisely, we assume that the underlying process is time homogeneous within some unknown time interval and the idea of the method is to describe this interval, in a data-driven way. Afterwards one can estimate the current volatility value or one-step volatility forecast simply by averaging over the interval of homogeneity, see [8], [25].

The paper [7] offers an extension of the proposed method to multiple volatility modeling for high-dimensional financial data. The approach involves data transformation, dimension reduction , and adaptive nonparametric smoothing as building blocks.

Fig. 5 demonstrates the results of an adaptive weights smoothing   procedure for time series using the structural assumption of a local ARCH(20) model for the logarithmic returns of the US $ / DM exchange rates in the period 1988-2000. The bottom plot illustrates the segmentation into homogeneous time intervals obtained by the procedure.

 

Fig. 5: Logarithmic returns of US $ / DM exchange rates in the period 1988-2000 (top), estimated volatility within a local ARCH(20) model (center), and first principal component of local parameter estimates 

4. Robust nonparametric hypothesis testing (J. Polzehl, V. Spokoiny).  

Linear quantile regression models are often used in applications. See [2], [18], [20], among others. In contrast to mean regression models, quantile regression   models do not require the individual errors to have moments, are robust to outlying values of the observations, and permit exploration of the entire conditional distribution of the dependent variable. However, there has been little research on testing the hypothesis of linearity. To our knowledge, only [38] and [1] have developed tests of parametric quantile regression models against nonparametric alternatives. In contrast, there is a broad range of literature on testing mean regression models against nonparametric alternatives, see [12] and the references therein.

Paper [13] proposed a new test of the hypothesis that a conditional median function is linear against a nonparametric alternative. The test adapts to the unknown smoothness of the alternative model, does not require knowledge of the distribution of the possibly heterogeneous noise components of the model, and is uniformly consistent against alternative models whose distance from the class of linear functions converges to zero at the fastest possible rate. This rate is slower than $\, n^{-1/2} \,$. In addition, the new test is consistent (though not uniformly) against local alternative models whose distance from the class of linear models decreases at a rate that is only slightly slower than $\, n^{-1/2} \,$. The results of Monte Carlo simulations and an empirical application have illustrated the usefulness of the new test.

In the semiparametric additive hazard regression  model of McKeague and Sasieni ([24]) the hazard contributions of some covariates are allowed to change over time while contributions of other covariates are assumed to be constant. In [6] bootstrap-based test procedures for parametric hypotheses in nonparametric additive survival models  are developed, which can be used to identify covariates with constant hazard contributions.

5. Cluster analysis, multivariate graphics, data mining (H.-J. Mucha).   

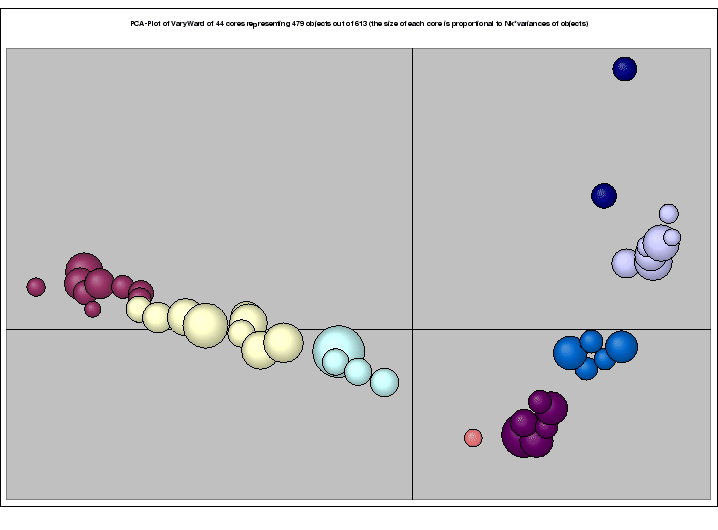
Clustering, in data mining, aims at finding interesting structures or clusters directly from the data without using any background knowledge. The notion of cluster analysis encompasses a great family of methods. Synonyms in use are numerical taxonomy (because of its biological roots), automatic classification, and unsupervised learning. There are model-based as well as heuristic clustering techniques. At most one will set up new hypotheses about the data. At least they aim at a practical useful division of a set of objects into subsets (groups, clusters). This task of subdivision can be attained at the lowest level simply by reordering or sorting techniques. In any case, high-dimensional data visualization (multivariate graphics, projection techniques) and matrix reordering techniques are very useful for visualizing structures and clusters within data ([28]). This indeed is a highly recommended way for a better understanding of both the multivariate high-dimensional data and the results of clustering.

 

Fig. 6: Fingerprint of a distance matrix (data: Roman bricks)

Our statistical software ClusCorr98^®   performs exploratory data analysis mainly by using adaptive methods of cluster analysis, classification, and multivariate graphics. Having data mining applications in mind, some new cluster analysis tools are under development. For example, new model-based clustering techniques using cores are based on weighted observations in order to handle huge data sets effectively ([3]). Intelligent clustering based on dual scaling can handle mixed data. ClusCorr98^® is written in Visual Basic for Applications (VBA) ([29]). It runs under Microsoft Windows taking advantage of the Excel environment including its database facilities.

 

Fig. 7: Principal components plot of eight clusters of cores obtained by modified Ward's method (data: Roman bricks)

6. Numerical analysis of statistical ill-posed problems (P. Mathé).

Ill-posed equations arise frequently in the context of inverse problems, where it is the aim to determine some unknown characteristics of a physical system from data corrupted by measurement errors. Unless special methods, such as Tikhonov regularization, are used, it is often impossible to get sensible results.

In collaboration with S.V. Pereverzev this area of problems is studied for statistical problems

$$y_\delta= A x + \delta\xi,$$

or their discretizations

$$y_{\delta,i}=\langle y_\delta,\varphi_i\rangle = \langle Ax,\varphi_i\rangle + \delta\xi_i,\quad i=1,\dots,n,$$

where A acts injectively and is compact in some Hilbert space, and $\delta\gt$ describes the noise level of the data $y_{\delta,i}$.

Modern numerical analysis has developed a rich apparatus, which reflects different aspects of the sensitivity of ill-posed problems. In Hilbert scales such problems were systematically analyzed since Natterer ([30]). Sometimes, this restriction does not give a flexible approach to estimating realistic convergence rates. Moreover, some important cases are not covered by the ordinary Hilbert scale theory. For these reasons variable Hilbert scales were introduced by Hegland ([9]). Within this framework the solution smoothness is expressed in terms of so-called general source conditions, given by some function over the modulus of the operator A involved in the ill-posed equation. These allow to describe local smoothness properties of the solution. Roughly speaking, in a Hilbert scale with generator L, the norm $\Vert x \Vert _{s}:=\Vert L^{-s}x \Vert _{}$ is replaced by $\Vert x \Vert _{\varphi}:= \Vert \varphi(L^{-1}) x \Vert _{}$, where $\varphi$ is some non-negative function (on the spectrum) of L.

The analysis of ill-posed problems in variable Hilbert scales was further developed in [10] and [37]. In this project the following problems were analyzed.

• How does a given regularization react to smoothness? What has to be assumed about the source condition in order to automatically make use of the given regularization?

  For certain source conditions (power functions or logarithms), first answers were known, see [19], [11], and [31]. In [23] the role of certain geometric properties of the source condition, in particular their concavity, was analyzed.

• A further aspect concerns discretization. Most previous studies were based on spectral theoretical analysis. This restricts consideration to discretizations along the spectrum, which is not realistic. In [21] the authors have indicated how methods from approximation theory allow a more general analysis. This could now be generalized to the context of variable Hilbert scales in [22].

This research constitutes the basis for further investigations of numerical problems in variable Hilbert scales. It shall be continued, supported by the DFG.

7. Statistic and Monte Carlo methods for estimating transition densities for stochastic differential equations (SDEs) (G. Milstein, J. Schoenmakers, V. Spokoiny).

In many applications, for instance in financial and environmental modeling, it is useful to have an efficient algorithm to determine the transition density of a, for example, financial or environmental process given by a stochastic differential equation,

$$dX=a(s,X)ds+\sigma (s,X)dW(s),\;t_{0}\leq s\leq T,$$

where X and a are d-dimensional vectors, W is an m-dimensional standard Wiener process, $\sigma$ is a $d\times m$-matrix, $m\geq d.$

In a cooperation project with ``Applied mathematical finance'' and ``Numerical methods for stochastic models'' we constructed a Monte Carlo estimator for the unknown transition density p(t,x,T,y) for fixed t,x,T,y, which improves upon classical kernel or projection estimators based on approximate realizations of X_t,x(T) directly. For example, the kernel (Parzen-Rosenblatt) density estimator with a kernel K and a bandwidth $\delta$ is given by

$$\hat{p}(t,x,T,y)=\frac{1}{N\delta ^{d}}\sum_{n=1}^{N}K\left( \frac{X_{n}-y}{\delta }\right) ,$$

where $X_{n},\;n=1,...,N,$ are independent approximate realizations of X_t,x(T). It is well-known that even an optimal choice of the bandwidth $\delta$ leads to an error of order N^-2/(4+d). For d>2, this would require a huge sample size N for providing a reasonable accuracy of estimation. In the statistical literature this problem is referred to as ``curse of dimensionality''. Classical Monte Carlo methods allow for an effective estimation of functionals $I(f)=\int p(t,x,T,y)f(y)dy=Ef(X_{t,x}(T))$ by forward diffusion. We derive general reverse diffusion equations for Monte Carlo estimation of functionals $I^{\ast }(g)=\int g(x)p(t,x,T,y)dx.$ The obtained probabilistic representations and the numerical integration of stochastic differential equations (SDEs) together with ideas of mathematical statistics are used for a density estimation by forward-reverse diffusion (see [27]). It is shown that density estimation based on forward-reverse representations allows for essentially better results in comparison with usual kernel or projection estimation based on forward representations only (root-N accuracy instead of N^-2/(4+d)). The following table gives comparative results of a forward-reverse estimator (FRE) with a forward estimator (FE) for an Ornstein-Uhlenbeck-type process (d=1).

 

Table 1: true p=0.518831

$$2\sigma_{FRE} \sigma^2_{FRE}N 2\sigma_{FE} \sigma^2_{FE}N^{4/5}$$ N FRE (sec.) FE (sec.)

10⁴ 0.522 0.031 2.40 2 0.524 0.036 0.51 2

10⁵ 0.519 0.010 2.50 20 0.515 0.016 0.64 18

10⁶ 0.5194 0.0031 2.45 203 0.5164 0.0064 0.65 183

10⁷ 0.5193 0.0010 2.50 2085 0.5171 0.0026 0.68 1854

The developed methods have recently been presented in the Netherlands (Universities of Delft and Amsterdam). These presentations have led to a new scientific cooperation with the group ``Large Scale Systems'' of the Delft University.

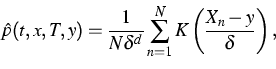
Further, in [16] we proposed asymptotically efficient procedures for estimating the linearized drift of SDEs. Some extremal problems related to nonparametric maximum likelihood estimation of a signal in white noise are investigated in [26].

References:

1.  H.J. BIERENS, D.K. GINTHER, Integrated conditional moment testing of quantile regression models, working paper, Department of Economics, Pennsylvania State University, 2000.
2.  M. BUCHINSKY, Changes in the U.S. wage structure 1963-1987: Application of Quantile Regression, Econometrica, 62 (1994), pp. 405-458.
3.  J. DOLATA, H.-J. MUCHA, H.-G. BARTEL, Archäologische und mathematisch-statistische Neuordnung der Orte römischer Baukeramikherstellung im nördlichen Obergermanien, to appear in: Xantener Berichte 10.
4.  N. DUAN, K.-C. LI, Slicing regression: A link-free regression method, Ann. Statist., 19 (1991), pp. 505-530.
5.  C. GOURIEROUX, ARCH Models and Financial Applications, Springer, 1997.
6.   B. GRUND, J. POLZEHL, Semiparametric lack-of-fit test in an additive hazard regression model, Statistics and Computation, 11 (2001), 311-324.
7.  W. HÄRDLE, H. HERWATZ, V. SPOKOINY, Time inhomogeneous multiple volatility modelling, submitted.
8.  W. HÄRDLE, V. SPOKOINY, G. TESSIÈRE, Adaptive estimation for a time inhomogeneous stochastic-volatility model, submitted.
9.   M. HEGLAND, An optimal order regularization method which does not use additional smoothness assumptions, SIAM J. Numer. Anal., 29 (1992), pp. 1446-1461.
10.  , Variable Hilbert scales and their interpolation inequalities with applications to Tikhonov regularization, Appl. Anal., 59 (1995), pp. 207-223.
11.  T. HOHAGE, Regularization of exponentially ill-posed problems, Numer. Funct. Anal. Optim., 21 (2000), pp. 439-464.
12.  J.L. HOROWITZ, V. SPOKOINY, An adaptive, rate-optimal test of a parametric mean regression model against a nonparametric alternative, Econometrica, 69 (2001), pp. 599-631.
13.  , An adaptive rate-optimal test of linearity for median regression model, WIAS Preprint no. 617, 2000.
14.  M. HRISTACHE, A. JUDITSKY, V. SPOKOINY, Direct estimation of the index coefficients in a single-index model, Ann. Statist., 29 (2001), pp. 595-623.
15.  M. HRISTACHE, A. JUDITSKY, J. POLZEHL, V. SPOKOINY, Structure adaptive approach for dimension reduction, Ann. Statist., 29 (2001), pp. 1537-1566.
16.   R. KHASMINSKII, G.N. MILSTEIN, On estimation of the linearized drift for nonlinear stochastic differential equations, Stoch. Dyn., 1 (2001), pp. 23-43.
17.  R.L. KLEIN, R.H. SPADY, An efficient semiparametric estimator for binary response models, Econometrica, 61 (1993), pp. 387-421.
18.  R. KOENKER, O. GELING, Reappraising medfly longevity: A quantile regression survival analysis, working paper, Department of Economics, University of Illinois, 1999.
19.  O.V. LEPSKII, A problem of adaptive estimation in Gaussian white noise, Teor. Veroyatnost. i Primenen., 35 (1990), pp. 459-470.
20.  W.G. MANNING, L. BLUMBER, L.H. MOULTON, The demand for alcohol: The differential response to price, Journal of Health Economics, 14 (1995), pp. 123-148.
21.   P. MATHÉ, S.V. PEREVERZEV, Optimal discretization of inverse problems in Hilbert scales. Regularization and self-regularization of projection methods, SIAM J. Numer. Anal., 38 (2001), pp. 1999-2021.
22.  , A norm inequality for operator monotone functions, manuscript, 2001.
23.  , Optimality of Tikhonov regularization in variable Hilbert scales, manuscript, 2001.
24.  I.W. MCKEAGUE, P.D. SASENI, A partly parametric additive risk model, Biometrika, 81 (1994), pp. 501-514.
25.  D. MERCURIO, V. SPOKOINY, Statistical inference for time-inhomogeneous volatility models, submitted.
26.  G.N. MILSTEIN, M. NUSSBAUM, Maximum likelihood estimation of a nonparametric signal in white noise by optimal control, Statist. Probab. Lett., 55 (2001), pp. 193-203.
27.   G.N. MILSTEIN, J.G.M. SCHOENMAKERS, V. SPOKOINY, Transition density estimation for stochastic differential equations via forward-reverse representations, WIAS Preprint no. 680, 2001.
28.  H.-J. MUCHA, Clusteranalyse mit Mikrocomputern, Akademie Verlag, Berlin, 1992.
29.  , An intelligent clustering technique based on dual scaling, to appear in: Proc. ICMMA, Banff, Canada.
30.  F. NATTERER, Error bounds for Tikhonov regularization in Hilbert scales, Appl. Anal., 18 (1984), pp. 29-37.
31.  S. PEREVERZEV, E. SCHOCK, Morozov's discrepancy principle for Tikhonov regularization of severely ill-posed problems in finite-dimensional subspaces, Numer. Funct. Anal. Optim., 21 (2000), pp. 901-916.
32.  J. POLZEHL, V. SPOKOINY, Image denoising: Pointwise adaptive approach, to appear in: Ann. Statist.
33.  , Adaptive Weights Smoothing with applications to image restoration, J. Roy. Statist. Soc. Ser. B, 62 (2000), pp. 335-354.
34.  , Functional and dynamic Magnetic Resonance Imaging using vector adaptive weights smoothing, J. Roy. Statist. Soc. Ser. C, 50 (2001), pp. 485-501.
35.  L.J. POWELL, J.M. STOCK, T.M. STOKER, Semiparametric estimation of index coefficients, Econometrica, 57 (1989), pp. 1403-1430.
36.  T.M. STOKER, Consistent estimation of scaled coefficients, Econometrica, 54 (1986), pp. 1461-1481.
37.  U. TAUTENHAHN, Optimality for ill-posed problems under general source conditions, Numer. Funct. Anal. Optim., 19 (1998), pp. 377-398.
38.  J.X. ZHENG, A consistent nonparametric test of parametric regression models under conditional quantile restrictions, Econometric Theory, 14 (1998), pp. 123-138.

[Next]:

Applied mathematical finance

[Up]:

Project descriptions

[Previous]:

Project descriptions

 [Contents] 

 [Index]