Stochastic particle systems as numerical tools

[Next]:

Efficient control of stochastic particle methods

[Up]:

Project descriptions

[Previous]:

Infinite systems of interactive diffusions and

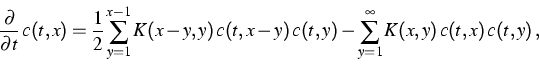
[Contents]

[Index]

Stochastic particle systems as numerical tools for problems in aerosol dynamics

Collaborator: W. Wagner , A. Eibeck

Cooperation with: H. Babovsky (Technische Universität Ilmenau), M. Kraft (University of Cambridge, UK), A. Lushnikov (Karpov Institute of Physical Chemistry, Moscow, Russia), J. Norris (University of Cambridge, UK), K. Sabelfeld (FG 6)

Supported by: DFG Priority Program ``Interagierende Stochastische Systeme von hoher Komplexität'' (Interacting stochastic systems of high complexity), EU, DAAD

Description: The phenomenon of coagulation occurs in a wide range of applications, e.g., in physics (aggregation of colloidal particles, growth of gas bubbles), meteorology (merging of drops in atmospheric clouds, aerosol transport), chemistry (reacting polymers, soot formation), and astrophysics (formation of stars and planets). The time evolution of the average concentration of particles of a given size in some spatially homogeneous physical system is described by Smoluchowski's coagulation equation

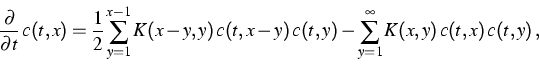$\begin{displaymath} \frac{\partial}{\partial t}\, c(t,x) = \frac{1}{2} \sum_{y=... ...,x-y)\,c(t,y) - \sum_{y=1}^{\infty} K(x,y)\,c(t,x)\, c(t,y)\,, \end{displaymath}$ (1)

where $t\ge 0$ and $x=1,2,\ldots\,.$ The concentration of particles of size x increases as a result of the coagulation of particles of sizes x-y and $y\,.$ It decreases if particles of size x merge with any other particles. The intensity of the process is governed by the (non-negative and symmetric) coagulation kernel K representing properties of the physical medium.

The purpose of the project is to study the relationship between stochastic interacting particle systems and solutions of equations of type (1). On the one hand, results on the asymptotic behavior of the particle system (when the number of particles increases) provide an insight into properties of the solution. On the other hand, appropriate stochastic particle systems are used for the numerical treatment of the macroscopic equation. A basic element of the existing convergence proofs is the uniqueness of the solution to the limiting equation. However, this uniqueness has been established only up to the gelation point

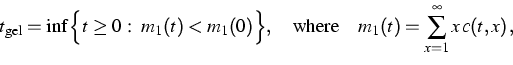$\begin{displaymath} t_{\rm gel}=\inf\Big\{t\ge 0\,:\,\, m_1(t) < m_1(0) \Big\},\quad\mbox{where}\quad m_1(t)=\sum_{x=1}^{\infty} x\,c(t,x)\,,\end{displaymath}$ (2)

which is finite for sufficiently fast increasing coagulation kernels. Thus the problem of convergence after that point is open for general kernels, and numerical observations concerning the behavior of the stochastic processes are of special interest.

At the level of the macroscopic equation (1), the gelation effect is represented by a loss of mass of the solution. An appropriate interpretation of this phenomenon in terms of stochastic particle systems is of both theoretical and practical interest. In the standard direct simulation process gelation corresponds to the formation of a large particle (comparable in size to the size of the whole system) in finite time. An alternative stochastic particle system, called mass flow process, has been introduced in [2]. Its convergence behavior, when the number of particles tends to infinity, was investigated under appropriate assumptions on the coagulation kernel. The derivation is based on some transformation of equation (1) (first used in [1]), and on the approximation of the modified solution. The new algorithm based on the mass flow process has several important features compared to the standard model. First it leads to a considerable variance reduction, when functionals of the solution are calculated. Secondly it shows better approximation properties (faster convergence), especially in the case of gelling kernels. Thus, the mass flow process provides a very efficient tool for studying the gelation effect numerically. Some conjectures based on detailed numerical observations have been stated in [3], [5]. In particular, a new approach to the approximation of the gelation point (2), for a particular class of kernels, has been presented in [5].

An interesting aspect of the mass flow model is the emergence of infinite clusters in finite time for gelling kernels. It has been conjectured in [2] that the (random) explosion times $\tau_{\infty}^n$ of the stochastic system converge (as $n\to\infty$ ) to the gelation time $t_{\rm gel}\,.$ This would connect the gelation effect (a property of the limiting equation) with the explosion phenomenon of a stochastic process, thus representing the physical interpretation of gelation. In this respect we refer to recently announced results ([4]) concerning the explosion behavior of some appropriately scaled tagged particle in the direct simulation process.

The topic of studying coagulation processes by stochastic models has attracted much interest in recent years. Some of the latest results in this field have been reported at a workshop in Oberwolfach last summer (cf. [6]). In particular, a better theoretical understanding of the gelation phenomenon, as well as the study of the spatially inhomogeneous case, are a challenge for future research.

References:

H. BABOVSKY, On a Monte Carlo scheme for Smoluchowski's coagulation equation, Monte Carlo Methods Appl., 5 (1999), pp. 1-18.
A. EIBECK, W. WAGNER, Stochastic particle approximations for Smoluchowski's coagulation equation, Ann. Appl. Probab., 11 (2001), pp. 1137-1165.
$\dito$ ,Stochastic algorithms for studying coagulation dynamics and gelation phenomena, Monte Carlo Methods Appl., 7 (2001), pp. 157-165.
P. MARCH, A tagged particle in coagulation processes, in [6], p. 6.
W. WAGNER, Stochastic, analytic and numerical aspects of coagulation processes, WIAS Preprint no. 697, 2001.
Stochastic models for coagulation processes, Mathematisches Forschungsinstitut Oberwolfach, Report 39/2001. See T0134c">http://www.mfo.de/Meetings/ $\char93$ T0134c .