Infinite systems of interactive diffusions and

[Next]:

Stochastic particle systems as numerical tools

[Up]:

Project descriptions

[Previous]:

Phase transitions and statistical mechanics

[Contents]

[Index]

Infinite systems of interactive diffusions and their equilibrium states

Collaborator: S. R $\oe$ lly

Cooperation with: P. Dai Pra (Università degli Studi di Padova, Italy), D. Dereudre (École Polytechnique, Palaiseau, France), M. Thieullen (Université Paris VI, France), H. Zessin (Universität Bielefeld)

Description: The concept of reciprocal processes can be traced back to E. Schrödinger. They form a class of stochastic processes that generalize the notion of Markov processes and are defined via a temporal Markovian field property. They play an important role in the context of Quantum Diffusions, Nelson's stochastic mechanics, and several variational problems such as entropy maximization on path space.

In a collaboration with M. Thieullen ([1]) we characterize real-valued reciprocal processes associated to a Brownian diffusion as a solution of an integration-by-parts formula. In this characterization appears a function, called reciprocal characteristics, that turns out to play the same role as the Hamiltonian in statistical mechanics. This approach is systematically applied in the context of periodic Ornstein-Uhlenbeck processes. The same approach was also carried through in the multi-dimensional setting. The next major goal of this project is an extension to infinite-dimensional situations, where the reciprocal process is the solution of a stochastic partial differential equation.

In collaboration with P. Dai Pra and H. Zessin, we have developed a characterization of the stationary law of interacting diffusion processes indexed by the lattice ${\Bbb Z}^d$ as Gibbsian measures. Let $X=\{X_i(t), i \in {\mathbb Z}^d, t \in {\mathbb R}\}$ be the weak solution of the Stochastic Differential Equation

$\begin{displaymath} (*) \hspace{1cm} dX_i(t) = \Big(- \frac{1}{2}\varphi'(X_i(t)... ...Big)dt + dB_i(t) \ , i \in {\mathbb Z}^d, t \in {\mathbb R}\,, \end{displaymath}$

where ${\bf b}_{i,t}$ is a measurable bounded local functional on the path space, a priori non Markovian. Then the law Q of X can be interpreted as Gibbs distribution on $\Omega = {\cal{C}}({\mathbb R},{\mathbb R})^{{\mathbb Z}^d}$ , with a priori measure P the product of Wiener measures drifted by $-\frac{1}{2}\varphi'$ and a certain interaction potential $\Phi$ . The main result in [2] shows the following equivalence

Q is a stationary solution of the SDE (*).
Q is a space-time shift invariant Gibbs state.
Q minimizes the free energy ${\cal{H}}^{\bf b}(Q')= {\cal{H}}(Q') -E_{Q'}(\Phi)$ , where ${\cal{H}}(Q')$ denotes the specific entropy of Q' with respect to P.

The technique is based on Girsanov transformation, stochastic analysis, and the classical variational principle of Statistical Mechanics.

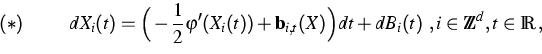
In [3], the above results are completed by an existence result for the solution of (*). The authors use a space-time cluster expansions method, well adapted when the coupling parameter ${\bf b}$ is sufficiently small.

References:

S. R $\oe$ lly, M. THIEULLEN, A characterization of reciprocal processes via an integration by parts formula on the path space, to appear in: Probab. Theory Related Fields (2002).
P. DAI PRA, S. R $\oe$ lly, H. ZESSIN, A Gibbs variational principle in space-time for infinite dimensional diffusions, Probab. Theory Related Fields, 122 (2002), pp. 289-315.
P. DAI PRA, S. R $\oe$ lly, An existence result for infinite-dimensional Brownian diffusions with non-regular and non-Markovian drift, in preparation.