Mehrskalensysteme

[Next]:

Forschungsgruppe Numerische Mathematik und Wissenschaftliches Rechnen

[Up]:

Projektbeschreibungen

[Previous]:

Normalformen für homokline Bifurkationen

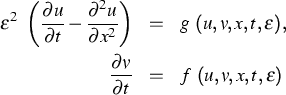
[Contents]

[Index]

Mehrskalensysteme

Bearbeiter: K. R. Schneider

Teilprojekt 1: Stabilitätswechsel in Mehrskalensystemen

Kooperation: V. F. Butuzov, N. N. Nefedov (Staatliche Universität Moskau, Russland)

Förderung: DFG: Kooperationsprojekt ,,Singulär gestörte Systeme und Stabilitätswechsel`` deutscher und russischer Wissenschaftler im Rahmen des Memorandum of Understanding zwischen DFG und RFFI

Beschreibung der Forschungsarbeit:

Im Rahmen der Forschungskooperation zwischen dem Weierstraß-Institut und dem Fachbereich Mathematik der Physikalischen Fakultät der Staatlichen Universität Moskau auf dem Gebiet des Stabilitätswechsels bei Mehrskalensystemen und dessen Anwendung auf reaktionskinetische Prozesse wurde im Berichtszeitraum der Schritt in Richtung parabolischer Gleichungen vollzogen (in den vorangegangenen Jahren ging es um gewöhnliche Differentialgleichungen und um elliptische Probleme). Es wurden singulär gestörte teilweise dissipative Reaktions-Diffusionsgleichungen der Gestalt

$\parbox {13cm}{ \begin{eqnarray*} \varepsilon^2 \ \left(\frac{\partial u}{\parti... ...\ \frac{\partial v}{\partial t} & = & f \ (u,v,x,t,\varepsilon)\end{eqnarray*}}$ $% latex2html id marker 2515 \parbox {1cm}{\begin{eqnarray}\end{eqnarray}}$

betrachtet, wobei u und v skalare Funktionen sind und $\varepsilon$ ein kleiner positiver Parameter ist. Gleichungen dieser Gestalt spielen bei der Modellierung von Prozessen eine Rolle, wenn der Effekt der Diffusion auf eine der Substanzen vernachlässigbar ist. Falls die ausgeartete Gleichung

$\begin{eqnarray} g \ (u,v,x,t,0) & = & 0\end{eqnarray}$

eine bezüglich u isolierte Lösung besitzt, kann die Standardtheorie [1] angewandt werden, um asymptotische Eigenschaften der Lösung von Anfangsrandwertproblemen abzuleiten.

Die gemeinsamen Untersuchungen bezogen sich auf den Fall, dass die ausgeartete Gleichung zwei Lösungen $u=\varphi_1 (v,x,t)$ und $u=\varphi_2 (v,x,t)$ besitzt, die sich transversal in einer Fläche schneiden, deren Projektion in den (v,x,t)-Raum durch v=s(x,t) beschrieben wird. Diese Annahme hat einen Stabilitätswechsel der Familien von Gleichgewichtspunkten der assoziierten Differentialgleichung

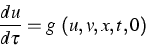
$\begin{displaymath} \frac{du}{d\tau} = g \ (u,v,x,t,0)\end{displaymath}$

zur Folge. Das Hauptresultat der Untersuchungen [2] besteht im Beweis eines Satzes über die Existenz einer eindeutigen Lösung des Anfangsrandwertproblems

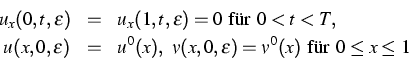
$\begin{eqnarray*} u_x (0,t,\varepsilon) & = & u_x (1,t,\varepsilon) =0 \mbox{ fü... ...^0 (x), \ v(x,0,\varepsilon) = v^0 (x) \mbox{ für } 0 \le x \le 1\end{eqnarray*}$

für (1) und ihres asymptotischen Verhaltens in $\varepsilon$ für $\varepsilon \rightarrow 0$ . Die Beweise basieren auf der Methode der asymptotischen Unter- und Oberlösungen. Die erhaltenen Ergebnisse (Änderung des asymptotischen Verhaltens aufgrund der Änderung des Stabilitätsverhaltens) können verwendet werden, um das Sprungverhalten der Reaktionsrate in derartigen Systemen zu erklären.

Die erhaltenen Ergebnisse können auf Systeme übertragen werden ([3]).

Projektliteratur:

A. B. VASIL'EVA, V. F. BUTUZOV, L. V. KALACEV, The boundary function method for singular perturbation problems, SIAM, Philadelphia, 1995.
V. F. BUTUZOV, N. N. NEFEDOV, K. R. SCHNEIDER, Singularly perturbed partly dissipative reaction-diffusion systems in case of exchange of stabilities , WIAS-Preprint No. 572 , 2000.
$\dito$ ,On a class of singularly perturbed partly dissipative reaction-diffusion systems, in Vorbereitung.

Teilprojekt 2: Stabilisierung singulär gestörter Kontrollsysteme

Kooperation: V. V. Strygin (Staatliche Universität Voronesh, Russland), E. Fridman (Universität Tel Aviv, Israel)

Förderung: Minerva-Stiftung

Beschreibung der Forschungsarbeit:

Wir betrachten dynamische Systeme mit schnellen und langsamen Zustandsgrößen

$\parbox {13cm}{ \begin{eqnarray*} \frac{dx}{dt} & = & X(x,y,\lambda), \ \varepsilon \ \frac{dy}{dt} & = & Y (x,y,\lambda),\end{eqnarray*}}$ $% latex2html id marker 2523 \parbox {1cm}{\begin{eqnarray}\end{eqnarray}}$

wobei $x \in R^n, \ y \in R^M, \ 0 < \varepsilon \ll 1$ gilt. $\lambda$ ist ein k-dimensionaler Parameter. Wir nehmen an, dass (1) für $\lambda = \lambda_0$ einen instabilen Gleichgewichtspunkt (x₀ ,y₀) besitzt. Das Ziel besteht in der Stabilisierung des Gleichgewichtspunktes durch Applikation einer Vibrationskontrolle. In [1] wird die Vibrationskontrolle durch schnelle (fastperiodische) Variationen des Parameters $\lambda$ realisiert

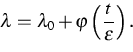$\begin{displaymath} \lambda = \lambda_0 + \varphi \left(\frac{t}{\varepsilon}\right).\end{displaymath}$ (2)

Es werden Bedingungen abgeleitet, unter denen die Lösung des Anfangswertproblems von (1) unter der Voraussetzung (2) als asymptotische Reihe in $\varepsilon$ dargestellt werden kann. Unter Verwendung von Mittelungsmethoden und der Methode der Randschichtfunktionen kann das Restglied abgeschätzt werden.

In [2] wird das Stabilisierungsproblem von einem allgemeineren Standpunkt aus betrachtet (es werden nicht nur Parametervariationen als Steuerungsfunktionen verwendet), und zu seiner Lösung werden mehr geometrische Zugänge verwendet.

Zu diesem Zweck wird das Kontrollsystem

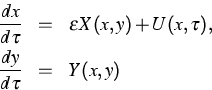
$\begin{eqnarray*} \frac{dx}{d\tau} & = & \varepsilon X(x,y)+ U(x,\tau), \ \frac{dy}{d\tau} & = & Y(x,y)\end{eqnarray*}$

mit $\tau:= t/\varepsilon$ betrachtet. Es soll die Steuerung $U(x,\tau)$ so bestimmt werden, dass der unkontrollierte instabile Zustand (x₀, y₀) stabilisiert wird. Unter Verwendung von Resultaten über die Persistenz normal hyperbolischer invarianter Mannigfaltigkeiten und durch die Anwendung der Mittelungstheorie und weiterer geeigneter Koordinatentransformationen werden hinreichende Bedingungen für die Stabilisierbarkeit abgeleitet. Gleichzeitig werden modifizierte Konzepte der Vibrationsstabilisierung eingeführt und mit den klassischen Definitionen an Beispielen verglichen.