| = | (1) |
|
|
[Contents] | [Index] |
Collaborator: W. Dreyer (FG 7), M. Herrmann (FG 7), A. Möller (FG 7), J. Sprekels
(FG 1)
Cooperation with: M. Kunik (Otto-von-Guericke Universität Magdeburg), A. Mielke (Universität Stuttgart)
Supported by: DFG: Priority Program ``Analysis, Modellbildung und Simulation von Mehrskalenproblemen'' (Analysis, modelling and simulation of multiscale problems)
Description:
In this project we study the initial value problem for an atomic chain
consisting of a large number N of identical atoms. The dynamics of
the chain is governed by Newton's equation
Our main goal is to develop and to apply mathematical methods in order to pass to the macroscopic limit that results if the particle number N tends to infinity.
In the last report period we concentrated on the following setting for micro-macro transitions in the atomic chain.
| (2) |
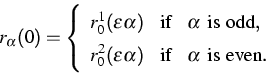 |
(3) |
There are at least two reasons why these initial data are interesting
for micro-macro transitions. Firstly, they pose an effective but
simple possibility to create an initial temperature field in the
chain. Secondly, in the case that r01, r02 and v01,
v02 are constant, we can rigorously pass to the limit
![]() . All interesting thermodynamical quantities are
then determined by a single ODE
. All interesting thermodynamical quantities are
then determined by a single ODE
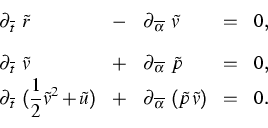 |
(5) |
| (6) |
Furthermore, in [1] and [2] we predict the local distribution functions for the atomic velocities and atomic distancies and we derive the Gibbs equation for (5).
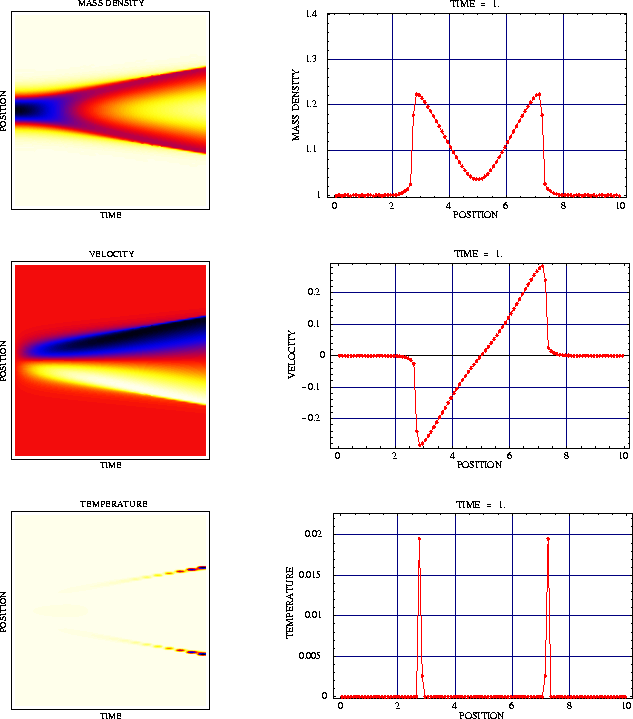
Numerical simulations indicate that the above-mentioned assumption leads to an appropriate description of the atomic chain for very large particle numbers. This fact is illustrated by the following figures.
Figure 1 shows the macroscopic initial configuration of a chain with 16000 atoms. The interaction potential is the well-known Toda potential.
The resulting data for ![]() are depicted in
Figure 2. The highly oscillating functions, which are not observable
on the macroscopic scale correspond to atomic distancies and
velocities. The dark-colored macroscopic curves are the mean values of
the microscopic oscillations and represent the specific length
are depicted in
Figure 2. The highly oscillating functions, which are not observable
on the macroscopic scale correspond to atomic distancies and
velocities. The dark-colored macroscopic curves are the mean values of
the microscopic oscillations and represent the specific length ![]() and the macroscopic velocity
and the macroscopic velocity ![]() .
.
The last figure contains four examples of local distribution functions of the atomic distancies. The light-colored and continuous curves have been calculated by means of the macroscopic fields. The dark-colored and dotted curves correspond to the distribution functions according to Newton's equations.
Regarding the numerical solution of the microscopic equation of motion, the Verlet-Stoermer as well as the velocity-Verlet method are used. Both methods are applicable to molecular dynamics, however, the velocity-Verlet method tends to be more suitable to maintain the symplectic structure [3, 6] of the equation.
There follow two examples illustrating some of the numerical studies.
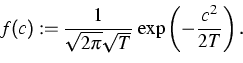
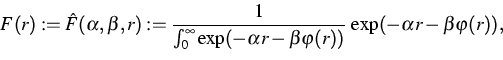
To prepare the atomic chain in thermal equilibrium, in [1]
Section 9.2, the authors start with an equidistant distribution of the
distances ![]() and a distribution of the thermal velocities
according to some auxiliary temperature
and a distribution of the thermal velocities
according to some auxiliary temperature ![]() .
Solving the microscopic equation of motion after some iteration the
distributions f(v) and F(r) will appear approximately.
.
Solving the microscopic equation of motion after some iteration the
distributions f(v) and F(r) will appear approximately.
To overcome the pre-iterations, the distribution of the velocities may
be simulated by a random number generator for the Gaussian distribution
as above using the initial temperature T instead of the auxiliary
temperature ![]() .Since the cumulative distribution function of F is bijective, the
distances may be generated by the inverse transform method
[5].
For this purpose a sequence of random numbers
.Since the cumulative distribution function of F is bijective, the
distances may be generated by the inverse transform method
[5].
For this purpose a sequence of random numbers ![]() will be generated which are uniformly distributed on [0,1].
Next the distances are initialized by ri := G-1(ui) where
G denotes the distribution function of F.
Then the resulting sequence
will be generated which are uniformly distributed on [0,1].
Next the distances are initialized by ri := G-1(ui) where
G denotes the distribution function of F.
Then the resulting sequence ![]() will be distributed
according to the density F.
will be distributed
according to the density F.
References:
|
|
[Contents] | [Index] |