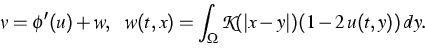[Next]:

Upscaling of microscopically calculated characteristics to

[Up]:

Project descriptions

[Previous]:

Project descriptions

 [Contents] 

 [Index] 

On a nonlocal model of image segmentation

Collaborator: H. Gajewski (FG 1), K. Gärtner

(FG 3) Description: Understanding an image as binary grey ``alloy'' of a black and a white component, we use a nonlocal phase separation model [1], [3], [4] to describe image segmentation and noise reduction.

The model consists in a degenerate nonlinear parabolic equation with a nonlocal drift term additionally to the familiar Perona-Malik model:

$$\frac{\partial u}{\partial t} - \nabla \cdot [f(\vert\nabla ... ...abla w}{\phi ''(u)})] + \beta (u-g)=0, ~~ u(0,\cdot)= g(\cdot),$$

where

$$v = \phi'(u) + w,~~ w(t,x) = \int_\Omega {\cal K}(\vert x-y\vert) (1 - 2\, u(t,y))\, dy.$$

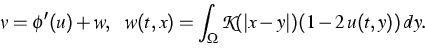
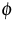$\phi$ is a convex function, the kernel 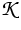${\cal{K}}$ represents nonlocal attracting forces, and v may be interpreted as chemical potential.
u has the meaning of a concentration/modified image, and g is the initial value/noisy image, respectively.
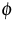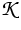Relevant examples for $\phi$ and ${\cal{K}}$ are given by $\phi(u)=u \log u + (1-u) \log (1-u),\;\; 0\le u \le 1$, ${\cal K}(s)= k e^{-s/\sigma}$.
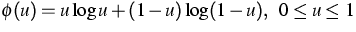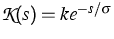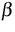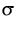The model parameters ($\beta$, k, $\sigma$ in the example) can be adjusted by minimizing a functional evaluating smoothness and entropy of u and the distance between u and g.

We formulate conditions for the model parameters to guarantee global existence of a unique solution that tends exponentially in time to a unique steady state. This steady state is solution of a nonlocal nonlinear elliptic boundary value problem and allows a variational characterization.

The application of the model to noise reduction is related to model parameters guaranteeing a unique steady state. Image segmentation is related to parameters where a unique steady state may not exist.

Figure 1 demonstrates some properties of the model applied to the noise reduction problem.

References:

1. H. GAJEWSKI, On a nonlocal model of non-isothermal phase separation, WIAS Preprint no. 671 , 2001, to appear in: Adv. Math. Sci. Appl.
2. H. GAJEWSKI, K. GÄRTNER, On a nonlocal model of image segmentation, WIAS Preprint no. 762 , 2002.
3. H. GAJEWSKI, K. ZACHARIAS, On a nonlocal phase separation model, WIAS Preprint no. 656 , 2001, to appear in: J. Math. Anal. Appl.
4. G. GIACOMIN, J.L. LEBOWITZ, Phase segregation dynamics in particle systems with long range interactions I. Macroscopic limits, J. Statist. Phys., 87 (1997), pp. 37-61.

Fig. 1: Noisy picture (157 by 124 pixel section, UL), first optimization step (UR),

[Next]:

Upscaling of microscopically calculated characteristics to

[Up]:

Project descriptions

[Previous]:

Project descriptions

 [Contents] 

 [Index]