Collaborator: W. Dreyer
,
M. Herrmann
, Sh. Qamar
Cooperation with: M. Kunik (Otto-von-Guericke-Universität
Magdeburg), M. Junk (Universität Kaiserslautern)
Supported by: DFG: ``Kinetische Behandlung von ausgewählten Anfangs- und
Randwertproblemen'' (Kinetic solution of sample initial and
boundary value problems), Priority Program ``Analysis und Numerik
von Erhaltungsgleichungen'' (ANumE -- Analysis
and numerics for conservation laws)
Description:
At low temperatures the evolution of heat in crystalline solids is
carried by phonons. In particular, the
Fourier theory of heat fails to describe heat
conduction at low temperatures. The evolution of a phonon gas is
governed by the Boltzmann-Peierls equation which is a kinetic equation for the phase density 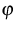 of a phonon gas. For more details we refer to [6] and [4].
The Boltzmann-Peierls equation may be written as
of a phonon gas. For more details we refer to [6] and [4].
The Boltzmann-Peierls equation may be written as
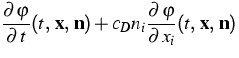 |
= |
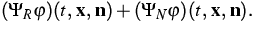 |
(1) |
Here t, 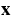 and
and 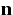 denote the time, the space and
the normal wave vector, respectively. The collision operators
denote the time, the space and
the normal wave vector, respectively. The collision operators 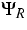 and
and 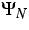 are relaxation operators and model the phonon-phonon
interactions as well as the influence of the lattice.
are relaxation operators and model the phonon-phonon
interactions as well as the influence of the lattice.
The Boltzmann-Peierls equation
implies a hierarchy of balance equations
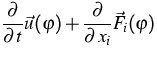 |
= |
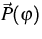 |
(2) |
for densities 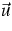 , fluxes
, fluxes 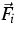 and
productions
and
productions 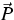 .The extended thermodynamics uses the kinetic entropy h, which here
reads
.The extended thermodynamics uses the kinetic entropy h, which here
reads
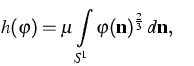 |
|
|
(3) |
and the Maximum Entropy
Principle (MEP) in order to close a finite system of balance
equations. There result symmetric hyperbolic systems of PDEs.
The main problems we investigate in this project may be
summarized as follows
- 1.
- Existence of MEP operators and properties of the corresponding
moment systems;
- 2.
- Kinetic approximations for the MEP moment systems that have the form
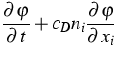 |
= |
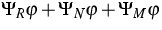 |
(4) |
with a suitable relaxation operator 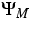 ;
; - 3.
- Kinetic schemes for the kinetic equations as well as for the
moment systems;
- 4.
- Mathematical justification of the thermodynamical strategy to
replace a kinetic equation by a hyperbolic moment system.
In the last year we concentrated on the mathematical properties of the
above-mentioned nonlinear operators and equations. We obtained partial
results concerning
- 1.
- Estimates that control Lp bounds for MEP phase densities;
- 2.
- Local existence and global uniqueness results for
the Boltzmann-Peierls equation and
for the kinetic approximations of MEP moment systems;
- 3.
- Modified collision and MEP operators leading to
global existence results.
References:
- W. DREYER, M. HERRMANN, M. KUNIK, Kinetic
schemes and initial boundary value problems for the Euler system,
Transport Theory Statist. Phys., 31 (2002), pp. 1-33.
-
 , Kinetic
solutions of the Boltzmann-Peierls equation and its moment systems,
, Kinetic
solutions of the Boltzmann-Peierls equation and its moment systems,
WIAS Preprint no. 709, 2001.
- W. DREYER, M. JUNK, M. KUNIK, On the
approximation of kinetic equations by moment systems,
Nonlinearity, 14 (2001), pp. 881-906.
- W. DREYER, M. KUNIK, Initial and boundary
value problems of hyperbolic heat conduction,
Contin. Mech. Thermodyn. 11 (1999), pp. 227-245.
- W. DREYER, M. KUNIK, Kinetische Behandlung von
ausgewählten hyperbolischen Anfangs- und Randwertproblemen,
DFG Proposal DR 401/2-2.
- W. DREYER, H. STRUCHTRUP, Heat pulse
experiments revisited, Contin. Mech. Thermodyn., 5 (1993),
pp. 3-50.
- M. KUNIK, S. QAMAR, G. WARNECKE,
Kinetic schemes for the relativistic gas dynamics, Preprint
no. 40, Otto-von-Guericke University, Magdeburg, 2002.
LaTeX typesetting by I. Bremer
5/16/2003
![]() of a phonon gas. For more details we refer to [6] and [4].
The Boltzmann-Peierls equation may be written as
of a phonon gas. For more details we refer to [6] and [4].
The Boltzmann-Peierls equation may be written as