[Next]:  Research Group Continuum Mechanics  
 [Up]:  Project descriptions  
 [Previous]:  Applied mathematical finance  
 [Contents]   [Index] 

Subsections

Numerical analysis of complex stochastic models

Collaborator: A. Kolodko , D. Kolyukhin , G.N. Milstein , K.K. Sabelfeld

Cooperation with: Ch. Engelhardt (Leibniz-Institut für Gewässerökologie und Binnenfischerei, Berlin) T. Foken (Universität Bayreuth), N.O. Jensen (Risoe National Laboratory, Denmark), V. Kukharets (Obukhov Institute of Atmospheric Physics, Moscow, Russia), O. Kurbanmuradov (Physics and Mathematics Research Center, Turkmenian State University, Ashkhabad) A. Levykin, I. Shalimova (Institute of Computational Mathematics and Mathematical Geophysics, Russian Academy of Sciences, Novosibirsk), M. Mascagni (Florida State University, Tallahassee, USA), O. Smidts (Université Libre de Bruxelles, Belgium), M. Tretiakov (University of Leicester, UK), H. Vereecken (Forschungszentrum (FZ) Jülich, Institut für Chemie und Dynamik der Geosphäre), T. Vesala and Y. Rannik (Helsinki University, Finland)

Supported by: INTAS Grant INTAS-99-1501, NATO Linkage Grant N978912, DFG

Description:

Stochastic models serve as a powerful instrument for studying the dynamics of processes in natural and life sciences, in the broad spectrum, from simple models of financial mathematics in the form of systems of stochastic differential equations we studied in [15] and [19], to very complicated turbulence models involving PDEs. Parameters of such equations are random fields, governing the movement of energy spectrum from smallest viscous scales to large energy-containing vorteces in the boundary layer of atmosphere and rivers we simulated in [3], [11], [16], and [29]. The principal research efforts were directed to the development of new stochastic models and simulation techniques for solving elasticity problems, transport of pollutants, gases and aerosol particles in the turbulent atmosphere, porous media, rivers and soil, as well as for stochastic Hamiltonian systems and Langevin-type equations. As a basis research used in these applied studies, different inner problems of the intrinsic stochastic numerical methods are investigated.

1. Random Walk methods for elasticity problems

(K.K. Sabelfeld).

In many interesting boundary value problems the geometry of the domain is extremely complicated, and this is one of the main motivations for the development of the grid-free methods, e.g., particle and smoothed-particle methods. In stochastic simulation, we deal with two popular techniques of this kind: (1) the Random Walk methods based on the probabilistic representation of the solutions in the form of an expectation over random diffusion processes, and (2) the Probability Density Function (PDF) method which exploits the fact that the joint pdf of the state of the system satisfies some PDEs. However both methods have strong restrictions: The first one is known only for classical scalar PDEs, and becomes unefficient near the boundary because it is forced to make the integration step smaller and smaller. The PDF method is applied to a much broader class of problems, including nonlinear problems for the Navier-Stokes equation, but it cannot be considered as a rigorous method because it describes the processes in the framework of one-particle-fixed time distributions and involves therefore some semi-empirical closure assumptions.

The Random Walk methods which are based on the Monte Carlo solution of the equivalent integral equations present another class of methods which provide rigorous (i.e., with estimation of the accuracy) numerical solution of linear and nonlinear equations [27], [32]. We develop two different classes of Random Walk methods: the Walk on Boundary methods, and the Walk inside the domain. The Random Walk on Boundary methods are in a sense stochastic counterparts of the boundary element methods [33]. The method is grid free and uses random points on the boundary. We are developing such methods for different second-order parabolic and elliptic equations and systems of elliptic equations. What is very important, in this method, in contrast to the conventional probabilistic representations, is that all boundary conditions are possible, and the exterior problems are solved by the same Random Walk on Boundary process. In the class of Random Walk inside the domain, we develop new versions of the Walk on Spheres method which enables us to solve systems of elliptic equations, for instance, the Lamé equation governing the static elasticity processes. In some sense this is a stochastic version of the Schwarz alternative procedure, but the numerical efficiency is much higher for problems of high dimension. We constructed convergent stochastic algorithms for solving the Lamé equation for a broad class of two- and three-dimensional domains [28] [30], [34], [35].

In a cooperation with the group of Professor M. Mascagni (Florida State University, Tallahassee, USA), the permeability for a complicated geometry of a porous medium is studied to find the distribution of the velocity field. The methods used are the Decentred Random Walk on Spheres (DRWS) suggested by K.K. Sabelfeld and I. Shalimova [35]. In a cooperation with the Institute of Computational Mathematics and Mathematical Geophysics, Russian Academy of Sciences, Novosibirsk, an additional validation of the model based on the DRWS method is made by applying the Random Walk on Boundary process.

2. Footprint problem

(K.K. Sabelfeld).

One field where the stochastic Lagrangian models are very efficiently applied is the footprint problem.

When carrying out micrometeorological measurements of various scalar surface fluxes, for instance, CO2 flux from vegetation, evaporation of fertilizer volatilization, the following problems arise: Since the fluxes are given as a correlation between the velocity and concentration of the constituent considered, the sensor cannot be placed too close to the ground for many reasons, in particular, the wind speed there is very small and the size of the measurement instruments is comparable to the length scale of the small eddies near the ground. In addition, near the surface you are in the roughness layer, where you cannot use the typical atmospheric surface-layer parametrizations.

The higher the measurement point is placed, the weaker is the signal from the ground, since more of the vertical surface flux is converted into a mean horizontal flux by advection. Also as the measurement height is increased, the sensor ``observes'' more of the upwind area. Thus if the sensor is placed above a field which abuts on a forest (in the upwind direction), some part of the measurement flux might stem from the forest and not from the field. The analysis of the elevated measurements is also pertinent to inferring surface fluxes from aircraft measurement. The problem now is twofold: How much weaker is the signal in the measurement height and how does the upwind area contribute to the flux in the measurement point. Footprint analysis made for horizontally homogeneous areas give an estimate of how much homogeneous fetch is needed to make the assumption of horizontal homogeneity valid. The analysis can be used for quantifying the reliability of measurements. One might think also of a footprint analysis before the erection of a mast for several possible positions in order to find ``the best'' positioning for the mast.

We develop stochastic models and codes for the evaluation of concentration and flux footprint functions, see [10], [11], [12], [16], [26]. Parametrization of the surface layer of atmosphere and comparison with the experimental measurements are made in cooperation with Helsinki (Finland), Risoe (Denmark) and Bayreuth (Germany) universities.

3. Turbulence simulation of the river flow

(K.K. Sabelfeld).

Unlike most existing stochastic Lagrangian models, in our model (suggested in [9]) the Eulerian pdf pE may be non-Gaussian, as, for instance, in the forest canopy [5]. It is believed that the model proposed is well suited for the case of a neutrally (or close to neutrally) stratified surface layer, which is one of the interesting tasks. One example is the simulation of the turbulent flow in a river we have carried out in cooperation with the Leibniz Institute of Freshwater Ecology and Inland Fisheries, Berlin, [3].

The effect of turbulence on aquatic photosynthetic organisms transported by river flow is generally associated with two distinctive scales. On a river depth scale (large scale), the turbulence mixing determines the dynamics of light supply to the suspended algae. The algae cells experience a fluctuating intensity and spectral composition of light due to its exponential, wave-length-dependent decline with distance from the free surface of flow. At a given light dosage, the intensity of mixing in the vertical plane influences the rate of photosynthesis, the inhibitory effects of UV and algae growth rate. The algae size varies broadly from the size of an individual cell to the size of large colonies or aggregates. On a scale of aggregates (small scale), the shear stresses control the rate of aggregation for algae colonies and their disruption. The maximum size of aggregates is limited by a characteristic microscale of river turbulence, Kolmogorov's scale, the scale at which hydrodynamic stresses could tear aggregates to pieces. Thus, properties of environment represented by turbulent flow play a critical role in the development of biological processes.

The results of simulation are given in [36].

4. Transport of interacting particles in porous media

(A. Kolodko, D. Kolyukhin, K.K. Sabelfeld).

The study, prediction, and computation of the transport of particles within a porous medium advected by laminar or turbulent flows is a very challenging problem with broad applicability in many environmental and industrial areas [2], [4]. In addition, understanding flows through porous media is crucial to the efficient and environmental recovery of petrochemicals and other mineral resources.

Physically, the problem of flow through porous media includes an enormously wide range of spatial and temporal scales. The extremely high spatial heterogeneity makes conventional deterministic numerical methods practically ineffective. If one considers, for example, only the deterministic computation of even slightly turbulent flow in a porous medium the computational resources required to perform a direct numerical simulation exceed those available on even the most powerful and advanced of today's parallel supercomputers.

Therefore, a probabilistic numerical approach, which requires fewer computational resources, is quite natural as many of the parameters of the porous medium including the permeability, porosity, and hydraulic conductivity can be effectively modeled as random space functions. The flow through such a stochastically parametrized medium is hence itself also a random velocity field.

Many of the problems of interest have, in addition, interacting particles moving within the flows. A good example are problems of colloid formation and related issues of colloid stability and transport in a porous medium. These advected particles can interact chemically or through coagulation (aggregation) and disaggregation, so that the particle sizes range from monomers to large polymer clusters. The nonlinear processes of aggregation/disaggregation are described by the Smoluchowski equation in the inhomogeneous case governing the coagulation of particles dispersed by a velocity field $ {\bf v} (t,x)$:

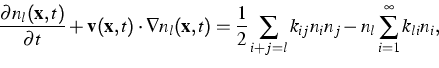
\begin{displaymath} \frac {\partial n_l( {\bf x} ,t)} {\partial t}+ {\bf v} ( {\... ...its_{i+j=l}k_{ij}n_in_j -n_l\sum\limits_{i=1}^\infty k_{li}n_i,\end{displaymath}

where $n_l( {\bf x} ,t)$ is the concentration of clusters of size l, $l=1,2,\ldots~$at a point $ {\bf x} $ at time t; $ {\bf v} ( {\bf x} ,t)$ is the velocity of the host gas, $k_{ij}=k_{ij}( {\bf x} ,t)$ is the coagulation coefficient. It is supposed that the initial size distribution is given: $n_l( {\bf x} ,0)=n_l^0( {\bf x} )$.

Hence, it is natural to consider using probabilistic models for the particle transformation and transport thus further motivating the construction of unified Monte Carlo algorithms for both the particle-particle and particle-fluid interactions. We suggested new stochastic algorithms for the inhomogeneous case in [7], [13], [25] and developed them further in [31].

In the porous media transport, only one type of stochastic models was used, namely, the random displacement method (RDM) for hydrodynamic dispersion equations. It should be stressed that RDM can be applied only if the displacement covariance tensor is known (e.g., from measurements, or numerical simulations), and cannot be applied if the functionals of interest are evaluated at times comparable with the characteristic correlation scale of the flow. In contrast, the Lagrangian stochastic models based on the tracking particles in a random velocity field extracted from the numerical solution of the flow equation (for brevity, we will call this model DSM, the direct simulation method) are free of these limitations, but the computational resources required are vast. Therefore, it is quite suggestive to construct a Langevin-type stochastic model which is an approximation to DSM, and is written in the form of a stochastic differential equation for the position and velocity. The basis for the Langevin-type approach comes from the Kolmogorov similarity theory of fully developed turbulence saying that the velocity structure tensor is a linear function in time which is universal in the inertial subrange. The linearity is the necessary condition to derive a Langevin-type equation to mimic the behavior of the real Lagrangian trajectories. Therefore, the crucial point is here to see if in the porous media this kind of linear law can be observed. We studied this problem by using the DSM, and detailed numerical simulations and comparisons with the random displacement model were carried out before we have constructed this Langevin-type model as a powerful instrument for practical calculations. Special small perturbation analysis is made in the case of small velocity fluctuations when the Gaussian velocity field is simulated directly through randomized spectral representation [8].

The work is done in cooperation with Université Libre de Bruxelles and FZ Jülich, Institut für Chemie und Dynamik der Geosphäre. The results are presented in [14], [29], [31].

5. Numerical methods for stochastic Hamiltonian systems and Langevin-type equations based on symplectic integrators. Stability problems of stochastic dynamics

(G.N. Milstein).

In general we face many difficulties when implementing numerical methods for stochastic differential equations. At the same time, methods adapted to specific systems can be more efficient than general methods. In [21], [23] and [24], specific methods for stochastic Hamiltonian systems and Langevin-type equations are proposed. Stochastic Hamiltonian systems, like deterministic Hamiltonian systems, possess the property of preserving the symplectic structure. For instance, Hamiltonian systems with additive noise are a rather wide and important class of equations having this property. A lot of attention has been paid to symplectic integration of deterministic Hamiltonian systems. This interest is motivated by the fact that symplectic integrators in comparison with usual numerical schemes allow to simulate Hamiltonian systems on very long time intervals with high accuracy. Symplectic methods for stochastic Hamiltonian systems, as proposed in [23], [24], have significant advantages over standard schemes for stochastic differential equations as well. We construct symplectic methods for general stochastic Hamiltonian systems as well as higher-order symplectic schemes for Hamiltonian systems with separable Hamiltonians, Hamiltonian systems with additive and colored noise, Hamiltonian systems with small noise, etc.

It is natural to expect that numerical methods which, in a sense, are close to symplectic ones, also have advantages when applied to stochastic systems close to Hamiltonian ones. An important and large class of such systems is given by Langevin-type equations. The Langevin-type equations are met in models from physics, chemistry, and biology. In [21] we construct special numerical methods (called quasi-symplectic) which preserve certain properties of Langevin-type equations. These methods degenerate to symplectic ones when the system degenerates to a Hamiltonian one, and their law of phase volume contractivity is close to the exact one. Numerical tests of both symplectic and quasi-symplectic methods clearly demonstrate superiority of the proposed methods over standard ones on very long time intervals.

Stability properties of stochastic systems are studied in  [6], [17]. Much effort has been devoted to the stability analysis of stationary points for linear autonomous systems of stochastic differential equations

In  [17], we introduce the notions of Lyapunov exponent, moment Lyapunov exponent, and stability index for linear non-autonomous systems with periodic coefficients. We study these problems extensively for second-order conservative systems with small random and periodic excitations and obtain an asymptotic expansion of the moment Lyapunov exponent. As an application we consider the Hill and Mathieu equations with random excitations.

In [20], several random walks for the general Dirichlet problem for multi-dimensional linear elliptic and parabolic partial differential equations are proposed. They are constructed on the basis of weak approximations for the characteristic system of stochastic differential equations due to the corresponding probabilistic representations of the solution to a corresponding boundary value problem. The methods of [20] are the simplest among methods of order O(h), because inside the domain we use the Euler weak approximations and near the boundary we exploit linear interpolation. In addition, these methods have a layer structure, and, in particular, the one-step method of numerical integration can be used. Therefore it is possible to apply extrapolation methods. As a result we suggest a number of efficient Monte Carlo algorithms.

For evaluating a hedging strategy against a multi-asset European claim we have to know at every moment the solution of the Cauchy problem for the corresponding linear parabolic equation (the value of the hedging portfolio) and its derivatives (the deltas). In [19], we suggest to find these quantities by Monte Carlo simulation of the corresponding system of stochastic differential equations using weak solution schemes.

Nonlinear PDEs usually do not have analytic solutions and are mostly investigated by numerical methods, which are traditionally based on deterministic approaches. A probabilistic approach to constructing new numerical methods for solving the Cauchy problem for nonlinear parabolic partial differential equations is developed in [18]. The approach is based on making use of the well-known probabilistic representations of solutions to linear partial differential equations and ideas of numerical integration of stochastic differential equations in the weak sense. Despite their probabilistic nature these methods are nevertheless deterministic. The probabilistic approach takes into account a coefficient dependence on the space variables and a relationship between diffusion and advection terms in an intrinsic manner. In particular, the derived layer methods allow to avoid difficulties stemming from essentially changing coefficients and strong advection. The numerical algorithms are tested using computer experiments, among them tests on the Burgers equation with small viscosity and the Kolmogorov-Petrovskij-Piskunov (KPP) equation. Results are in good agreement with theory. We also present a comparison analysis of the layer methods and the well-known finite-difference schemes, demonstrating some of the advantages of the proposed methods. The approach is also applied to the numerical solution of the Neumann problem for nonlinear parabolic equations in [22] and to Navier-Stokes equations in [1].

References:

  1. YA. BELOPOLSKAYA, G.N. MILSTEIN, An approximation method for Navier-Stokes equations based on probabilistic approach, WIAS Preprint no. 733, 2002.
  2. G. DAGAN, Flow and Transport in Porous Formations, Springer, New York, 1989.
  3. C. ENGELHARDT, O. KURBANMURADOV, K.K. SABELFELD, A. SUKHODOLOV, Numerical study of the statistical characteristics of the mixing processes in rivers, WIAS Preprint no. 705, 2001.
  4. L.W. GELHAR, Stochastic Subsurface Hydrology, Prentice Hall, New Jersey, 1993.
  5. T.K. FLESCH, J.D. WILSON, A two-dimensional trajectory-simulation model for non-Gaussian, inhomogeneous turbulence within plant canopies, Boundary-Layer Meteorology, 61 (1992), pp. 349-374.
  6. P. IMKELLER, G.N. MILSTEIN, Moment Lyapunov exponent for conservative systems with small periodic and random perturbations, Stochastics Dynamics, 2 (2002), pp. 25-48.
  7. A.A. KOLODKO, K.K. SABELFELD, Stochastic Lagrangian model for spatially inhomogeneous Smoluchowski equation governing coagulating and diffusing particles, WIAS Preprint no. 689, 2001, Monte Carlo Meth. Appl., 7 (2001), pp. 223-228.
  8. D. KOLYUKHIN, K.K. SABELFELD, Stochastic Eulerian model of transport in porous medium, to appear in: Monte Carlo Meth. Appl.
  9. O. KURBANMURADOV, K.K. SABELFELD, Lagrangian stochastic models for turbulent dispersion in the atmospheric boundary layer, Boundary-Layer Meteorology, 97 (2000), pp. 191-218.
  10. O. KURBANMURADOV, K.K. SABELFELD, P.K. YEUNG, Analysis of relative dispersion of two particles by Lagrangian stochastic models and DNS methods, Monte Carlo Meth. Appl., 7 (2001), pp. 245-264.
  11. O. KURBANMURADOV, Ü. Rannik, K.K. SABELFELD, T. VESALA, Estimation of mean concentration and fluxes by Lagrangian stochastic models, Math. Comput. Simulation, 54 (2001), pp. 459-476.
  12. \dito , Direct and adjoint Monte Carlo for the footprint problem, Monte Carlo Meth. Appl., 5 (1999), pp. 85-111.
  13. O. KURBANMURADOV, K.K. SABELFELD, Coagulation of aerosol particles in intermittent turbulent flows, Monte Carlo Meth. Appl., 6 (2000), pp. 211-253.
  14. O. KURBANMURADOV, K.K. SABELFELD, O. SMIDTS, H. VEREECKEN, A Lagrangian stochastic model for transport in statistically homogeneous porous media, WIAS Preprint no. 786, 2002.
  15. O. KURBANMURADOV, K.K. SABELFELD J.G.M. SCHOENMAKERS, Lognormal approximations to LIBOR market models, J. Comput. Finance, 6 (2002), pp. 69-100.
  16. O. KURBANMURADOV, Ü. Rannik, K.K. SABELFELD, T. VESALA, Stochastic Lagrangian footprint calculations for horizontally inhomogeneous surface roughness, to appear as WIAS Preprint.
  17. G.N. MILSTEIN, The asymptotic behavior of semi-invariants for linear stochastic systems, Stochastics Dynamics, 2 (2002), pp. 281-294.
  18. \dito , The probability approach to numerical solution of nonlinear parabolic equations, Numer. Methods Partial Differential Equations, 18 (2002), pp. 490-522.
  19. G.N. MILSTEIN, J.G.M. SCHOENMAKERS, Numerical construction of hedging strategies against multi-asset European claims, Stochastics Stochastics Rep., 73 (2002), pp. 125-157.
  20. G.N. MILSTEIN, M.V. TRETYAKOV, The simplest Random Walks for the Dirichlet problem, Theory Probab. Appl., 47 (2002), pp. 39-58.
  21. \dito , Numerical methods for Langevin-type equations based on symplectic integrators, WIAS Preprint no. 727, 2002.
  22. \dito , A probabilistic approach to the solution of the Neumann problem for nonlinear parabolic equations, IMA J. Numer. Anal., 22 (2002), pp. 599-622.
  23. G.N. MILSTEIN, YU.M. REPIN, M.V. TRETYAKOV, Symplectic integration of Hamiltonian systems with additive noise, SIAM J. Numer. Anal., 39 (2002), pp. 2066-2088.
  24. \dito , Numerical methods for stochastic systems preserving symplectic structure, SIAM J. Numer. Anal., 40 (2003), pp. 1583-1604.
  25. A.A. ONISCHUK, A.I. LEVYKIN, V.P. STRUNIN, K.K. SABELFELD, V.N. PANFILOV, Aggregate formation under homogeneous Silane thermal decomposition, J. Aerosol Science, 31 (2000), pp. 1263-1281.
  26. Ü. Rannik, M.  AUBINET, O. KURBANMURADOV, K.K. SABELFELD, T. MARKKANEN, T.  VESALA, Footprint analysis for measurements over a heterogeneous forest, Boundary-Layer Meteorology, 97 (2000), pp. 137-166.
  27. K.K. SABELFELD, Monte Carlo Methods in Boundary Value Problems, Springer, Heidelberg, New York, Berlin, 1991.
  28. K.K. SABELFELD, I.A. SHALIMOVA, Random Walk on spheres methods for iterative solution of elasticity problems, Monte Carlo Meth. Appl., 8 (2002) pp. 171-202.
  29. K.K. SABELFELD, Stochastic Lagrangian models for simulation of particle transport in porous media, in: Bulletin of Institute of Computational Mathematics and Mathematical Geophysics, Russian Academy of Sciences, Novosibirsk, 2002, pp. 264-269.
  30. K.K. SABELFELD, I.A.SHALIMOVA, Decentered Random Walk on spheres for static elasticity problems, in: Bulletin of Institute of Computational Mathematics and Mathematical Geophysics, Russian Academy of Sciences, Novosibirsk, 2002, pp. 270-275.
  31. K.K. SABELFELD, A.A. KOLODKO, Stochastic Lagrangian models and algorithms for spatially inhomogeneous Smoluchowski equation, Math. Comput. Simulation, 61 (2003), pp. 113-137.
  32. K.K. SABELFELD, I.A. SHALIMOVA, Spherical Means for PDEs, VSP, Utrecht, The Netherlands, 1997.
  33. K.K. SABELFELD, N.A. SIMONOV, The Random Walks on Boundary for Solving PDEs, VSP, Utrecht, The Netherlands, 1994.
  34. K.K. SABELFELD, I.A. SHALIMOVA, Random Walk on spheres methods and iterative solutions of elasticity problems, WIAS Preprint no. 704, 2001.
  35. \dito , Forward and backward stochastic Lagrangian models for turbulent transport and the well-mixed condition, Monte Carlo Meth. Appl., 7 (2001), pp. 369-382.
  36. A. SUKHODOLOV, O. KURBANMURADOV, C. ENGELHARDT, K.K. SABELFELD, On characteristic scales of transport and mixing processes in rivers. Part II: Turbulence and mixing, in press in: Water Resources Research.


 [Next]:  Research Group Continuum Mechanics  
 [Up]:  Project descriptions  
 [Previous]:  Applied mathematical finance  
 [Contents]   [Index] 

LaTeX typesetting by I. Bremer
5/16/2003