[Next]:

Applied mathematical finance

[Up]:

Project descriptions

[Previous]:

Project descriptions

 [Contents] 

 [Index] 

Subsections

• 1. Adaptive smoothing
• 2. Dimension reduction
• 3. Goodness-of-fit and model check
• 4. Cluster analysis, multivariate graphics, data mining
• 5. Ill-posed inverse problems

Statistical data analysis

Collaborator: V. Essaoulova , A. Hutt , S. Jaschke , P. Mathé , H.-J. Mucha , J. Polzehl , V. Spokoiny .

Cooperation with: F. Godtliebsen (University of Tromsø, Norway), G. Torheim (Amersham Health, Oslo, Norway), S. Sardy (Swiss Federal Institute of Technology (EPFL) Lausanne, Switzerland), A. Juditski (Université de Grenoble, France), M. Hristache (ENSAI, Rennes, France), W. Härdle (SFB 373, Humboldt-Universität zu Berlin), J. Horowitz (Northwestern University, Chicago, USA), S. Sperlich (University Carlos III, Madrid, Spain), D. Mercurio (Humboldt-Universität zu Berlin), I. Grama (Université de Bretagne-Sud, Vannes, France), C. Vial-Roget (ENSAI, Rennes, France), A. Goldenshluger (University of Haifa, Israel), Y. Xia (Cambridge University, UK), O. Bunke, B. Droge and H. Herwartz (SFB 373, Humboldt-Universität zu Berlin), H.-G. Bartel (Humboldt-Universität zu Berlin), R. Brüggemann (Institut für Gewässerökologie und Binnenfischerei, Berlin), J.  Dolata (Johann Wolfgang Goethe-Universität Frankfurt am Main), U. Simon (Institut für Gewässerökologie und Binnenfischerei, Berlin), P. Thiesen (Universität der Bundeswehr Hamburg), O. Lepski and Yu. Golubev (Université de Marseille, France), A. Samarov (Massachusetts Institute of Technology, Cambridge, USA), S.V. Pereverzev (National Academy of Sciences of Ukraine, Kiev), R. von Sachs (Université Louvain-la-Neuve, Belgium), S. Zwanzig (Uppsala University, Sweden), B. Röhl-Kuhn (Bundesanstalt für Materialforschung und -prüfung (BAM) Berlin)

Supported by: BMBF: ``Effiziente Methoden zur Bestimmung von Risikomaßen'' (Efficient methods for the valuation of risk measures)
DFG: DFG-Forschungszentrum ``Mathematik für Schlüsseltechnologien'' (Research Center ``Mathematics for Key Technologies''); SFB 373 ``Quantifikation und Simulation Ökonomischer Prozesse'' (Quantification and simulation of economic processes), Humboldt-Universität zu Berlin; Priority Program 1114 ``Mathematische Methoden der Zeitreihenanalyse und digitalen Bildverarbeitung'' (Mathematical methods for time series analysis and digital image processing)

Description:

The theoretical basis of the project Statistical data analysis are modern nonparametric statistical methods designed to model and analyze complex structures. WIAS has, with main mathematical contributions, become an authority in this field including its applications to problems in technology, medicine and environmental research as well as risk evaluation for financial products.

Methods developed in the institute within this project area can be grouped into the following main classes.

1. Adaptive smoothing

(V. Essaoulova, A. Hutt, J. Polzehl, V. Spokoiny).

The studies of adaptive smoothing methods have mainly been motivated by applications to medical imaging, especially in the context of dynamic and functional Magnet Resonance Imaging (dMRI and fMRI), and the analysis of high-frequency financial time series. Research on imaging problems is carried out within the DFG Research Center ``Mathematics for Key Technologies'' and the DFG Priority Program 1114 ``Mathematical methods for time series analysis and digital image processing''. Modeling of local stationary time series is based on cooperation within the SFB 373 ``Quantification and simulation of economical processes'' at Humboldt University of Berlin and the BMBF project ``Efficient methods for the valuation of risk measures''. Cooperation also exists with G. Torheim (Amersham Health, Oslo, Norway) and F. Godtliebsen (University of Tromsø, Norway) for the analysis of dMRI experiments.

Two main approaches have been proposed and investigated, a pointwise adaptive approach and adaptive weights smoothing. The pointwise adaptive approach was developed in [37] for estimation of regression functions with discontinuities. [29] extended this method to smoothing of 2D images. The procedure delivers an optimal (in rate) quality of edge recovering and demonstrates a reasonable numerical performance. Other interesting applications of this approach include the analysis of time-varying and local stationary time series and tail index estimation. [25] develop a pointwise adaptive approach for volatility modeling of financial time series. [9] extends this procedure to the case of multi-dimensional financial time series. Appropriate methods for local stationary time series are investigated in [6] and [7]. [5] propose a new method of adaptive estimation of the tail index of a distribution by reducing the original problem to the inhomogeneous exponential model and applying the pointwise adaptive estimation procedure. Although the pointwise adaptive procedure turns out to be asymptotically efficient, its computational complexity is high and results for finite sample sizes are less promising than for the other method called adaptive weights smoothing .

The adaptive weights smoothing approach has been proposed in [30] in the context of image denoising. The general idea behind the adaptive weights smoothing procedure is structural adaptation. The procedure attempts in an iterative way to recover the unknown local structure from the data and to utilize the obtained structural information for improving the quality of estimation. The procedure possesses a number of remarkable properties like preservation of edges and contrasts and nearly optimal noise reduction inside large homogeneous regions. It is also dimension-free and applies in high-dimensional situations. The original procedure designed for the local constant regression model has been thoroughly revised and generalized to a wide variety of models. Results have been presented at several conferences and are contained in [32, 33]. [32] describes how the AWS procedure can be used for estimation of piecewise smooth curves or manifolds by local polynomial approximation.

Fig. 1: Original (left), image with additive noise (central) and AWS reconstruction (right)

Figure 1 illustrates the result of a local quadratic fit of a discontinuous 2D regression surface. The left image gives the true function, the central image contains the noisy image while the right image provides the reconstruction.

[33] describes an extension of the AWS method to local likelihood estimation for exponential family models with varying parameters as well as applications to various particular problems. Important model classes include Poisson regression, binary response models, volatility models and exponential models. Applications are given for the following problems:

• Analysis of fMRI and dMRI experiments: Adaptive weights smoothing allows for the analysis of spatio-temporal structures. The methods proposed in [31] have been tested on dMRI datasets from cardiology. We are currently revising the vectorized procedures based on the generalizations described in [32, 33].
• Positron emission tomography data can be successfully described by the Poisson model with varying intensity. Figure 2 illustrates the results for a preliminary experiment using the Vard-Shepp-Kaufman phantom [42].

  
  

  Fig. 2: Original phantom (left), image with Poisson noise (central) and AWS reconstruction from the noisy image (right)

  

  
  
  
  
• Density estimation: An adaptive weights procedure for density estimation has been obtained using the asymptotic equivalence of density estimation and Poisson regression.
• Classification: Nonparametric classification can be approached using the binary response model. The resulting method improves on nearest-neighbor rules and nonadaptive kernel smoothing.

  
  

  Fig. 3: Bayesian classification rule (left), and classification rules obtained by k-NN, AWS and kernel smoothing

  

  
  
  
  

  Figure 3 illustrates the classification results obtained for an artificial discriminant analysis problem used in [10] for the adaptive weights, nearest-neighbor and kernel approach using optimal smoothing parameters in the last two methods.

• Time-inhomogeneous time series and volatility estimation: Time series models with varying coefficients are appropriate for a wide range of financial time series and biometric signals. An adaptive weights smoothing for AR- and ARCH-models with time-varying coefficients is under development.

  
  

  Fig. 4: Inhomogeneity of the volatility of the DM / US $ exchange rate

  

  
  
  
  

  Figure 4 illustrates an analysis of the DM / US $ exchange rate (data are (C) 2001 by Prof. W. Antweiler University of British Columbia, Vancouver BC, Canada, and have been obtained from the Pacific Exchange Rate Service http://pacific.commerce.ubc.ca/xr/data.html). Displayed are the returns $\, \vert R_t\vert \,$ and estimates of the volatility $\, \sigma_{t} \,$obtained by the symmetric and asymmetric version of AWS for the time period from January 1993 to December 1997.

• Tail index estimation: The tail index is used to characterize the tail behavior of a distribution. This is important, e.g., for extreme value statistics and risk assessment. [33] use the idea employed in [5] to obtain an adaptive weights method. The resulting estimate can be viewed as a generalization of the Hill estimator with an adaptive choice of its smoothing parameter.

2. Dimension reduction

(S. Jaschke, J. Polzehl, V. Spokoiny).

Many statistical applications are confronted with high-dimensional data. Typical examples are given by econometric or financial data. For instance, usual financial practice leads to monitoring about 1000 to 5000 different data processes. Single- and multi-index models are often used in multivariate analysis to avoid the so-called ``curse of dimensionality'' problem (high-dimensional data are very sparse). These models focus on index vectors or dimension reduction spaces which allow to reduce the dimensionality of the data without essential loss of information. They generalize classic linear models and can be viewed as a reasonable compromise between too restrictive linear and too vague pure nonparametric modeling. Indirect methods of index estimation like the nonparametric least-squares estimator, or nonparametric maximum likelihood estimator have been shown to be asymptotically efficient, but their practical applications are very restricted. The reason is that calculation of these estimators leads to an optimization problem in a high-dimensional space, see [18]. In contrast, direct methods like the average derivative estimator, or sliced inverse regression are computationally straightforward, but the corresponding results are far from being optimal, again due to the ``curse of dimensionality'' problem. Their theory applies only under very restrictive model assumptions, see [2], [34] and [40].

[16] developed a structural adaptive approach to dimension reduction using the structural assumptions of a single-index and multi-index model. These models are frequently used in econometrics to overcome the curse of dimensionality when describing the dependencies between variables in high-dimensional regression problems. The new methods allow for a more efficient estimation of the effective dimension reduction space characterizing the model and of the link function. [39] improves on these procedures for single- and multi-index models and generalizes it to the case of partially linear models and partially linear multi-index models.

Fig. 5: Projections into the estimated index space obtained by structural adaptation and by established competitors. Data follow a single-index model in a 20-dimensional regressor space.

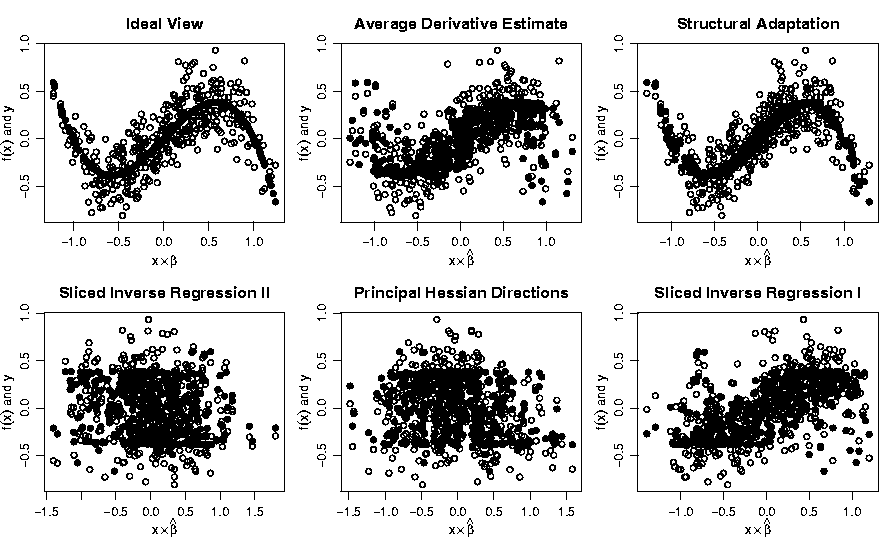
Figure 5 illustrates the quality of the estimated index in comparison to other established methods, i.e. a generalized average derivative estimate (ADE), sliced inverse regression (SIR) and principal Hessian directions (PHD), for a single-index model in a 20-dimensional space. [35] propose a new method to analyze a partially linear model whose nonlinear component is completely unknown. The target here is variable selection, i.e. the identification of the set of regressors which enter in a nonlinear way into the model. As a by-product the method allows to test the dimensionality of the nonlinear component.

Dimension reduction also turns out to be an essential component in the adaptive weights smoothing approaches to time-inhomogeneous time series in case of high dimensions of the parameter space. Methods to handle this problem are currently under investigation.

3. Goodness-of-fit and model check

(V. Spokoiny).

In many statistical data analyses, the use of simple models described by a finite number of parameters would be preferable. However, an application of parametric modeling has to be combined with a careful goodness-of-fit test. In other words, a statistician has to check whether the data really follow (or, at least, do not contradict) the parametric assumption. This check can be naturally formulated as the problem of testing a simple or parametrically specified hypothesis. The modern statistical theory focuses on developing tests which are sensitive (powerful) for a possibly large class of alternatives. The classical Neyman-Pearson theory considers the very narrow class of parametric alternatives. The classical nonparametric procedures like von Mises, $\, \chi^{2} \,$ or Kolmogorov-Smirnov have a serious drawback of being non-sensitive against a smooth wiggling alternative that typically arises in the goodness-of-fit problem. Optimal (in rate) nonparametric tests for such alternatives have been constructed by [17]. However, practical applications of such rate-optimal tests require to specify a smoothing parameter. A number of data-driven (adaptive) tests have been recently proposed in [3], [4], [19], among others. [36, 38] considered the problem of adaptive testing of a simple hypothesis for the ``ideal'' sequence space model against a smooth alternative and constructed an adaptive test which is optimal (in rate) in the class of such adaptive tests. [38] considered the case of a linear hypothesis for a regression model. [14] developed an adaptive rate-optimal test of a parametric hypothesis for a heterogeneous regression model. [15] extended the method and the results for the median regression model with an unknown possibly heterogeneous noise.

4. Cluster analysis, multivariate graphics, data mining

(H.-J. Mucha).

Cluster analysis, in general, aims at finding interesting partitions or hierarchies directly from the data without using any background knowledge. Here a partition P(I,K) is an exhaustive subdivision of the set of I objects (observations) into K non-empty clusters (subsets, groups) C_k that are pairwise disjoint. On the other hand a hierarchy is a sequence of nested partitions. Having data mining applications and improvement of stability of results in mind some new model-based cluster analysis tools are under development. For example, clustering techniques based on cores can deal with both huge data sets and outliers, or, intelligent clustering based on voting can find usually much more stable solutions. A core is a dense region in the high-dimensional space that, for example, can be represented by its most typical observation, by its centroid or, more generally, by assigning weight functions to the observations. Almost all techniques of high-dimensional data visualization (multivariate graphics, projection techniques) can also take into account weighted observations. As an application in the field of water ecology, a result from model-based Gaussian clustering is presented in the figure below. The data under investigation comes from a snapshot of monitoring of phytoplankton.

Fig. 6: Extract of a scatterplot matrix of cluster membership (data: flow cytometry measurements)

Model-based as well as heuristic clustering techniques are part of our statistical software ClusCorr98^®. Moreover we offer multivariate visualization techniques like principal components analysis or correspondence analysis as well as other exploratory data analysis. ClusCorr98^® uses the Excel spreadsheet environment and its database connectivity.

5. Ill-posed inverse problems

(P. Mathé, V. Spokoiny).

Ill-posed equations arise frequently in the context of inverse problems, where it is the aim to determine some unknown characteristics of a physical system from data corrupted by measurement errors. Work in this direction is carried out in cooperation with the project Numerical methods for inverse problems and nonlinear optimization of the WIAS research group ``Nonlinear Optimization and Inverse Problems'' and with S.V. Pereverzev, Kiev.

We study problems

$$y_\delta= A x + \delta\xi,$$

or their discretizations

$$y_{\delta,i}=\langle y_\delta,\varphi_i\rangle = \langle Ax,\varphi_i\rangle + \delta\xi_i,\quad i=1,\dots,n,$$

where A acts injectively and compact in some Hilbert space, and $\delta\gt$ describes the noise level of the data $y_{\delta,i}$.

Modern numerical analysis has developed a rich apparatus, which reflects different aspects of the sensitivity of ill-posed problems. In Hilbert scales such problems were systematically analyzed since Natterer [28]. Sometimes, this restriction does not give a flexible approach to estimating realistic convergence rates. Moreover, some important cases are not covered by the ordinary Hilbert scale theory. One interesting example is given in [1] which studies an inverse problem in optical diffraction.

For these reasons variable Hilbert scales were introduced by Hegland [11] and further developed in [12] and [41]. Within this framework the solution smoothness is expressed in terms of so-called general source conditions, given by some function over the modulus of the operator A involved in the ill-posed equation. These allow to describe local smoothness properties of the solution. Our research was carried out in the following directions.

-

[22] presents the mathematical foundation of regularization of ill-posed problems in variable Hilbert scales.

-

The other aspect concerns discretization. [23] extends the approach from [21] to projection methods in variable Hilbert scales.

-

An adaptive strategy, which automatically provides the optimal order of accuracy for a wide range of source conditions is given in [22] and [23].

-

The analysis was extended to statistically ill-posed problems in variable Hilbert scales in [24].

[8] studied one special statistical inverse problem of reconstructing a planar convex set from noisy observations of its moments. An estimation method based on pointwise recovering of the support function of the set has been developed. It is shown that the proposed estimator is near-optimal in the sense of the order of convergence. An application to tomographic reconstruction is discussed, and it is indicated how the proposed estimation method can be used for recovering edges from noisy Radon data.

References:

1. G. BRUCKNER, J. ELSCHNER, M. YAMAMOTO, An optimization method for grating profile reconstruction,
   WIAS Preprint no. 682, 2001.
2. N. DUAN, K.-C. LI, Slicing regression: A link-free regression method, Ann. Statist., 19 (1991), pp. 505-530.
3. R.L. EUBANK, J.D. HART, Testing goodness-of-fit in regression via order selection criteria, Ann. Statist., 20 (1992), pp. 1424-1425.
4. J. FAN, Test of significance based on wavelet thresholding and Neyman's truncation, J. Amer. Statist. Assoc., 91 (1996), pp. 674-688.
5. I. GRAMA, V. SPOKOINY, Tail index estimation by local exponential modelling, manuscript.
6. M. GIURCANU, V. SPOKOINY, Confidence estimation of the covariance function of stationary and locally stationary processes, WIAS Preprint no. 726, 2002, to appear in: J. Time Ser. Anal.
7. M. GIURCANU, V. SPOKOINY, R. VON SACHS, Pointwise adaptive modeling of locally stationary time series, manuscript in preparation.
8. A. GOLDENSHLUGER, V. SPOKOINY, On the shape-from-moments problem and recovering edges from noisy Radon data, manuscript.
9. W. HÄRDLE, H. HERWARTZ, V. SPOKOINY, Time inhomogeneous multiple volatility modelling, to appear in: J. Financial Econometrics.
10. T.J. HASTIE, R.J. TIBSHIRANI, J. FRIEDMAN, The Elements of Statistical Learning, Springer, New York, 2001.
11. M. HEGLAND, An optimal order regularization method which does not use additional smoothness assumptions, SIAM J. Numer. Anal., 29 (1992), pp. 1446-1461.
12. , Variable Hilbert scales and their interpolation inequalities with applications to Tikhonov regularization, Appl. Anal., 59 (1995), pp. 207-223.
13. T. HOHAGE, Regularization of exponentially ill-posed problems, Numer. Funct. Anal. Optim., 21 (2000), pp. 439-464.
14. J.L. HOROWITZ, V. SPOKOINY, An adaptive, rate-optimal test of a parametric mean regression model against a nonparametric alternative, Econometrica, 69 (2001), pp. 599-631.
15. , An adaptive rate-optimal test of linearity for median regression model, J. Amer. Statist. Assoc., 97 (2002), pp. 822-835.
16. M. HRISTACHE, A. JUDITSKY, J. POLZEHL, V. SPOKOINY, Structure adaptive approach for dimension reduction, Ann. Statist., 29 (2001), pp. 1537-1566.
17. YU.I. INGSTER, Asymptotically minimax hypothesis testing for nonparametric alternatives. I-III., Math. Methods Statist., 2 (1993), pp. 85-114; 3 (1993), pp. 171-189; 4 (1993), pp. 249-268.
18. R.L. KLEIN, R.H. SPADY, An efficient semiparametric estimator for binary response models, Econometrica, 61 (1993), pp. 387-421.
19. T. LEDWINA, Data-driven version of Neyman's smooth test of fit, J. Amer. Statist. Assoc., 89 (1994), pp. 1000-1005.
20. O.V. LEPSKII, A problem of adaptive estimation in Gaussian white noise, Teor. Veroyatnost. i Primenen., 35 (1990), pp. 459-470.
21. P. MATHÉ, S.V. PEREVERZEV, Optimal discretization of inverse problems in Hilbert scales. Regularization and self-regularization of projection methods, SIAM J. Numer. Anal., 38 (2001), pp. 1990-2021.
22. , Geometry of ill-posed problems in variable Hilbert scales, manuscript, 2002.
23. , Discretization strategy for ill-posed problems in variable Hilbert scales, manuscript, 2002.
24. , Optimal error of ill-posed problems in variable Hilbert scales under the presence of white noise in variable Hilbert scales, manuscript, 2002.
25. D. MERCURIO, V. SPOKOINY, Statistical inference for time-inhomogeneous volatility models, to appear in: Ann. Statist.
26. H.-J. MUCHA. H.-G. BARTEL, J. DOLATA, Core-based clustering techniques, to appear in: Proc. 26th Annual Conference of the GfKl, Springer, Heidelberg.
27. H.-J. MUCHA, An intelligent clustering technique based on voting, to appear in: Proc. Int. Conf. on Modeling and Simulating of Complex System, Chengdu, China.
28. F. NATTERER, Error bounds for Tikhonov regularization in Hilbert scales, Appl. Anal., 18 (1984), pp. 29-37.
29. J. POLZEHL, V. SPOKOINY, Image denoising: Pointwise adaptive approach, to appear in: Ann. Statist., 31 (2003), No. 2.
30. , Adaptive weights smoothing with applications to image restoration, J. Roy. Statist. Soc. Ser. B, 62 (2000), pp. 335-354.
31. , Functional and dynamic Magnetic Resonance Imaging using vector adaptive weights smoothing, J. Roy. Statist. Soc. Ser. C, 50 (2001), pp. 485-501.
32. , Varying coefficient regression modeling by adaptive weights smoothing, manuscript in preparation.
33. , Local likelihood modeling by adaptive weights smoothing, WIAS Preprint no. 787, 2002.
34. L.J. POWELL, J.M. STOCK, T.M. STOKER, Semiparametric estimation of index coefficients, Econometrica, 57 (1989), pp. 1461-1481.
35. A. SAMAROV, V. SPOKOINY, C. VIAL, Component identification and estimation in nonlinear high-dimensional regression, manuscript in preparation.
36. V. SPOKOINY, Adaptive hypothesis testing using wavelets, Ann. Statist., 24 (1996), pp. 2477-2498.
37. , Estimation of a function with discontinuities via local polynomial fit with an adaptive window choice, Ann. Statist., 26 (1998), pp. 1356-1378.
38. , Data driven testing the fit of linear models, Math. Methods Statist., 10 (2001), pp. 465-497.
39. V. SPOKOINY, Y. XIA, Effective dimension reduction by structural adaptation, manuscript in preparation.
40. T.M. STOKER, Consistent estimation of scaled coefficients, Econometrica, 54 (1986), pp. 1461-1481.
41. U. TAUTENHAHN, Optimality for ill-posed problems under general source conditions, Numer. Funct. Anal. Optim., 19 (1998), pp. 377-398.
42. Y. VARDI, A.L. SHEPP, L. KAUFMAN, A statistical model for positron emission tomography, J. Amer. Statist. Assoc., 14 (1985), pp. 8-37.

[Next]:

Applied mathematical finance

[Up]:

Project descriptions

[Previous]:

Project descriptions

 [Contents] 

 [Index]