Probabilistic Cellular Automata

[Next]:

Finite and infinite dimensional systems of

[Up]:

Project descriptions

[Previous]:

Interacting catalytic branching processes

[Contents]

[Index]

Probabilistic Cellular Automata

Collaborator: S. Roelly

Cooperation with: P. Dai Pra (Università degli Studi di Padova, Italy), P.-Y. Louis (Berliner Graduiertenkolleg ``Stochastische Prozesse und Probabilistische Analysis'' (Graduate College ``Stochastic Processes and Probabilistic Analysis''), Université Lille 1, France)

Description:

Description: Stochastic processes called Probabilistic Cellular Automata, and denoted by PCA, are discrete-time Markov chains with parallel updating (see, e.g., [1], [3], [6]). PCA models are useful in a large number of scientific areas, for example for parallel computing.

In [2], the authors present some links between the sets of reversible and stationary and Gibbs measures, respectively for general PCAs. They illustrate these results on the following particular class ${\cal C}$ of reversible PCAs with transition probability P:

$\begin{displaymath} P(d\sigma/\eta) = \otimes_{k \in \IZ^d} p_k (d\sigma_k / \et... ...(\sigma_k)_k \in \{-1,+1\}^{\IZ^d}, \eta \in \{-1,+1\}^{\IZ^d} \end{displaymath}$

where

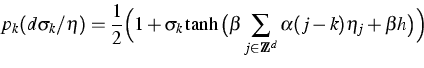
$\begin{displaymath} p_k (d\sigma_k / \eta) = \frac{1}{2} \Big(1+\sigma_k \tanh\b... ...beta \sum_{j \in \IZ^d} \alpha(j-k) \eta_j +\beta h\big)\Big)\end{displaymath}$

and the interaction $\alpha$ is of finite range.
In particular, they prove, using contour arguments that, for sufficiently small values of the temperature parameter $\frac{1}{\beta}$ , phase transition occurs, that is, there are several Gibbs measures associated to the multibody potential $\phi$ defined by:

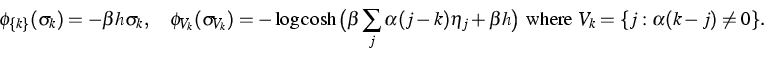
$\begin{displaymath} \phi_{\{k\}}(\sigma_k)=-\beta h \sigma_k, \quad \phi_{V_k}(\... ...j +\beta h\big)\text{ where } V_k= \{j : \alpha(k-j) \neq 0\}.\end{displaymath}$

Some of these Gibbs measures are stationary for P, which ensures the non-ergodicity of this PCA.

In [4], [5], the author studies ergodic properties of PCAs of the class ${\cal C}$ . In particular, he shows that in the attractive case (i.e. when $\alpha\geq 0$ ), if the set of Gibbs measures associated to the potential $\phi$ is reduced to one element $\mu$ which is moreover weak mixing, then the PCA is ergodic, its equilibrium measure is $\mu$ , and the convergence holds exponentially fast. The proof is based on a specific monotone coupling of PCAs. The domain of validity for this exponential ergodicity of attractive PCAs seems to be optimal, since it is known that, in the particular case $\alpha(k)=1$ if |k|=1 and $\alpha = 0$ otherwise, for all temperature larger than the critical one the unique Gibbs measure is weak mixing.

References:

D.A. DAWSON, Synchronous and asynchronous reversible Markov systems, Canad. Math. Bull., 17 (1974/75), pp. 633-649.
P. DAI PRA, P.-Y LOUIS, S. R $\oe$ lly, Stationary measures and phase transition for a class of Probabilistic Cellular Automata, ESAIM: Probability and Statistics, 6 (2002), pp. 89-104.
O. KOZLOV, N. VASILYEV, Reversible Markov chains with local interaction, in: Multicomponent Random Systems, R.L. Dobrushin, Y.G. Sinai, eds., Adv. Probab. Related Topics, 6, Dekker, New York, 1980, pp. 451-469.
P.-Y. LOUIS, Automates cellulaires probabilistes: mesures stationnaires, mesures de Gibbs associées et ergodicité, PhD thesis, Université Lille 1 and Politecnico di Milano, 2002.
$\dito$ ,Probabilistic Cellular Automata: Convergence towards equilibrium, in preparation.
J.L. LEBOWITZ, C. MAES, E.R. SPEER, Statistical mechanics of probabilistic cellular automata, J. Statist. Phys., 59 (1990), pp. 117-170