Optimization problems with random and nonsmooth

[Next]:

Regularization of severely ill-posed problems and

[Up]:

Project descriptions

[Previous]:

Direct and inverse diffraction problems in

[Contents]

[Index]

Optimization problems with random and nonsmooth data

Collaborator: R. Henrion

Cooperation with: W. Römisch (Humboldt-Universität (HU) zu Berlin), G. Wozny (Technische Universität (TU) Berlin), M. Steinbach (Konrad-Zuse-Zentrum für Informationstechnik Berlin (ZIB)), T. Szántai (Technical University of Budapest, Hungary), J. Outrata (Institute of Information Theory and Automation (UTIA) Prague, Czech Republic), A. Jourani (Université de Bourgogne, Dijon, France)

Supported by: DFG-Forschungszentrum ``Mathematik für Schlüsseltechnologien'' (Research Center ``Mathematics for Key Technologies'')

Description: Many applied optimization problems are subject to random and/or nonsmooth parameters in the data. This research project deals with modeling, development of solution procedures and investigations on the structure and stability of such problems. It is embedded into a cooperation with other scientific institutions in Berlin via DFG research projects (with HU and TU), the joint organization of a yearly course for chemical engineers supported by DECHEMA (with TU and ZIB) and a joint research seminar (with HU and ZIB).

The focus of research is on optimization problems with probabilistic constraints. There are two major applications considered in this context:

Optimization of a continuous distillation process under random inflow rate (previously supported DFG project);
Mean risk models for electricity portfolio management and stochastic programming (recently supported joint DFG project with W. Römisch, HU Berlin).

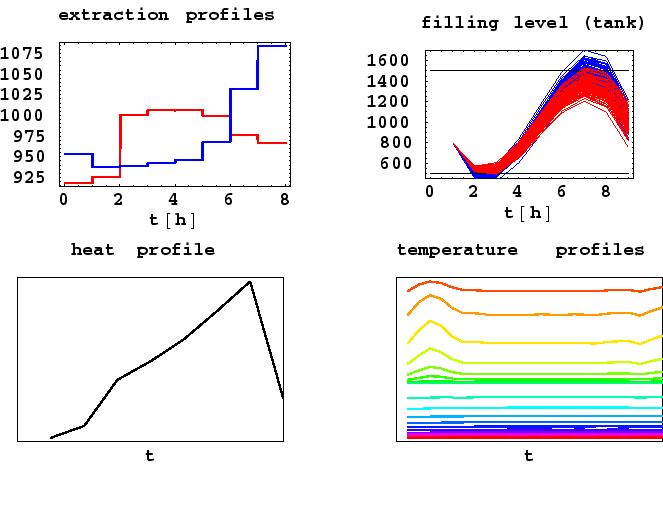
The key problem in the first application was to cope with random inflow rates of a methanol/ water mixture to a feed tank 1. A basic control variable is given by the rate of directing the mixture from the tank to the distillation column such that the undesired violation of upper and lower filling levels in the tank are avoided at high probability. Figure 1 illustrates a part of results obtained for a column with 20 trays driven at TU Berlin. It opposes the extraction profile obtained by probabilistic constraints (red) to that obtained by simple averaging of the inflow process (blue). As can be seen from the filling level profiles in the tank (based on 100 simulated inflow profiles), the safety of meeting the upper and lower level constraints (lines) can be drastically increased while the objective function (heat consumption) could be kept at the same value. The solution of the overall control problem is illustrated by a selected control variable (heat profile) and a selected state variable (temperature profiles in the twenty trays).

The recently initiated second application (joint project with W. Römisch, HU Berlin) addresses the extension of traditional expected revenue maximization in power engineering to mean-risk models. The main task is to identify suitable risk measures (e.g., [3], [4]) that fit from the algorithmic and stability point of view to the framework of solution methods in power management (e.g., [2]). One aspect to be considered here is the formulation of risk in terms of probabilistic constraints. Preliminary work in this direction has focused on the implementation of an algorithm for solving programs with polyhedral chance constraints (joint work with J. Bukszar, University of Miskolc and T. Szántai, Technical University of Budapest).

Both applications gave rise to theoretical investigations such as suitable approximations of probability measures or the structure of the feasible set in stochastic programming ([5], [6], [7]). The typically nonsmooth character of stochastic programs motivated to study the so-called calmness property of multifunctions which plays a fundamental role in the (nonsmooth) theory of first order necessary conditions, local error bounds, penalty methods, and weak sharp minima ([8], [9]).

Fig. 1: Results for the optimal control of a distillation process
$\ProjektEPSbildNocap {16cm}{fg4_hen.eps} \begin{imagesonly} \addtocounter{projektbild}{-1}\end{imagesonly}$

References:

R. HENRION, A. MÖLLER, Optimization of a continuous distillation process under random inflow rate, to appear in: Comput. Math. Appl.
N. GRÖWE-KUSKA, K.C. KIWIEL, M.P. NOWAK, W. RÖMISCH, I. WEGNER, Power management in a hydro-thermal system under uncertainty by Lagrangian relaxation, in: Decision Making under Uncertainty: Energy and Power, C. Greengard, A. Ruszczynski, eds., vol. 128 of IMA Vol. Math. Appl., Springer, New York, 2002, pp. 39-70.
H. FÖLLMER, A. SCHIED, Convex measures of risk and trading constraints, Finance and Stochastics, 6 (2002), pp. 429-447.
G. PFLUG, A. RUSZCZYNSKI, Risk measures for income streams, Stochastic Programming E-Print Series, 11 (2001).
R. HENRION, Structure and stability of probabilistic storage level constraints, in: Stochastic Optimization Techniques, K. Marti, ed., vol. 513 of Lecture Notes in Econom. and Math. Systems, Springer, Heidelberg, 2002, pp. 3-20.
$\dito$ , On the connectedness of probabilistic constraint sets, J. Optim. Theory Appl., 112 (2002), pp. 657-663.
R. HENRION, W. RÖMISCH, Hölder and Lipschitz stability of solution sets in programs with probabilistic constraints, WIAS Preprint no. 798, submitted.
R. HENRION, A. JOURANI, Subdifferential conditions for calmness of convex constraints, SIAM J. Optim., 13 (2002), pp. 520-534.
R. HENRION, A. JOURANI, J. OUTRATA, On the calmness of a class of multifunctions, SIAM J. Optim., 13 (2002), pp. 603-618.