|
|
|
[Contents] | [Index] |
Beschreibung der Forschungsarbeit: Sowohl in den industrierelevanten Projekten über Phasenübergänge als auch in den neu von Dreyer und Kunik entwickelten kinetischen Lösungen von Anfangs-Randwertproblemen hyperbolischer Systeme hat sich das Studium verschiedener Skalierungen von Zeit und Raum als derart bedeutsam erwiesen, dass sich hierfür mittlerweile ein eigenes Projekt herausgebildet hat.
Selbst bei ganz unterschiedlichen
Mikro-Makro-Übergängen
spielt das Skalenverhalten der resultierenden Makrosysteme bzgl. der
Zeit- und Ortsvariablen und anderer physikalischer Größen eine zentrale
Rolle. Wir erläutern dies an zwei Arten von Mikro-Makro-Übergängen
für Riemann'sche Anfangswertprobleme . In einem Beispiel ist die
Mikroebene durch die Newton'sche Mechanik des Vielteilchensystems eines
eindimensionalen atomaren Festkörpers beschrieben und im anderen Fall
durch die von Dreyer und Kunik in [1], [2] entwickelte
kinetische Lösung der gasdynamischen
Eulergleichungen
auf Zeitintervallen, die der mittleren Dauer des freien Fluges der Gasatome
entsprechen. In beiden Fällen resultieren makroskopische Systeme aus
Erhaltungsgleichungen, in denen nur noch die Massendichte ![]() , die
mittlere Geschwindigkeit v und die Temperatur T als Feldgrößen
auftreten. Für die atomare Kette erhalten wir für bestimmte
Anfangsdaten hyperbolische Gleichungssysteme, die reine Wellenausbreitungen
wie in Dreyer/Kunik [3] beschreiben, bzw. für das kinetische
Euler-Schema ein parabolisches Gleichungssystem zur Beschreibung der Wärmeleitung im Gas.
, die
mittlere Geschwindigkeit v und die Temperatur T als Feldgrößen
auftreten. Für die atomare Kette erhalten wir für bestimmte
Anfangsdaten hyperbolische Gleichungssysteme, die reine Wellenausbreitungen
wie in Dreyer/Kunik [3] beschreiben, bzw. für das kinetische
Euler-Schema ein parabolisches Gleichungssystem zur Beschreibung der Wärmeleitung im Gas.
a) Wir betrachten zunächst einen eindimensionalen Festkörper, der aus
einer Kette von Atomen aufgebaut ist. Die Atome mit Orten ![]() und Geschwindigkeiten
und Geschwindigkeiten ![]()
![]() , genügen den Newton'schen Bewegungsgleichungen
, genügen den Newton'schen Bewegungsgleichungen
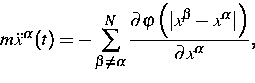 |
(3) |
Aus den Newton'schen Gleichungen wurden in [3] mit Hilfe
einer allgemeinen Fensterfunktion in Zeit und
Ort die folgenden allgemeinen
Erhaltungsgleichungen gewonnen, in denen sich alle auftretenden
thermodynamischen Makrogrößen wie ![]() , v, Druck p, innere
spezifische Energie u und der Wärmefluss q in eindeutiger Weise
durch Mittelwerte aus den Teilchentrajektorien im Träger der
Fensterfunktion darstellen lassen:
, v, Druck p, innere
spezifische Energie u und der Wärmefluss q in eindeutiger Weise
durch Mittelwerte aus den Teilchentrajektorien im Träger der
Fensterfunktion darstellen lassen:
Im Grenzfall unendlich großer Teilchenzahl ![]() zeigt sich dann eine entsprechende Riemannlösung, die invariant bzgl. der
folgenden Skalentransformation ist:
zeigt sich dann eine entsprechende Riemannlösung, die invariant bzgl. der
folgenden Skalentransformation ist:
| |
(4) |
Es wurde in [3] als Folge dieser Skaleninvarianz gezeigt,
dass dann nur lokale Gleichgewichtszustände in der Kette auftreten.
Diese werden durch orts- und zeitabhängige Verteilungen der
Zufallsvariablen ![]() beschrieben, wobei
beschrieben, wobei ![]() die Geschwindigkeit des Atoms
die Geschwindigkeit des Atoms ![]() ist und
ist und ![]() sein Abstand
vom rechten Nachbaratom. Je nach Art der Mikrobewegung ergeben sich dann
unterschiedliche Abschlussbedingungen, die u, p und q als
analytische Ausdrücke von
sein Abstand
vom rechten Nachbaratom. Je nach Art der Mikrobewegung ergeben sich dann
unterschiedliche Abschlussbedingungen, die u, p und q als
analytische Ausdrücke von ![]() und T liefern. Mit Hilfe dieser
Abschlussbedingungen konnten drei hyperbolische Feldgleichungssysteme
aus (2) explizit gewonnen werden, die zu qualitativ ganz
unterschiedlichen Gleichgewichtszuständen gehören und auch auf
unterschiedliche analytische Beziehungen für die spezifische Entropie
führen.
und T liefern. Mit Hilfe dieser
Abschlussbedingungen konnten drei hyperbolische Feldgleichungssysteme
aus (2) explizit gewonnen werden, die zu qualitativ ganz
unterschiedlichen Gleichgewichtszuständen gehören und auch auf
unterschiedliche analytische Beziehungen für die spezifische Entropie
führen.
Darüber hinaus konnte gezeigt werden, dass gewisse Anfangsdaten zu
Riemannlösungen führen, die sich nicht mit einer einzigen Art von
Mikrobewegung beschreiben lassen und damit auch nicht auf ein
hyperbolisches System für die Variablen ![]() und T führen.
und T führen.
b) Zuvor hatten wir Mikro-Makro-Übergänge
behandelt, die auf hyperbolische Systeme
und reine Wellenausbreitungsphänomene führen. Im
zweiten Beispiel betrachten wir reine Wärmeleitung für das in [1]
und [2] behandelte kinetische Euler-Schema, wobei die Riemann'schen
Anfangsdaten eine Kontaktunstetigkeit bilden sollen, d. h. die Druckdifferenz
und die Geschwindigkeit ist zu Anfang auf beiden Seiten null. Dadurch ist
sichergestellt, dass auf der großen Zeit-Orts-Skala keine Wellen
entstehen. Die Diffusion entsteht hier aufgrund der Vorgabe einer freien
Flugzeit ![]() der Gasatome und steht im Gegensatz zu dem in
[1], [2] behandelten Euler'schen Grenzfall
der Gasatome und steht im Gegensatz zu dem in
[1], [2] behandelten Euler'schen Grenzfall ![]() ,
der weder Diffusion noch Wärmeleitung beschreiben kann.
,
der weder Diffusion noch Wärmeleitung beschreiben kann.
Wir sehen hier einen endlichen Zeitstreifen der Länge ![]() als mikroskopischen Bereich an und lassen anstelle der Anzahl der Atome N im Falle der Kette die Anzahl n der Zeitschritte mit Länge
als mikroskopischen Bereich an und lassen anstelle der Anzahl der Atome N im Falle der Kette die Anzahl n der Zeitschritte mit Länge ![]() gegen
gegen ![]() gehen. Wählt man dann einen Skalenparameter
gehen. Wählt man dann einen Skalenparameter ![]() proportional zu
proportional zu ![]() , so erhält man eine asymptotische
Grenzlösung, die invariant bzgl. der folgenden Skalentransformation ist:
, so erhält man eine asymptotische
Grenzlösung, die invariant bzgl. der folgenden Skalentransformation ist:
| |
(5) |
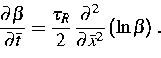 |
(6) |
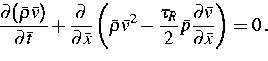 |
(7) |
Wir schließen, dass das Euler-Schema mit ![]() auch
die Lösung für ein gekoppeltes System vom Typ Navier-Stokes-Fourier
liefert.
auch
die Lösung für ein gekoppeltes System vom Typ Navier-Stokes-Fourier
liefert.
Projektliteratur:
|
|
|
[Contents] | [Index] |