|
|
|
[Contents] | [Index] |
Kooperation: S. Orszag (Yale University, USA), T. Vesala (Universität Helsinki, Finnland), P. K. Yeung (Georgian Institute of Technology, USA), O. Kurbanmuradov (Physikalisch-Technisches Institut, Turkmenische Akademie der Wissenschaften, Aschchabad), I. A. Shalimova (Institute of Computational Mathematics and Mathematical Geophysics, Russische Akademie der Wissenschaften, Novosibirsk, Russland), G&W INSTRUMENTS (Berlin), Y. Kashtanov (Universität St. Petersburg, Russland)
Förderung: BMBF, INTAS, NATO
Beschreibung der Forschungsarbeit: Dieses Projekt untersucht die Grundlagen der Modellierung und Numerik von komplexen physikalischen Phänomenen. Komplexe physikalische Zusammenhänge können oftmals durch stochastische Modelle so gut beschrieben werden, dass quantitative Voraussagen über deren Verhalten gemacht werden können. Typische Anwendungen hierfür sind Phänomene der Ausbreitung von Substanzen, Aerosolen in stark fluktuierenden physikalischen Feldern, aber auch der Wellenausbreitung in Medien mit vielen Streuzentren. Das Studium derartiger Modelle ist algorithmisch orientiert. Um in konkreten Anwendungen quantitative Vorhersagen machen zu können, ist eine effiziente, fundierte Numerik unerlässlich. Die numerischen Forschungen im Projekt konzentrieren sich sowohl auf Modelle des Transports von Substanzen und Aerosolpartikeln in turbulenten Medien, wie der Grenzschicht der Atmosphäre, als auch auf hochdimensionale Integrationsprobleme, bei denen eine direkte Simulation der zufälligen Einflüsse nicht möglich ist und nur asymptotisch erwartungstreue Schätzungen verfügbar sind (Markov Chain, Monte Carlo).
Stochastische Modelle für den Transport von Aerosolpartikeln in der Grenzschicht der turbulenten Atmosphäre (Bearbeiter: K. K. Sabelfeld).
Die Menschheit ist mit einer zunehmenden Anzahl von lokalen, regionalen und globalen Umweltproblemen konfrontiert, die mit erheblichen ökologischen, ökonomischen und sozialen Auswirkungen verbunden sind. Die Entwicklung dieser Umweltprobleme wird durch Wechselbeziehungen, Abhängigkeiten und Rückkopplungen geprägt, die ihrerseits die Wirkungskette zwischen Ursache und Folgen der einzelnen Umweltprobleme extrem komplex gestalten. Jede Inhomogenität im Gas kann zur Differenz von Geschwindigkeiten der Partikel führen. Das heißt die relative Geschwindigkeit zwischen zwei Partikeln ist positiv, es ergibt sich eine Kollision und danach eine Koagulation. Wir erwähnen folgende Phänomene, die zur Koagulation führen: Braun'sche Bewegung, Gravitationsfall, freie molekulare Kollision, turbulente Bewegung der tragenden Strömung, akkustische Wellen, die Gradienten der Dichte der Konzentration und der Temperatur, die elektrische Ladung. Folgende Schwerpunkte sind von besonderem Interesse in diesem Projekt:
Als aussichtsreiches Anwendungsgebiet, für das die entwickelten stochastischen Algorithmen und insbesondere die ,,Inverse Trajectory``-Technik effektiv sein sollten, wird das so genannte ,,Footprint-Problem`` ([2], [7]) betrachtet. Dieses Problem kann so formuliert werden: Es ist nötig, den relativen Beitrag verschiedener Quellen der Aerosol-Partikel in einem fixierten Punkt zu berechnen. Dabei wird angenommen, dass die Quellen groß genug sind. (z. B. Auspuffgase). In diesem Fall simuliert man die Trajektorien rückwärts: Die Trajektorien starten aus dem Detektor und enden in den Quellen. Gegenstand des Projekts ist die Konstruktion und Entwicklung neuer stochastischer Modelle und Monte-Carlo-Methoden für die Modellierung des Transports von Substanzen und Aerosolpartikeln in der Grenzschicht der Atmosphäre mit Anwendungen bei der Aufforstung.
Die Aerosol-Partikel wachsen aus dem Gas in einem komplizierten Phasenübergang. Das erste Stadium, die Nukleation, wird mit zwei Hauptmethoden beschrieben; die erste ist die klassische thermodynamische Methode, die die kritische Größe der stabilen Monomeren liefert. Leider kann man mit dieser Methode nur einfachste Systeme behandeln. In der zweiten Methode benutzt man die Smoluchowski-Gleichung mit entsprechenden Verdampfungs- und Kondensations-Koeffizienten.
In beiden Verfahren verwendet man Monte-Carlo-Methoden. Das zweite Stadium ist die Koagulation: Die stabilen Monomeren wachsen über die Kondensation und Kollisionen mit anderen Partikeln. Die Zahl der Gleichungen im Smoluchowski-System ist enorm. Tatsächlich besteht ein Partikel von der Größe eines Mikrons aus etwa 109 - 1010 Atomen, und es ist praktisch nicht möglich, diese Information zu speichern (was aber bei deterministischen Methoden notwendig ist). Die stochastische Beschreibung hat hier den Vorteil, nicht alle Partikel zu behandeln und zu speichern. Ein wichtiges Problem stellt die Abschätzung der Konvergenzgeschwindigkeit des stochastischen Systems, das aus N Partikeln besteht, dar.
Die Geschwindigkeitskomponenten
![]() , in turbulenten Strömungen
werden in der statistischen Strömungsmechanik als
zufällige Felder angesehen. Deshalb sind die Substanzkonzentrationen
auch stochastische Felder. In Anwendungen ist man nicht an
Realisierungen dieser Felder, sondern
an Mittelwerten von Konzentrationen und ihren Flüssen interessiert.
Man verwendet zwei grundlegende Methoden für die
Berechnung dieser Mittelwerte:
, in turbulenten Strömungen
werden in der statistischen Strömungsmechanik als
zufällige Felder angesehen. Deshalb sind die Substanzkonzentrationen
auch stochastische Felder. In Anwendungen ist man nicht an
Realisierungen dieser Felder, sondern
an Mittelwerten von Konzentrationen und ihren Flüssen interessiert.
Man verwendet zwei grundlegende Methoden für die
Berechnung dieser Mittelwerte:
Die Lagrange'schen stochastischen Simulationsmethoden sind frei von der oben erwähnten Einschränkung, und das Verschluss-Problem taucht hier nicht auf. Das Hauptproblem besteht in der Berechnung der Lagrange'schen Übergangsdichte
![]()
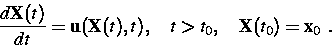
Kennt man die Dichte ![]() ,so kann man die Mittelwerte von Konzentrationen und ihren Flüssen berechnen.
Die Konzentration ist durch folgendes Integral gekennzeichnet ([7]):
,so kann man die Mittelwerte von Konzentrationen und ihren Flüssen berechnen.
Die Konzentration ist durch folgendes Integral gekennzeichnet ([7]):
wobei ![]() die Quelleverteilung ist.
die Quelleverteilung ist.
Die wichtigste Frage ist daher: Wie kann man
die Lagrange'sche Dichte ![]() bei
stochastischen Verfahren konstruieren?
Es gibt zwei grundlegende Methoden im Rahmen der stochastischen
Beschreibung.
bei
stochastischen Verfahren konstruieren?
Es gibt zwei grundlegende Methoden im Rahmen der stochastischen
Beschreibung.
Die erste, die Euler'sche, basiert auf der Simulation der Euler'schen Geschwindigkeit mit gegebener Verteilung; man modelliert die Bewegung der Partikel-Trajektorien mit Hilfe zufällig generierter Geschwindigkeits-Samples. Im Lagrange'schen Schema simuliert man die Lagrange'schen Trajektorien wie einen stochastischen Prozess ([5]) (betrachtet als eine Lösung eines Systems stochastischer Differentialgleichungen).
In Euler'schen Methoden ist es im Prinzip möglich, die Geschwindigkeit bei der DNS-Methode (Direct Numerical Simulation Method) zu simulieren. Die Pionierarbeiten von S. Orszag, der die DNS-Methode vorschlug, behandelten Navier-Stokes-Gleichungen. Leider ist diese Methode nicht anwendbar, wenn die Reynolds-Zahl sehr groß ist. Das bedeutet, man kann die völlig entwickelte Turbulenz nicht mit DNS (wie auch nicht mit anderen numerischen Methoden) simulieren. Deshalb ist die stochastische Behandlung der völlig entwickelten Turbulenz sehr wichtig. Die stochastische Theorie der Turbulenz wurde wesentlich von Taylor, Richardson, Kolmogorov und Obukhov entwickelt.
Die stochastische Simulation des turbulenten Transports, die auf der Randomized-Spektral-Darstellung der Euler'schen turbulenten Geschwindigkeit basiert, wurde zuerst von R. Kraichnan betrachtet. Dieses Modell wurde von weiteren Autoren entwickelt, ausgerichtet und verallgemeinert, in [13] wurde eine weitere Methode, die so genannte ,,Backward Trajectory Technique`` eingeführt. Diese Methode ermöglicht es, die Konzentration des Schadstoffes und die Lagrange'sche Korrelationsfunktion effektiv zu berechnen. Leider ist diese Methode, die auf Monte-Carlo-Simulation der Euler'schen Geschwindigkeit basiert, nur anwendbar, wenn die Geschwindigkeitsfelder homogen und gaußverteilt sind.
In praktischen Anwendungen, z. B. auf Schichten der Atmosphäre, sind die Geschwindigkeitsfelder im Wesentlichen inhomogen, deshalb sind Lagrange'sche Stochastische Modelle (LSM) entwickelt worden, die inhomogene wie auch nichtgaußsche Geschwindigkeitsverteilungen berücksichtigen.
Wir beschreiben nun die wichtigsten Prinzipien, auf denen
die LSM-Methode basiert.
In der LSM-Beschreibung wird die wahre Trajektorie ![]() durch eine simulierte Trajektorie
durch eine simulierte Trajektorie ![]() approximiert, die wie eine Lösung einer
stochastischen Differentialgleichung des Ito-Typs
konstruiert ist (siehe z. B. [6], [10], [15]):
approximiert, die wie eine Lösung einer
stochastischen Differentialgleichung des Ito-Typs
konstruiert ist (siehe z. B. [6], [10], [15]):
wobei mit ![]() die Komponenten der
simulierten Lagrange'schen Geschwindigkeit und mit
B1(t), B2(t),B3(t) die unabhängigen
Standard-Wiener-Prozesse bezeichnet sind; ai und bij
sind im Allgemeinen Funktionen von
die Komponenten der
simulierten Lagrange'schen Geschwindigkeit und mit
B1(t), B2(t),B3(t) die unabhängigen
Standard-Wiener-Prozesse bezeichnet sind; ai und bij
sind im Allgemeinen Funktionen von
![]() . Wir benutzen hier die Summen-Konvention.
. Wir benutzen hier die Summen-Konvention.
Im idealen Fall wünscht man, dass wahre und simulierte Trajektorien
identisch sind:
![]() .Die Konstruktion derartiger Modelle ist nicht realistisch.
Daher benutzt man die folgenden wichtigen Prinzipien. Das
Consistency Principle erfordert, dass die Statistik
simulierter Trajektorien
.Die Konstruktion derartiger Modelle ist nicht realistisch.
Daher benutzt man die folgenden wichtigen Prinzipien. Das
Consistency Principle erfordert, dass die Statistik
simulierter Trajektorien
![]() und wahrer Trajektorien
und wahrer Trajektorien
![]() die gleichen Eigenschaften hat.
Die Lagrange'schen Geschwindigkeitskomponenten sind wie
die gleichen Eigenschaften hat.
Die Lagrange'schen Geschwindigkeitskomponenten sind wie
![]() definiert.
definiert.
Nach der Kolmogorov'schen Analogie-Theorie gilt
![]() wobei wir folgende Bezeichnungen benutzen:
dVi für die Wachstumskomponente der Lagrange'schen Geschwindigkeit,
wobei wir folgende Bezeichnungen benutzen:
dVi für die Wachstumskomponente der Lagrange'schen Geschwindigkeit,
![]() ist die Mittelrate der Dissipation der
Turbulenzenergie, C0 ist eine universelle Konstante
([8]) und
ist die Mittelrate der Dissipation der
Turbulenzenergie, C0 ist eine universelle Konstante
([8]) und ![]() ist das Kronecker'sche Symbol.
Durch
ist das Kronecker'sche Symbol.
Durch ![]() bezeichnet man den
Erwartungswert.
Es heißt, dass (z. B. siehe [15])
in (2) die Koeffizienten bij durch
bezeichnet man den
Erwartungswert.
Es heißt, dass (z. B. siehe [15])
in (2) die Koeffizienten bij durch
![]() definiert sind.
definiert sind.
Die ,,well-mixed condition`` ist in der folgenden Form gegeben ([15]):
Die Funktion ![]() ist die Wahrscheinlichkeitsdichte
der Euler'schen Geschwindigkeit im Punkt
ist die Wahrscheinlichkeitsdichte
der Euler'schen Geschwindigkeit im Punkt ![]() zur Zeit t.
Es wird vorausgesetzt, dass diese Funktion gegeben ist.
In der Praxis nimmt man häufig an, dass sie gaußverteilt ist.
Die Gleichung (3) ist ein System für die
unbekannte Vektorfunktion
zur Zeit t.
Es wird vorausgesetzt, dass diese Funktion gegeben ist.
In der Praxis nimmt man häufig an, dass sie gaußverteilt ist.
Die Gleichung (3) ist ein System für die
unbekannte Vektorfunktion ![]() ,die die
Driftglieder
,die die
Driftglieder ![]() nicht eindeutig definiert.
Tatsächlich können wir eine ganze Reihe von Lösungen
durch Addieren von
nicht eindeutig definiert.
Tatsächlich können wir eine ganze Reihe von Lösungen
durch Addieren von ![]() zu einer beliebigen Vektorfunktion, deren Divergenz
im Geschwindigkeitsraum null ist ([9]),
bekommen.
Es ist bekannt, dass die
,,well-mixed``-Bedingung nur in der Dimension eins
das LS-Modell eindeutig definiert ([15]).
Im mehrdimensionalen Raum besteht folgendes Problem, das
Eindeutigkeitsproblem genannt wird:
Gesucht sind zusätzliche mathematische
Bedingungen, die auch physikalische Bedeutungen haben,
und zusammen mit der ,,well-mixed``-Bedingung eindeutig
die Funktionen
zu einer beliebigen Vektorfunktion, deren Divergenz
im Geschwindigkeitsraum null ist ([9]),
bekommen.
Es ist bekannt, dass die
,,well-mixed``-Bedingung nur in der Dimension eins
das LS-Modell eindeutig definiert ([15]).
Im mehrdimensionalen Raum besteht folgendes Problem, das
Eindeutigkeitsproblem genannt wird:
Gesucht sind zusätzliche mathematische
Bedingungen, die auch physikalische Bedeutungen haben,
und zusammen mit der ,,well-mixed``-Bedingung eindeutig
die Funktionen ![]() bestimmen. Das heißt:
Gesucht werden die
Beschleunigungs-Koeffizienten au, av, aw, die das
LS-Modell eindeutig durch (3) definieren.
bestimmen. Das heißt:
Gesucht werden die
Beschleunigungs-Koeffizienten au, av, aw, die das
LS-Modell eindeutig durch (3) definieren.
Wir haben in [6] das Eindeutigkeitsproblem gelöst und haben ein neues LS-Modell (KS-Modell) vorgeschlagen, das mit dem Thomson-Modell und den experimentellen Messungen gut übereinstimmt. Ausführliche Vergleiche mit anderen Modellen und experimentelle Messungen sind in Tabelle 1 dargestellt.
Model C0 a b c Pr Thomson [15] 3. 0.85 0.65 0.25 0.47 4. 0.71 0.54 0.22 0.6 5. 0.61 0.46 0.2 0.74 7. 0.48 0.35 0.16 1. Flesch & Wilson [2] 3. 0.85 0.65 0.26 0.45 5. 0.61 0.46 0.2 0.8 7. 0.48 0.35 0.16 0.9 KS [6] 3. 0.73 0.55 0.17 0.64 4. 0.59 0.44 0.15 0.82 5. 0.5 0.36 0.14 1. 7. 0.37 0.27 0.11 1.43 Reynolds [11] 3. 0.13 0.09 0.04 5.26 5. 0.18 0.13 0.06 3.3 7. 0.21 0.15 0.07 2.86 MEASUREMENTS
Garger & Zhukov [3] 0.58 0.44 0.19
Chandhry & Meroney [1] 0.4
Rider [12] 0.83
Gurvich [4] 1.25
Simulation der Ultraschallausbreitung (Bearbeiter: P. Mathé, W. Metzner, J.-H. Zacharias-Langhans).
Im Rahmen dieses BMBF-Projekts wurde untersucht, inwieweit sich Techniken aus der Laser-Tomografie auf Ultraschall-Untersuchungen übertragen lassen. Während herkömmliche Ultraschallverfahren lediglich reflektierende Grenzflächen auflösen können, soll das alternative Verfahren zu einer Charakterisierung des von der Schallwelle durchlaufenen Mediums führen. Unmittelbare Anwendungsmöglichkeiten bieten sich in der Medizin, z. B. bei der Krebsdiagnose, sowie in der Materialprüfung, z. B. bei Asbest-Sanierungen. Zwei verschiedene mathematische Modelle, die Telegrafengleichung und die Strahlungstransportgleichung, wurden untersucht, inwieweit sie einerseits die Pulsverformungen bei der Schallausbreitung richtig beschreiben und andererseits die vom Laser her bekannten Eigenschaften aufweisen.
Die bei den von R. Willenbrock und W. Metzner durchgeführten Messungen beobachteten deutlichen Signaldeformationen lassen sich weder durch die Telegraphengleichung noch durch die Randbedingungen, siehe [17], bei Materialübergängen erklären. Dies haben Simulationen, basierend auf der TLM-Methode, gezeigt. Vielmehr werden die Signalveränderungen vom Messgerät selbst und der Geometrie des Versuchsaufbaus bestimmt. Durch Einbeziehung einer (hypothetischen) Gerätefunktion in die Simulation und durch Vergleichsmessungen in Wasser wurde dies bestätigt.
Andererseits haben numerische Experimente mit zufälligen aber frequenzbandbeschränkten Dichte- bzw. Geschwindigkeitsprofilen gezeigt, dass die Signale charakteristische Deformationen erfahren können, zum Beispiel Pulsverbreiterung und Coda-Ausbildung. Wir sind der Ansicht, dass in diesem Bereich die gesuchte Analogie zur Lasertomografie gezogen werden kann. Um dies zu bestätigen, müssen erheblich aufwendigere Messungen durchgeführt werden. Die technischen Voraussetzungen hierzu wurden von der Firma G&W-Instruments erst teilweise geschaffen.
Die mathematischen Untersuchungen zur Lösung der Telegraphengleichung mit Monte-Carlo-Methoden ([16, 18]) führten zur Analyse von stochastischen Prozessen auf Lie-Gruppen, die auf bestimmte Weise durch einen Poissonprozess gestört werden ([19]). Die dem gestörten Prozess entsprechende Differentialgleichung ist im Spezialfall die bereits früher untersuchte Strahlungstransportgleichung. Neben einer Entwicklung nach Potenzen des Störparameters ergibt sich durch diesen Zugang die Möglichkeit zur Analyse der Gleichung mit fourieranalytischen Methoden.
Dynamische Monte-Carlo-Verfahren (Bearbeiter: K. K. Sabelfeld, P. Mathé, J.-H. Zacharias-Langhans).
Viele physikalisch relevante Größen sind entweder Mittelwerte
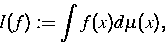
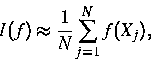
Eng verwandt mit Markov-Chain-Monte-Carlo-Verfahren ist Latin Hypercube Sampling, ein Monte-Carlo-Integrationsverfahren, siehe [24], [27], das im Hochdimensionalen durch gleichzeitige Stratifikation aller Richtungen die Varianz reduziert. Dies kann nur durch eine den Markovketten verwandte innere Abhängigkeit der Stichprobe erreicht werden. Eine detaillierte Analyse der numerischen Eigenschaften ([23]) ergab jedoch, dass die geringere asymptotische Varianz eng mit jedem einzelnen Integranden verknüpft, gleichmäßig auf Klassen nicht nachweisbar ist. Bei zusätzlichen Glattheitsannahmen (H1[0,1]d) kann die Gleichmäßigkeit jedoch erzwungen werden. Diese Untersuchungen ergänzen die bisherige, vorwiegend statistisch orientierte Forschung um numerische Aspekte.
Projektliteratur:
|
|
|
[Contents] | [Index] |