Focus platform: Quantitative Analysis of Stochastic and Rough Systems

We are part of the Research Group Stochastic Algorithms and Nonparametric Statistics of the WIAS.

Members

Christian Bayer (PI)
Simon Breneis
Oleg Butkovsky
Peter K. Friz (PI)
Nikolas E. Tapia M.

Associated members

Paul Hager (Tu Berlin)
John Schoenmakers

Former members

Background

Stochastics plays an increasingly central role in numerous scientific as well as engineering problems, both as a powerful computational tool - multi-level Monte Carlo methods, stochastic gradient descent, expectation maximization (EM) algorithm are just few of many relevant examples - and as a model of uncertainties inherent in complex phenomena.

The aim of this group is to conduct research at the intersection and forefront of the afore-mentioned fields.

Many application areas have recently seen the need to go beyond the paradigm of Markovian stochastic processes - itself a consequence of (over)simplified models based on aggregation of independent random shocks over time. In some fields, that noise exhibits negative auto-correlations, leading to inherent roughness in corresponding stochastic models. That is, continuous time versions of such models area typically rougher than Brownian motion, i.e., α-Hölder continuous with α less than one half. (The prototypical example for such processes is fractional Brownian motion.)

Standard theory of stochastic analysis is poorly equipped to handle such rough noise. However, Terry Lyons' rough path theory provides a methodology for the analysis and numerical treatment of non-Markovian, non-martingale based stochastic systems. After years of foundational work, the last few years have seen multiple breakthroughs, especially in the field of stochastic partial differential equations. These equations are tied to important applications such as stability of non-linear filtering problems or surface growth modelling. Numerical and algorithmic aspects of resulting classes of rough partial differential equations is one of the goals of DFG research unit FOR 2402 / project P3 (PI: Christian Bayer, John Schoenmakers) situated at WIAS.

A key application of rough and stochastic methods is stochastic optimal control in energy and financial markets. As many realistic models of prices in such Markets fail to satisfy the Markov property, we need to use methods of rough stochastic analysis for the theoretical study of such models, as well as for the development of efficient numerical algorithms. Within the Berlin Mathematics Research Center MATH+, we study such problems in the project AA4-2 (PIs: Christian Bayer, Peter Friz, John Schoenmakers, Vladimir Spokoiny).

Of course, rough path and related methods are only one toolsets useful for a proper analysis, control and uncertainty quantification (UQ) of large, complex systems. Future modeling is very likely to be data-driven, hence new methods of data-science (machine learning, deep learning, ...) are crucial. (In his 2014 ICM lecture, Terry Lyons points out several relations to rough paths and signatures; already used for an award-winning Chinese character recognition algorithm.) In addition to afore-mentioned classical inference methods, much emphasis will be given to develop these new ideas, in and beyond the mentioned applications fields. Within the Berlin Mathematics Research Center MATH+, we study such problems in the project EF1-5 (PIs: Christian Bayer, Peter Friz).

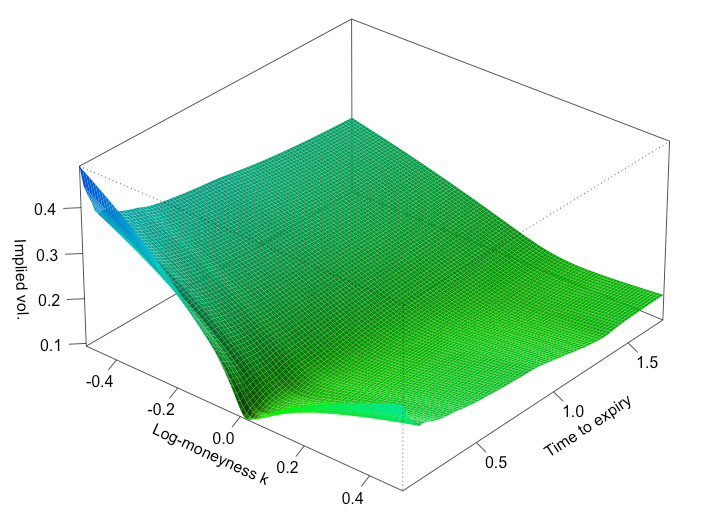
Examples

Regression based methods for random and rough PDEs

Rough volatility models in finance

Funding

We are grateful for the funding provided by:

References