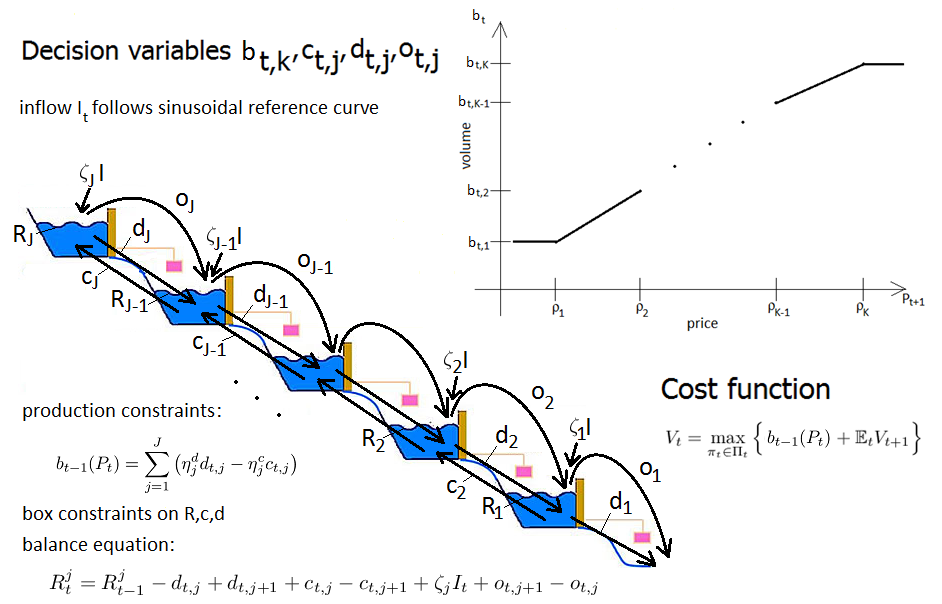
The last decades have seen an expanding competition and complexity in the emerging energy markets, mainly due to the increasing deregulation and privatization of these markets. As a consequence, the dynamics of energy prices have become highly volatile and so energy traders are calling for new instruments and techniques in order to protect their exposures against the risks entailed by the energy markets. A key issue in the energy markets is the fact that energy (in particular oil and gas) can be stored physically. Such storage facilities allow for anticipating and exploiting market fluctuations of energy prices according to the principle “sell high” and “buy low”. Initially, storage facilities were only accessible by major players in the respective industries, who had sufficient capital to build and maintain them. Meanwhile, due to the emerging liberalization of the energy markets all participants have the possibility to trade storage services via storage exchange platforms. As a consequence on the one hand, design of optimal strategies involving buying, storing, and selling energy over time are called for. On the other hand, this resulted in a high demand of proper statistical prediction algorithms based on adequate statistical modeling of energy prices and storage markets. This whole development has further led to the appearance of structured contracts, also called energy derivatives. In the gas and energy markets for example, so called “swing options” have become very popular. An example swing option gives the holder the right to buy or sell a certain amount of gas, electricity or storage capacity at a certain prescribed number of trading dates. Energy derivatives are typically difficult to treat from a quantitative point of view due to their complex structured exercise features and their highly path-dependent structure. As a general consequence, the rising complexity of the markets poses a bunch of challenging mathematical issues that are to be resolved. These issues may be categorized into the following main streams:

• New numerical methods and algorithms for solving multidimensional problems in optimal (multiple) stopping and optimal control
• Adequate modeling of various energy price processes including modern statistical forecast techniques

Particularly in electricity markets, the evaluation of (swing) options requires efficient algorithms for multiple stopping and more complicated control optimization problems. Initially, the dual martingale approach was extended to general optimal control problems by [BSS10]. A first breakthrough was achieved in [Sch12] where a new dual martingale representation for multiple stopping problems was developed. This representation has been extended to much more general pay-off profiles in [BSZ15] (see also [BMS13]). In this extended setting it is possible to treat more realistic energy derivatives by the Monte Carlo method. Such derivatives may involve several volume and exercise refraction constraints, as well as processes driving several underlying energy titles. A novel simulation based primal approach for (standard) multiple stopping, hence the pricing of (simply structured) swing options was developed in [BS06]. A main general goal is the highly non-trivial extension of the above mentioned methods to problems of general control optimization.

We consider problems of optimal control of stochastic processes. Specifically, models of energy storage and production systems coupled with models of energy trading platforms and energy derivatives are considered.
We explore a novel solution method, namely that of penalized dual martingales. This method solves the dual problem, which is posed as finding a martingale acting as Lagrange multiplier of the non-anticipativity constraint of the primal control problem. Any feasible solution of the dual problem yields an upper bound on the objective value of the primal (maximization) problem. The infinite-dimensional dual problem is condensed into a finite-dimensional problem by restricting the set of martingales to a finite-dimensional subspace and solved by Monte-Carlo simulations. In order for the method to converge to an almost surely optimal martingale, i.e., for which the upper bound of the objective value has vanishing variance (see [SZH13]), a penalty term is added to the objective function.
As a first step, a theory of convex penalizations for the dual martingale approach has been developed on the simpler example of an optimal stopping problem, and its convergence properties have been explored (see [BHS15]). As a next step, a more complicated model of a system of coupled water reservoirs for electricity production is being considered. This model is coupled to a model of electricity prices on the spot market, involving day-ahead bids of the energy producers (see [LWM13]). For this model, a dual martingale approach is being developed which is elaborated enough to yield good upper bounds on the objective value yet simple enough to be solvable by the envisaged Monte-Carlo simulations.
In this project we consider a combined model of a hydro-electric storage and production facility and of the day-by-day electricity bid market, involving day-ahead bids of the energy producers. This coupled model has been introduced in [LWM13]. The production facility consists of a number of interconnected water reservoirs. Electricity can be produced from these reservoirs by releasing water from a reservoir situated at higher elevation to one at lower elevation. It can also be stored in the form of potential energy by pumping water from a reservoir at lower elevation to one at higher elevation. The energy conversion efficiency of these processes is lower than 100%, however, and running the water in a cycle leads to a certain loss. The reservoirs are filled by rain and other natural processes, which are modeled as a stochastic process. This process is also coupled to the stochastic process modeling the electricity price. When exploiting the reservoirs, the operator has to meet certain constraints such as not exceeding the capacity of each turbine and not emptying a reservoir completely. Currently the reservoirs are assumed to be ordered linearly, as depicted in the figure below.

A cooperation has been started with the project A-CH3 "Multiview geometry for ophthalmic surgery simulation". This project aims at identifying the location of 3D objects from image data of multiple cameras in real time. Specific semi-definite programming techniques have been discussed to reduce the influence of noise on the reconstruction of the object locations from measurement data.

The project A-CH4 of M. von Kleist, C. Hartmann and M. Weber is concerned with optimal control of a stochastic dynamical system governed by a chemical master equation, which is modeling the evolution of microbial strains which are resistant to different drugs. The dual martingale methods recently developed in [HSZ16] for the optimal control of hydroelectric storage and production systems are to be adapted to the dynamical systems treated in the project A-CH4.

The cooperation with project C-SE13 of M. Eigel, R. Henrion, D. Hoemberg, and R. Schneider has been initiated, consultations on the application of robust stochastic optimization methods to chance-constrained problems are under way.