C-SE13: Topology optimization of wind turbines under uncertainties
| Project heads | Martin Eigel, Dietmar Hömberg, Rene Henrion and Reinhold Schneider |
| Staff | Johannes Neumann, Thomas Petzold |
| Internal Cooperation |
D-OT1 (Hintermüller, Mielke, Surowiec, Thomas) C-SE4 (Kraus, Kutyniok, Wagner) C-SE7 (Schoenmakers, Spokoiny) D-SE9 (Schneider, Tröltzsch) D-SE10 (Schneider) |
| External Cooperation |
Ch. Ruprecht, L. Blank (Universität Regensburg) H. Matthies, E. Zander (TU Braunschweig) |
| Industrial Cooperation | TEMBRA GmbH Wind Turbine Development |
Project background
Introduction The application focus of this project is the topology optimization of the main frame of wind turbines which is the central assembly platform at the tower head. It is a crucial component which has to be designed as light as possible but, at the same time, as rigid as necessary. In order to fully exploit the potential optimizations regarding the design, uncertainties regarding the impurities of the material (cast iron) and the forces acting on the structure have to be taken into account.
A main novelty of this project is that it combines a phase field relaxed topology optimization problem not only with uncertain loading and material data but also with chance state constraints. The latter are introduced to avoid non-admissible large stresses in the structure, a critical problem when engineering such structures.
The work in this project considers recent results on stochastic topology optimization with uncertain data. However, our approach differs in either the stochastic discretization approach or the optimization formulation or both and introduces an alternative phase field based optimization and additional constraints based on finite dimensional stochastic optimization.
Topology Optimization The goal in topology optimization is to partition a given domain into regions occupied by either void or material by minimizing a given cost functional \(J_1(\boldsymbol u,\varphi)\) such that the displacement \(\boldsymbol u\) solves a mechanical equilibrium problem. The material distribution is described with the help of a phase field variable \(\varphi\), taking values in \([0,1]\). To avoid homogenized microstructures, a perimeter penalization \(J_2(\varphi)\) is added to the cost functional.
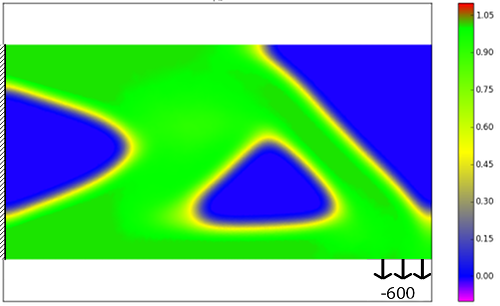

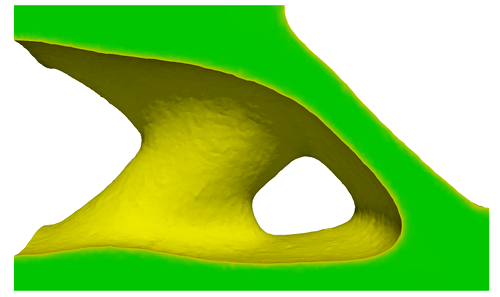

Uncertainty Quantification The incorporation of uncertain parameters in PDE simulations has evolved as one of the most active emerging fields in applied mathematics in recent years. Apart from classical Monte Carlo techniques, methods based on the expansion of stochastic fields in appropriate bases related to a probability space have received great interest in the community. This can be attributed to potentially high convergence rates, possible adaptivity of the expansion and versatility regarding the application areas.
The most popular techniques are stochastic collocation (SC) and stochastic Galerkin FEM (SGFEM). Reliable averaging has only been shown for SGFEM as yet but is also envisaged as part of this project in the context of SC methods. The inclusion of uncertainties comes at the expense of much larger algebraic problems for numerical simulations. Possible remedies for the exponential growth of complexity are model reduction techniques such as hierarchical tensor representations. Such approximations will also be investigated in this project, see [Eigel, Pfeffer & Schneider, 2015] for first results.
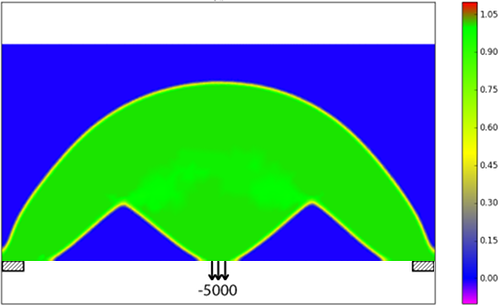
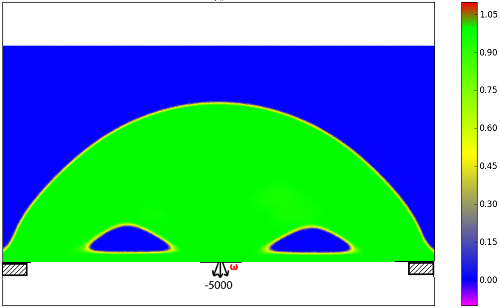
Events
Software
We are developing a software tool for topology optimization of 2D and 3D structures with uncertainties. This is based on the toolbox WIAS-PDELib2 and ALEA.
Publications
Refereed publications
Multi-material Phase Field Approach to Structural Topology Optimization In G. Leugering, P. Benner, S. Engell, A. Griewank, H. Harbrecht, M. Hinze, R. Rannacher, and S. Ulbrich, editors, Trends in PDE Constrained Optimization 165, 231-246, Springer International Publishing 2014
http://dx.doi.org/10.1007/978-3-319-05083-6_15
Relating phase field and sharp interface approaches to structural topology optimization ESAIM: Control, Optimisation and Calculus of Variations 20, 1025-1058, 2014
http://dx.doi.org/10.1051/cocv/2014006
Adaptive stochastic Galerkin FEM Computer Methods in Applied Mechanics and Engineering 270, 247 - 269, 2014
http://dx.doi.org/10.1016/j.cma.2013.11.015
Singular limit of Allen-Cahn equation with constraints and its Lagrange multiplier Dynamical Systems, Differential Equations and Applications, AIMS Proceedings, 418-427, 2015
Tensor spaces and hierarchical tensor representations In Extraction of Quantifiable Information from Complex Systems, 237-261, Springer 2014
Tensor completion in hierarchical tensor representations In H. Boche, R. Calderbank, G. Kutyniok, and Vybiral J., editors, Compressed Sensing and Its Applications 2014
Convergence results for projected line-search methods on varieties of low-rank matrices via Łojasiewicz inequality SIAM J. Optim. 25, 622-646, 2015
http://dx.doi.org/10.1137/140957822
Distortion compensation as a shape optimisation problem for a sharp interface model Computational Optimization and Applications 1-32, 2016
http://dx.doi.org/10.1007/s10589-015-9816-7
Gradient formulae for nonlinear probabilistic constraints with Gaussian and Gaussian-like distributions SIAM Journal on Optimization 24, 1864-1889, 2014
10.1137/130922689
Submitted articles
Iterative Methods Based on Soft Thresholding of Hierarchical Tensors arXiv preprint arXiv:1501.07714v1, accepted in Foundations of Computational Mathematics, 2015
Tensor networks and hierarchical tensors for the solution of high-dimensional partial differential equations accepted in Foundations of Computational Mathematics, 2015
Link: WIAS Preprint 2153
Tensor product methods and entanglement optimization for ab initio quantum chemistry arXiv preprint arXiv:1412.5829, 2014
Theses
Adaptive Methods for the Darcy Equation with Stochastic Input Data PhD thesis, Freie Universität Berlin, 2016
Low Rank Tensor Recovery in the Tensor Train Representation Master’s thesis, Freie Universität Berlin, 2014


