Coupled Schrödinger drift-diffusion models

[Next]:

Stationary energy models for semiconductor devices

[Up]:

Projects

[Previous]:

Supercontinuum generation in nonlinear optical fibers

[Contents]

[Index]

Coupled Schrödinger drift-diffusion models

Collaborator: M. Baro, H.-Chr. Kaiser, H. Neidhardt, J. Rehberg

Cooperation with: N. Ben Abdallah and P. Degond (both Université Paul Sabatier, Laboratoire de Mathématiques pour l'Industrie et la Physique, Toulouse, France), P. Exner (Academy of Sciences of the Czech Republic, Prague), A. Jüngel (Johannes Gutenberg-Universität, Mainz), V.A. Zagrebnov (Centre de Physique Théorique, Marseille, France)

Supported by: DFG Research Center MATHEON (project D4); DFG: ``Spektralparameterabhängige Randwertprobleme und Hybridmodelle der Halbleitersimulation'' (Boundary value problems depending on the spectral parameter and hybrid models in semiconductor simulation); DAAD (PROCOPE): ``Numerics of hybrid models for quantum semiconductors''

Description:

Nowadays, quantum effects play an important role in semiconductor devices. The ongoing progress of industrial semiconductor device technologies permits to fabricate devices which inherently employ quantum phenomena in their operation, e.g., resonant tunneling diodes, quantum well laser, etc. The widely used drift-diffusion equation introduced by van Roosbroeck in 1950 is not capable of properly taking these quantum effects into account. A finer level of modeling has to be used which is achieved by Schrödinger's or equivalently Wigner's equation. However, the numerical treatment of these models is very expensive compared to the drift-diffusion model. In many semiconductor devices, quantum effects take place in a localized region, e.g., around the double barrier in a resonant tunneling diode, whereas the rest of the device is well described by classical models like the drift-diffusion model. Thus, it makes sense to follow a hybrid strategy: Use a quantum model in regions where quantum effects are strong and couple this model by proper interface conditions to a classical model in the rest of the device domain.

In this project we focus on hybrid models, more precisely, coupled Schrödinger drift-diffusion models, which describe the transport within a nanoscaled semiconductor device in a stationary and one-dimensional framework. The semiconductor domain $\Lambda$ = (0, L) is divided into a zone where quantum effects are dominant, called quantum zone $\Omega_{q}^{}$ = (x_l, x_r), and a zone where they can be neglected, the so-called classical zone $\Omega_{c}^{}$ = $\Lambda$ $\setminus$ $\Omega_{q}^{}$ .

On $\Omega_{c}^{}$ we consider a stationary drift-diffusion model, i.e. the current density J and particle density N are determined by the following system of equations
$\begin{subequations} \begin{xalignat}{2} -\frac{d}{dx}J &= 0, && \text{continuit... ...&= F(eV-e\phi-V_h), && \text{particle density,} \end{xalignat}\end{subequations}$
where $\mu$ denotes the mobility of particles, $\phi$ the electrochemical potential, e > 0 is the elementary charge, V the electrostatic potential, V_h the heterostructure potential describing the band-edge offset, and F is the Boltzmann distribution function

F(s) = N₀exp $\displaystyle \left(\vphantom{\frac{s}{k_B T}}\right.$ $\displaystyle {\frac{{s}}{{k_B T}}}$ $\displaystyle \left.\vphantom{\frac{s}{k_B T}}\right)$ ,

with constant lattice temperature T, Boltzmann constant k_B, and density of states N₀.

In the quantum zone $\Omega_{q}^{}$ the particle density n and current density j are given by means of a statistic f and the solutions $\psi$ of Schrödinger's equation, i.e. we regard the following system of equations
$\begin{subequations} \begin{xalignat}{2} \Big(-\frac{\hbar^2}{2}&\frac{d}{dx}\fr... ...\psi_k\vert^2 dE, && \text{particle density,} \end{xalignat}\end{subequations}$
where m = m(x) denotes the effective mass and $\hbar$ the reduced Planck constant. $\psi_{k}^{}$ , k > 0, denote the right-going and $\psi_{k}^{}$ , k < 0, the left-going scattering states, respectively. E(k) is the dispersion relation given by

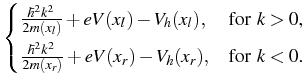
E(k) = $\displaystyle \begin{cases} \frac{\hbar^2k^2}{2m(x_l)}+eV(x_l)-V_h(x_l), & \te... ...\frac{\hbar^2k^2}{2m(x_r)}+eV(x_r)-V_h(x_r), & \text{for $k < 0$.} \end{cases}$

As boundary conditions for the Schrödinger equation we chose either quantum transmitting boundary conditions ([3, 5]) or dissipative-type boundary conditions ([4, 6]).

The drift-diffusion (1) and Schrödinger model (2) are coupled by the following conditions:

The distribution function f in (2) is given by

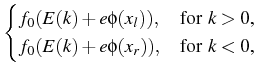
f (k) = $\displaystyle \begin{cases} f_{0}(E(k)+e\phi(x_l)), &\text{for $k>0$,}\\ f_{0}(E(k)+e\phi(x_r)), &\text{for $k<0$,} \end{cases}$
where $\phi$ is the electrochemical potential, f₀ is a reduced equilibrium distribution function of the two-dimensional carrier gas, e.g.,

f₀( $\displaystyle \xi$ ) = n₀exp $\displaystyle \left(\vphantom{\frac{-\xi}{k_B T}}\right.$ $\displaystyle {\frac{{-\xi}}{{k_B T}}}$ $\displaystyle \left.\vphantom{\frac{-\xi}{k_B T}}\right)$ ,
and n₀ denotes the integrated density of states.
We impose the continuity of the current densities, i.e.

J(x_l) = j = J(x_r),
which is a condition for the coupling that is consistent with physics.
In order to have a meaningful description of the semiconductor device, the electrostatic potential V has to be computed self-consistently on the whole device domain $\Lambda$ by Poisson's equation

- $\displaystyle {\frac{{d}}{{dx}}}$ $\displaystyle \epsilon$ $\displaystyle {\frac{{d}}{{dx}}}$ V = e $\displaystyle \Big($ D - $\displaystyle \mathcal {N}$ $\displaystyle \Big)$ , (3)

where $\epsilon$ = $\epsilon$ (x) is the dielectric permittivity function, D the density of ionized dopants in the semiconductor device, and $\mathcal {N}$ is the particle density, i.e.

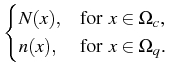
$\displaystyle \mathcal {N}$ (x) = $\displaystyle \begin{cases} N(x), & \text{for $x\in\Omega_c$,}\\ n(x), & \text{for $x\in\Omega_q$.} \end{cases}$

The coupled system is completed by imposing charge neutrality as boundary conditions for (1)

N(0) = D(0), N(L) = D(L),

and the applied bias V_b as boundary conditions for the Poisson equation (3), i.e.

V(0) = 0, V(L) = V_b.

In [2], we show that the coupled system--with dissipative boundary conditions for the Schrödinger equation--is well posed and admits a solution. Moreover, we show that similar results hold for the bipolar system, where electrons and holes have to be considered.

The validity of the model is illustrated in [1], where the model is used to calculate current-voltage characteristics of resonant tunneling diodes. Resonant tunneling diodes are typical examples of devices whose functionality depends on quantum effects and thus cannot be described by the usual drift-diffusion model. We show that the hybrid model presented above is capable to describe the transport of electrons in a resonant tunneling diode and investigate the influence of the position of the quantum zone $\Omega_{q}^{}$ . If the quantum zone is chosen properly, good results are obtained, see Figure 1. Additionally, collisions in the quantum zone have been taken into account by means of a Pauli master equation.

**Fig. 1:** The left figure shows the current-voltage characteristic of the device ([7]) calculated by means of the coupled Schrödinger drift-diffusion model.The calculated transmission coefficient and the potential profile for the current peak bias are depicted on the right figures.
$\makeatletter \@ZweiProjektbilderNocap[h]{.46\linewidth}{jfb04_fg1_bknr-0.eps}{jfb04_fg1_bknr-1.eps} \makeatother$

References:

M. BARO, N. BEN ABDALLAH, P. DEGOND, A. EL AYYADI, A 1D coupled Schrödinger drift-diffusion model including collisions, J. Comput. Phys., 203 (2005), pp. 129-153.
M. BARO, H. NEIDHARDT, J. REHBERG, Current coupling of drift-diffusion models and dissipative Schrödinger-Poisson systems: Dissipative hybrid models, WIAS Preprint no. 946, 2004, to appear in: SIAM J. Math. Anal.
M. BARO, H.-CHR. KAISER, H. NEIDHARDT, J. REHBERG, A quantum transmitting Schrödinger-Poisson system, Rev. Math. Phys., 16(3) (2004), pp. 281-330.
, Dissipative Schrödinger-Poisson systems, J. Math. Phys., 45(1) (2004), pp. 21-42.
N. BEN ABDALLAH, P. DEGOND, P.A. MARKOWICH, On a one-dimensional Schrödinger-Poisson scattering model, Z. Angew. Math. Phys., 48 (1997), pp. 135-155.
H.-CHR. KAISER, H. NEIDHARDT, J. REHBERG, Macroscopic current induced boundary conditions for Schrödinger-type operators, Integral Equations Operator Theory, 45 (2003), pp. 39-63.
P. MOUNAIX, O. VANBESIAN, D. LIPPENS, Effect of space layer on the current-voltage characteristics of resonant tunneling diodes, Appl. Phys. Lett., 57(15) (1990), pp. 1517-1519.