Collaborator: U. Bandelow,
A. Demircan,
M. Kesting
Cooperation with: M. Kroh, H.G. Weber (Fraunhofer-Institut für
Nachrichtentechnik, Heinrich-Hertz-Institut (HHI) Berlin)
Supported by: Terabit Optics Berlin (project B4)
Description:
The propagation of short and intense optical pulses through a nonlinear optical fiber
is described by the nonlinear Schrödinger equation (NLSE).
Our model uses the following form of the NLSE for the complex
envelope A(z,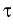 ) of an optical pulse which includes
group velocity dispersion up to fourth order as well as self-steepening and
Raman scattering:
) of an optical pulse which includes
group velocity dispersion up to fourth order as well as self-steepening and
Raman scattering:
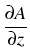 |
= |
- 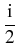 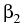 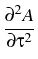 + + 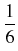 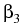 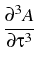 + + 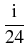 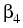 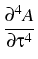 - - 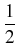 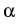 A A |
|
| |
|
+ i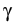 | A|2A - | A|2A - 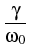 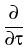 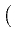 | A|2A | A|2A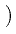 - i - i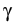 TR A TR A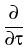 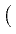 | A|2 | A|2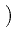 . . |
(1) |
The details of the derivation of this equation are given in [1].
The numerical investigation of Eq. 1
in view of the supercontinuum (SC) generation [3]
requires a high accuracy as well as a high resolution.
We use a de-aliased pseudospectral method with integration performed by an
eighth-order Runge-Kutta integration scheme using adaptive stepsize control
[1,2]
which is more precise than the widely-used split-step method.
Experimental and numerical investigations
[3,4,5]
show the importance of higher-order dispersion terms. It turns out to be highly questionable whether the use of even
higher-order dispersion terms resulting from a Taylor expansion in the
Fourier domain is reasonable.
This led us to a review of the modeling process to come up with more
general equations.
Concerning nonlinear Schrödinger equations, one may start with the
following scheme:
iuz + 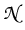 (u) + (u) + 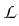 u = 0, u = 0,
|
(2) |
where
u : 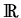 x
x 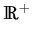
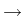
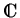 , (
, (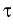 , z)
, z) 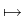 u(
u(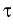 , z).
The linear operator
, z).
The linear operator
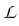 describing the dispersion is determined by the
dispersion relation
describing the dispersion is determined by the
dispersion relation
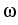 (
(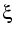 ) in the Fourier domain as follows:
) in the Fourier domain as follows:
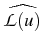 (
(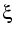 ) =
) = 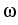 (
(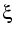 )
)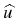 (
(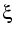 ).
In the case of
).
In the case of 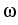 being a polynomial (e.g., from a Taylor expansion),
being a polynomial (e.g., from a Taylor expansion),
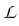 is a differential operator and the equation is therefore local.
Choosing non-polynomial functions for
is a differential operator and the equation is therefore local.
Choosing non-polynomial functions for 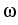 leads to pseudo-differential
operators and nonlocal equations on which we focused our analysis.
Similar to that it is worth to ask for generalizations of the nonlinearity
leads to pseudo-differential
operators and nonlocal equations on which we focused our analysis.
Similar to that it is worth to ask for generalizations of the nonlinearity
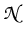 (u).
We have investigated the case
(u).
We have investigated the case
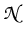 (u)(
(u)(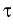 , z) = u(
, z) = u(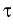 , z)
, z) R(
R(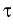 )*| u(
)*| u(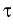 , z)|2
, z)|2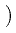 ,
which is suggested by the physical model.
The convolution with R describes the response of the material and we have
R(
,
which is suggested by the physical model.
The convolution with R describes the response of the material and we have
R(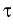 ) =
) = 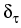 in the standard case where only instantaneous response is
considered (
in the standard case where only instantaneous response is
considered (
 (u) = u| u|2).
(u) = u| u|2).
On the other hand, we validated our algorithm by the substantial example of
supercontinuum generation [4,5],
which apparently comprises all physical effects modeled by Eq. 1.
We demonstrate in [3] that the modulation instability (MI),
which is a special four-wave-mixing process,
can be responsible for
ultrabroadband octave-spanning continua for pico- and subpicosecond pulses
in the anomalous as well as in the normal dispersion region.
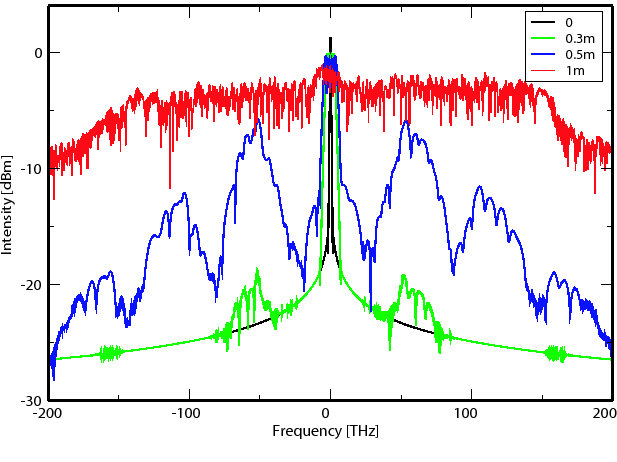
We illustrate the effect of MI in Figure 1.
Fig. 1:
Spectra of an initial sech pulse with
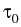 = 1ps with a peak input
power P0 = 400 W and TR = 3 fs at different propagation distances.
The initial spectrum has a sech profile (black). After 0.3 m (green), the MI
generates two sidebands at
= 1ps with a peak input
power P0 = 400 W and TR = 3 fs at different propagation distances.
The initial spectrum has a sech profile (black). After 0.3 m (green), the MI
generates two sidebands at
 50 THz (Stokes and anti-Stokes components),
which are multiplied after 0.5 m (blue).
Further phase-matched four-wave mixing then explosively excites
new frequencies and hence broadens and completes the spectrum afterwards
(red).
50 THz (Stokes and anti-Stokes components),
which are multiplied after 0.5 m (blue).
Further phase-matched four-wave mixing then explosively excites
new frequencies and hence broadens and completes the spectrum afterwards
(red).
 |
The MI can dominate higher-order effects such as
third- and fourth-order dispersion, self-steepening, and Raman scattering,
because it acts directly from the beginning on the high-order solitons.
Therefore higher-order effects are not a prerequisite for the generation of SC,
and it is hence not restricted only to ultrashort subpicosecond pulses,
but appears for much longer pulses, too.
The MI can also appear in the normal dispersion regime 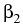 > 0, if the
fourth-order dispersion coefficient
> 0, if the
fourth-order dispersion coefficient 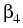 is negative.
In particular, we have verified quantitatively the experimental results in
[4],
where the MI sidebands are observed in the normal dispersion
regime with negative
is negative.
In particular, we have verified quantitatively the experimental results in
[4],
where the MI sidebands are observed in the normal dispersion
regime with negative 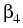 . For these calculations a resolution of 219
frequencies is required.
The calculated wavelenghts of the Stokes (
. For these calculations a resolution of 219
frequencies is required.
The calculated wavelenghts of the Stokes (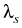 ) and anti-Stokes
(
) and anti-Stokes
(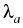 ) components are represented in the following table:
) components are represented in the following table:
| P0 [W] | 100 | 150 | 200 | 250 | 300 | 350 | 400 |
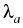 [nm] [nm] | 503.84 | 502.9 | 502.26 | 501.37 | 501.45 | 501.51 | 501.48 |
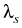 [nm] [nm] | 903.79 | 906.84 | 907.97 | 911.84 | 911.75 | 911.40 | 911.49 |
in dependence on the optical input power P0.
In applications, the effect of spectral broadening of a pulse propagating through
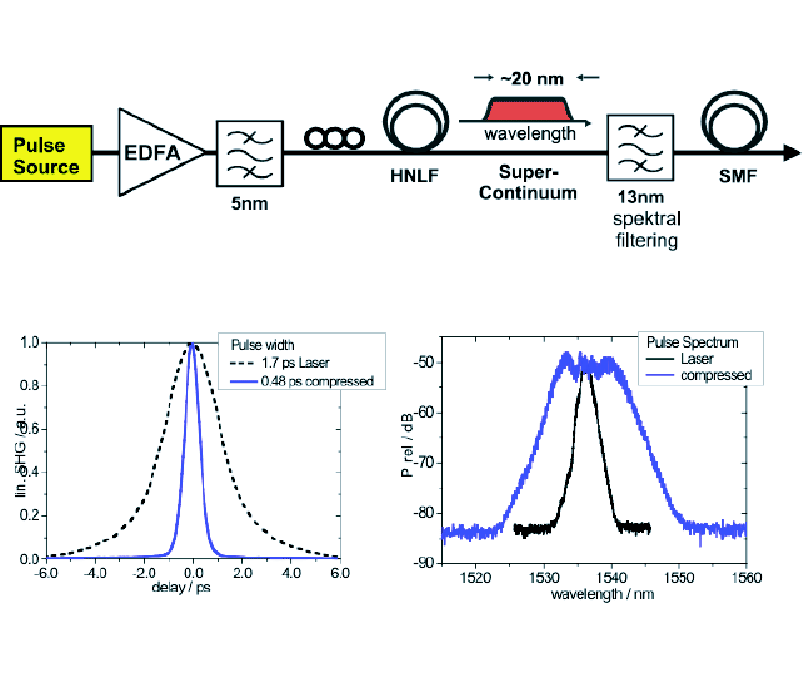
a fiber is used for pulse compression. A schematic of the experimental setup is shown
in Figure 2. A highly nonlinear fiber (HNLF) is used to induce a linear chirp in the spectral broadening process and the chirped pulses are compressed by dispersion compensation in a subsequent standard single mode fiber (SMF).
Applications require flat and wideband spectra without
phase instabilities.
This is achieved by the self-phase modulation
(i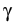 | A|2A) in Eq. 1
as the main broadening mechanism.
The corresponding spectral broadening is confirmed by the measurements.
One example is shown in Figure 3.
| A|2A) in Eq. 1
as the main broadening mechanism.
The corresponding spectral broadening is confirmed by the measurements.
One example is shown in Figure 3.
The experimental investigations at the HHI as well as our numerical
simulations indicate an optimal pulse compressor in the vicinity of
the zero-dispersion wavelength in the normal dispersion regime
leading to a linear up-chirp across the entire pulse width.
Fig. 2:
Upper: Experimental setup used in the HHI for pulse compression using a HNLF.
Lower left: measured pulse shape
(black: before compression, blue: after compression).
Lower right: measured pulse spectrum
(black: before compression, blue: after compression).
We acknowlegde the permission by Prof. Weber and M. Kroh
(HHI) to show these figures.
 |
We have simulated the spectral broadening for realistic fibers and have compared
our results with measurements, results are plotted in Figure 3.
A typical problem for such investigations is
that the fiber coefficients of a realistic fiber are not exactly known.
Therefore, we first used measurements at low optical power
for a proper adjustment of the dispersion coefficients.
The resulting spectrum is drawn in Figure 3, left.
Then we used the simulation parameters obtained in this way for further
simulations with higher optical input power.
For medium input power (20.0 dBm sech input) we again obtained good agreement
with the experiments.
Furthermore, we could reconstruct the measured pulse compression down
to 0.4 ps. We obtained good agreement with the measurements for even higher input power.
Surprisingly, no further pulse compression could be achieved by
increasing the
input power, which is due to the occurrence of other disturbing nonlinearities.
The latter can now be studied with our tools in order to design a proper HNLF.
Fig. 3:
Measured optical spectra
(black, HHI, for a train of identical pulses) and
calculated optical spectra for a single pulse (red, based on Eq. 1)
after propagation over 510 meters along a HNLF;
left: low input power, right: high input power.
![\makeatletter
\@ZweiProjektbilderNocap[h]{0.48\textwidth}{17k5dBm.eps}{21k25dBm}
\makeatother](img47.gif) |
References:
-
U. BANDELOW, A. DEMIRCAN, M. KESTING,
Simulation of pulse propagation in nonlinear optical fibers,
WIAS Report no. 23, 2003
.
- N. SEEHAFER, A. DEMIRCAN,
Dynamo action in cellular pattern,
Magnetohydrodynamics, 39(3) (2003), pp. 335-344.
- A. DEMIRCAN, U. BANDELOW,
Supercontinuum generation by the modulation instability,
Optics Communications, 244(6) (2005), pp. 181-185.
- J.D. HARVEY, R. LEONHARDT, S. COEN, G.K.L. WONG, J.C. KNIGHT,
W.J. WADSWORTH, P.S.J. RUSSEL,
Scalar modulation instability in the normal dispersion regime by use of a photonic crystal fiber,
Optics Letters, 28(22) (2003), pp. 2225-2227.
- W.J. WADSWORTH, N. JOLY, J.C. KNIGHT, T.A. BIRKS, F. BIANCALANA, P.S.J. RUSSEL,
Supercontinuum and four-wave mixing with q-switched pulses in endlessly single-mode photonic crystal fibres,
Optics Express, 12(2) (2004), pp. 299-309.
LaTeX typesetting by H. Pletat
2005-07-29
![]() ) of an optical pulse which includes
group velocity dispersion up to fourth order as well as self-steepening and
Raman scattering:
) of an optical pulse which includes
group velocity dispersion up to fourth order as well as self-steepening and
Raman scattering:

![]() | A|2A) in Eq. 1
as the main broadening mechanism.
The corresponding spectral broadening is confirmed by the measurements.
One example is shown in Figure 3.
| A|2A) in Eq. 1
as the main broadening mechanism.
The corresponding spectral broadening is confirmed by the measurements.
One example is shown in Figure 3.

![\makeatletter
\@ZweiProjektbilderNocap[h]{0.48\textwidth}{17k5dBm.eps}{21k25dBm}
\makeatother](img47.gif)