Subsections
Collaborator: W. Dreyer,
F. Duderstadt,
S. Qamar,
B. Wagner
Cooperation with: W.H. Müller (Technische Universität Berlin), P. Colli, G. Gilardi (Università di Pavia, Italy), S. Eichler, G. Jurisch (Freiberger Compound Materials GmbH), T. Hauck (Motorola, München/Berlin), B. Niethammer (Humboldt-Universität zu Berlin)
Supported by: BMBF: ``Mathematische Modellierung und Simulation der
Entstehung, des Wachstums und der Auflösung von
Arsenausscheidungen
in einkristallinem Galliumarsenid''
(Mathematical modeling and simulation of the formation, growth and
dissolution of arsenic precipitation in single crystal gallium
arsenide)
Description:
A careful study of a sharp interface limit of the existing phase field model,
that was used in the past to describe morphological changes in eutectic
tin/lead alloys, exhibited that anisotropic surface energies can only be
generated due to mechanical effects. This is one of the reasons that the
diffusion flux was reformulated by W. Dreyer and B. Wagner. The resulting
thermodynamically consistent form now reads
| Jk |
= |
 - - 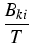 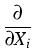 ( (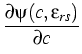 -2Ajl(c, -2Ajl(c,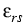 ) )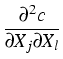 - - 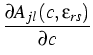   |
|
| |
|
 -2 -2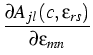 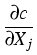 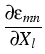 - - 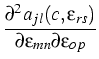 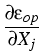 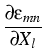 - - 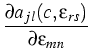 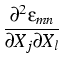 ). ). |
(1) |
The variables are the (tin) concentration c and the strain
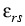 . Bki gives the mobility tensor and T is the temperature. The
functions
. Bki gives the mobility tensor and T is the temperature. The
functions
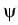 (c,
(c,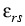 ),
Ajl(c,
),
Ajl(c,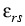 ), and
ajl(c,
), and
ajl(c,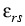 ) are explicitly known, see [3]. In the
sharp interface limit of this model there results a surface tension that can
be calculated from the gradient coefficients
Ajl(c,
) are explicitly known, see [3]. In the
sharp interface limit of this model there results a surface tension that can
be calculated from the gradient coefficients
Ajl(c,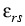 ).
).
In the first numerical treatment of the resulting phase field equation, B.
Wagner ignored the mechanical contributions and developed a non-stiff boundary
integral formulation to efficiently simulate the long-time evolution of
precipitates during coarsening.
The description of semi-insulating GaAs, which includes thermo-mechanical
coupling, diffusion, interface motion, precipitation of arsenic droplets, and
the determination of various thermodynamic equilibria, has been completed. The
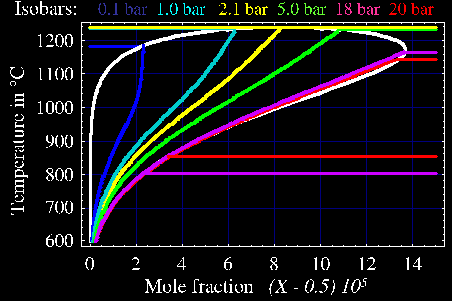
material parameters have been tested and make it possible to calculate the
phase diagram of GaAs, which is in exact agreement with the experimental data.
The Figure shows a region of the phase diagram of GaAs, where the doping
substances are distributed randomly over the three sublattices. Outside this
region, precipitation of arsenic droplets sets in. The upper endpoints of the
isobars are triple points, where solid, liquid, and gas phase are in equilibrium.
For an illustration of the involved field equations in non-equilibrium
processes, we give, as an example, the diffusion equation, which describes the
concentration field y(t, r) of the interstitial arsenic in the vicinity of a
spherical arsenic droplet.
Herein, D denotes the diffusion constant, R and T are the gas constant and
the temperature, respectively, M is the molecular weight of the arsenic, G
denotes the shear modulus, and
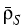 is the mass density of the
solid. The quantity b measures the phenomenon that the liquid droplet needs
more space than a solid of the same number of particles, leading to a
multiaxial stress field in the vicinity of the droplet. Note that b depends
implicitly on time via the evolving radius rI(t) of the droplet. More
details can be found in [4].
is the mass density of the
solid. The quantity b measures the phenomenon that the liquid droplet needs
more space than a solid of the same number of particles, leading to a
multiaxial stress field in the vicinity of the droplet. Note that b depends
implicitly on time via the evolving radius rI(t) of the droplet. More
details can be found in [4].
are due
to the Grinfeld instability, which is a phenomenon of growing interest.
The Grinfeld instability states that a plane interface between a solid and its
melt may become unstable if multiaxial stress fields appear in the solid.
Surface tension and gravity provoke a stabilization of a plane interface. We
found a further phenomenon in the competition of these effects. It is
important whether the creation/annihilation of the melt decreases or increases
the volume that is occupied by the two-phase mixture. This has the consequence
that the stability of a plane interface depends on further conditions, which
are:
(i) Do we consider an infinite system without mass conservation or a
finite system with mass conservation?
(ii) Do we control the total volume or
the total pressure of the considered system?
Our study of the Grinfeld instability relies on the solution of a quasistatic
elastic problem for the stresses in the solid and the pressure in the melt.
Both are used to calculate the interfacial normal speed w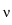 , which is
given by (see [1])
, which is
given by (see [1])
Here MI > 0 denotes the interfacial mobility, 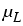 and
and 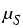 are
chemical potentials of the melt and the solid, respectively,
are
chemical potentials of the melt and the solid, respectively, 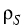 is
the mass density of the solid at the interface,
is
the mass density of the solid at the interface,
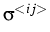 denote the
trace-free components of the stress tensor, and
denote the
trace-free components of the stress tensor, and 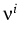 are the components of
the interfacial normal. This equation becomes a nonlinear and nonlocal PDE
determining the geometry of the interface, if the liquid pressure and the
stress fields of the mechanical boundary value problem have been inserted. The
main results can be found in [2].
are the components of
the interfacial normal. This equation becomes a nonlinear and nonlocal PDE
determining the geometry of the interface, if the liquid pressure and the
stress fields of the mechanical boundary value problem have been inserted. The
main results can be found in [2].
References:
- W. DREYER, On jump conditions at phase boundaries for ordered
and disordered phases, WIAS
Preprint no. 869, 2003
.
- W. DREYER, A. MÜNCH, B. WAGNER, On the Grinfeld instability, to appear as WIAS Preprint.
- W. DREYER, B. WAGNER, Sharp-interface model for eutectic alloys. Part I: Concentration dependent surface tension, WIAS
Preprint no. 885, 2003
.
- W. DREYER, F. DUDERSTADT, S. QAMAR, Diffusion in the vicinity of an evolving spherical arsenic
droplet, to appear as WIAS Preprint.
LaTeX typesetting by I. Bremer
2004-08-13
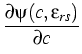 -2Ajl(c,
-2Ajl(c,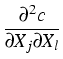 -
- 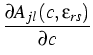
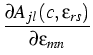
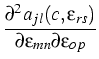
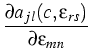
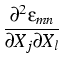 ).
).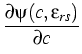 -2Ajl(c,
-2Ajl(c,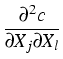 -
- 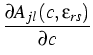
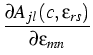
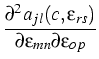
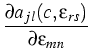
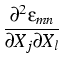 ).
).
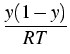
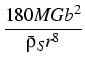 ) -
) - 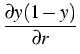
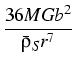 .
.
![]() , which is
given by (see [1])
, which is
given by (see [1])