[Next]:

Research Group Numerical Mathematics and Scientific

[Up]:

Projects

[Previous]:

Dynamics of semiconductor lasers

 [Contents] 

 [Index] 

Subsections

• Project 1: Blue-sky catastrophe in singularly perturbed systems
• Project 2: Exchange of stabilities in multiscale systems
• Project 3: Integral manifolds loosing their attractivity
• Project 4: Maximal temperature of safe combustion in case of an autocatalytic reaction

Multiscale systems

Collaborator: K.R. Schneider, E.V. Shchetinina, D. Turaev (until 10/03)

 

Project 1: Blue-sky catastrophe in singularly perturbed systems

(D. Turaev).

Cooperation with: A.L. Shilnikov (Georgia State University, Atlanta, USA), L.P. Shilnikov (Institute for Applied Mathematics and Cybernetics, Nizhny Novgorod, Russia)

Description:

One of the basic questions of dynamics concerns the structure of the regions of stability of periodic orbits. The last known stability boundary was discovered only in 1995, [1]. It corresponds to the so-called blue-sky catastrophe, a special case of a saddle-node bifurcation where a saddle periodic orbit collides with a stable one, then both disappear, and a single stable periodic orbit with very large length and period is created (the length and period tend to infinity when the bifurcational moment is approached). The global structure of the unstable set of the saddle-node for the blue-sky catastrophe appears to be rather complex. Nevertheless, it was shown in [2] that this particular configuration of the unstable set is, in fact, quite typical for singularly perturbed systems with at least two fast variables.

A singularly perturbed system, a paradigm for dynamical processes with two distinct time scales, is a system of the form

$$\dot{x} \varepsilon$$ =

$$\varepsilon \dot{y} \varepsilon$$ =

where $\varepsilon$ > 0 is a small parameter; x stands for the slow variables and y for the fast ones. The y equation for fixed x is called a fast system. The dynamics of singularly perturbed systems is characterized by the slow motion along the invariant manifolds corresponding to attractors of the fast system (equilibria or periodic orbits in the simplest situation) and by fast jumps between different such manifolds. The jumps happen at the values of x which correspond to bifurcations in the fast system.

In this project we show ([3]) that the blue-sky catastrophe almost inevitably accompanies the saddle-node bifurcation in the slow-fast systems, where there are jumps between invariant manifolds corresponding to fast periodic orbits and those corresponding to fast equilibria. We present and analyze three distinct specific scenarios which lead to the blue-sky catastrophe in the singularly perturbed systems. These scenarios correspond to three different types of jumps, caused either by a saddle-node bifurcation in the fast system, or by an Andronov-Hopf bifurcation, or by a homoclinic loop.

Fig. 1: At $\mu$ < $\mu^{*}_{}$($\varepsilon$) the system has two periodic orbits: a stable orbit L⁺ and a saddle orbit L^-. The orbits which do not lie in the stable manifold of L^- tend to L⁺ as time increases. At $\mu$ > $\mu^{*}_{}$($\varepsilon$) the system has a single and attracting limit cycle L_$\mu$ whose length tends to infinity as $\mu$ $\rightarrow$ $\mu^{*}_{}$($\varepsilon$) + 0.

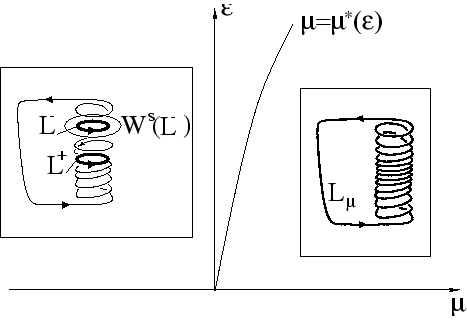We remark that the suggested mechanisms of the blue-sky catastrophe in singularly perturbed systems have indeed been reported in models of neuronal activity, for example, describing the dynamics of the leach heart interneurons ([4]). The transition (illustrated in Fig. 1) from one type of self-sustained oscillations (a round stable periodic orbit L⁺) to the regime where the attractor is the ``long'' stable orbit L_$\mu$ can be interpreted as a transition from periodic tonic spikes to periodic bursting oscillations of the neuron.

Note as well that even before the transition to the bursting oscillations the spiking mode is in an excitable state here: a perturbation which drives the initial point outside the saddle limit cycle L^- results in a long calm phase before the sustained spiking restores.

References:

1. D.V. TURAEV, L.P. SHILNIKOV, Blue sky catastrophes, Dokl. Math., 51 (1995), pp. 404-407.

2. L. SHILNIKOV, A. SHILNIKOV, D. TURAEV, L. CHUA, Methods of Qualitative Theory in Nonlinear Dynamics. Part II, World Scientific, Singapore, 2001.

3. A. SHILNIKOV, L. SHILNIKOV, D. TURAEV, Blue sky catastrophe in singularly-perturbed systems, WIAS Preprint no. 841 , 2003, to appear in: Moscow Math. J.

4. A. SHILNIKOV, G. CYMBALYUK, R. CALABRESE, Multistability and infinite cycles in a model of the leach heart interneuron, Proc. NDES 2003.

Project 2: Exchange of stabilities in multiscale systems

(E.V. Shchetinina, K.R. Schneider).

Cooperation with: V.F. Butuzov, A.B. Vasil'eva, N.N. Nefedov (Moscow State University, Russia)

Supported by: DFG: Cooperation Project ``Singulär gestörte Systeme und Stabilitätswechsel'' (Singularly perturbed systems and exchange of stability) of German and Russian scientists in the framework of the Memorandum of Understanding between DFG and RFFI

Description:

Consider a dynamical system of the type dx/dt = f (x,$\lambda$) and assume that the parameter $\lambda$ slowly changes in time. Setting $\lambda$ $\equiv$ $\varepsilon$$\tau$ we obtain after rescaling t the singularly perturbed non-autonomous differential equation

$$\varepsilon {\frac{{du}}{{dt}}} \varepsilon \ll$$ (1)

We suppose that the solution set f^-1(0) of the degenerate equation of (1)

0 = f (u, t)

consists in the (t, u)-plane of two curves k₁(u $\equiv$ 0) and k₂ intersecting transversally for t = 0. If the solution $\overline{{u}}$(t, u⁰,$\varepsilon$) of (1), satisfying u(t₀) = u⁰ for t₀ < 0, exists for t > 0, then the behavior near t = 0 can be characterized by one of the following cases:

(i)

$\overline{{u}}$(t, u⁰,$\varepsilon$) follows immediately the stable branch of k₂,

(ii)

$\overline{{u}}$(t, u⁰,$\varepsilon$) follows for some O(1)-time interval (not depending on $\varepsilon$) the unstable part of k₁ and then jumps either to the stable part of k₂ or to infinity (blowing up).

The case (i) is called an immediate exchange of stabilities, the case (ii) is referred to as delayed exchange of stabilities or as delayed loss of stability. These cases cannot be treated by applying the standard theory of singularly perturbed systems. In [1], [2], [3], we have developed a theory based on the method of asymptotic upper and lower solutions to characterize and to distinguish immediate and delayed exchange of stabilities. In the project under consideration we study equation (1) under the assumption that the curves k₁ and k₂ intersect in at least two different points. By means of the method of asymptotic upper and lower solutions we derive conditions on f guaranteeing that the solution of the initial value problem exhibits the phenomena of immediate as well as of delayed exchange of stabilities. It is important to emphasize that it is not possible to prove this result by only verifying the assumptions for immediate and delayed exchange of stabilities. In fact, we have to look for an appropriate modification of the method of asymptotic upper and lower solutions. We also study the case that f is periodic in t. In order to be able to prove the existence of a harmonic solution which represents a periodic forced canard we have to construct asymptotic upper and lower solutions which are discontinuous and contain boundary layer functions.

References:

1. N.N. NEFEDOV, K.R. SCHNEIDER, Immediate exchange of stabilities in singularly perturbed systems, Differ. Integral Equ., 12 (1999), pp. 583-599.

2.          , Delayed exchange of stabilities in singularly perturbed systems, Z. Angew. Math. Mech., 78 (1998), pp. S199-S202.

3. V.N. BUTUZOV, N.N. NEFEDOV, K.R. SCHNEIDER, Singularly perturbed problems in case of exchange of stabilities, WIAS Report no. 21 , 2002.

4. N.N. NEFEDOV, K.R. SCHNEIDER, On immediate-delayed exchange of stabilities and periodic forced canards, WIAS Preprint no. 872 , 2003.

Project 3: Integral manifolds loosing their attractivity

(E.V. Shchetinina, K.R. Schneider).

Cooperation with: V.A. Sobolev, E.A. Shchepakina (Samara State University, Russia)

Description:

We consider slow-fast systems that can be transformed into the form

$\parbox{11cm}{ \begin{eqnarray*} \frac{dy}{dt}&=&\varepsilon Y(t,... ...B(t)z+Z(t,y,z,a(y,\varepsilon),\varepsilon)+a(y,\varepsilon), \end{eqnarray*}}$ $\parbox{1cm}{ \begin{eqnarray} \end{eqnarray}}$

where y $\in$ Rⁿ, z $\in$ R², $\varepsilon$ is a small positive parameter, a is a two-dimensional vector function, and B(t) is the matrix

B(t) = $$\left(\vphantom{ \begin{array}{cc} \alpha t&\beta -\beta&\alpha t \end{array} }\right.$$$$\begin{array}{cc} \alpha t&\beta -\beta&\alpha t \end{array}$$$$\left.\vphantom{ \begin{array}{cc} \alpha t&\beta -\beta&\alpha t \end{array} }\right)$$0 < $$\alpha$$,$$\beta$$ < + $$\infty$$.

The eigenvalues of the matrix B(t) are $\alpha$t$\pm$i$\beta$, that is B(0) has purely imaginary eigenvalues, and therefore (1) is a nonhyperbolic system.

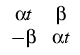
The aim of this project is to investigate the integral manifolds loosing their attractivity and, especially, to study their relations with the phenomenon of delayed loss of stability. In the hyperbolic case the existence of the integral manifolds of the form z = h(t, y,$\varepsilon$) has been known for a long time (see, e.g., [1]).

It is proved that under some general assumptions on the functions Y and Z, there exists a control function a(y,$\varepsilon$) such that system (1) has an integral manifold z = h(t, y,$\varepsilon$), where h is uniformly bounded. We note that this manifold is attractive for t < 0 and repulsive for t > 0. We call these manifolds loosing as manifolds their attractivity.

The question of the smoothness of the integral manifold and of the control function is investigated. By the induction method it is shown that if the functions Y(t, y, z,$\varepsilon$), Z(t, y, z, a,$\varepsilon$) have continuous and uniformly bounded partial derivatives with respect to the variables y, z, a,$\varepsilon$ up to the order k, then the integral manifold h(t, y,$\varepsilon$) and the control function a(y,$\varepsilon$) have continuous and uniformly bounded partial derivatives with respect to y up to the order k - 1.

References:

1. V.V. STRYGIN, V.A. SOBOLEV, Separation of Motions by the Integral Manifold Method, Nauka, Moscow, 1988.

2. K.R. SCHNEIDER, E.V. SHCHETININA, V.A. SOBOLEV, Integral manifolds loosing their attractivity, in preparation.

Project 4: Maximal temperature of safe combustion in case of an autocatalytic reaction

(K.R. Schneider).

Cooperation with: E.A. Shchepakina (Samara State University, Russia)

Description:

We consider the problem of thermal explosion of a gas mixture in case of an autocatalytic combustion reaction in a homogeneous medium. As a mathematical model we use the differential system

$\parbox{13cm}{ \begin{eqnarray*} \varepsilon \frac{d\Theta}{dt} & ... ...Theta, \\ \frac{d\eta}{dt} & = & \eta (1 - \eta ) e^{\Theta}. \end{eqnarray*}}$ $\parbox{1cm}{ \begin{eqnarray} \end{eqnarray}}$

Here, $\Theta$ denotes the temperature, $\eta$ is the depth of conversion of the gas mixture, - $\alpha$$\Theta$ describes the volumetric heat loss, and $\varepsilon$ is a positive parameter which is small in case of a highly exothermic reaction. There exists an exponentially small $\alpha$-interval A_{$\varepsilon$} : = ($\alpha_{0}^{}$($\varepsilon$),$\alpha_{1}^{}$($\varepsilon$)) containing $\alpha^{*}_{}$($\varepsilon$), where

$$\alpha^{*}_{}$$($$\varepsilon$$) = $$\alpha_{0}^{}$$ + $$\alpha_{1}^{}$$$$\varepsilon$$ + O($$\varepsilon^{2}_{}$$), $$\alpha_{0}^{}$$ = e/4, $$\alpha_{1}^{}$$ = - e/$$\sqrt{{2}}$$,

such that for $\alpha$ > $\alpha_{1}^{}$($\varepsilon$)($\alpha$ < $\alpha_{0}^{}$($\varepsilon$)) belongs to the slow regime (explosive regime). The interval A_{$\varepsilon$} characterizes the critical regime. For $\alpha$ $\in$ A, there are canard trajectories $\sum_{{\alpha ,\varepsilon}}^{}$(t) of system (1) starting at $\Theta$ = $\Theta_{0}^{}$ = 0, $\eta$ = $\eta_{0}^{}$ < 0.5, and satisfying $\sum_{{\alpha ,\varepsilon}}^{}$(t) $\rightarrow$ ($\eta$ = 1, $\Theta$ = 0) as t $\rightarrow$ $\infty$. Our goal is to estimate the maximal temperature $\Theta^{\varepsilon}_{{\max}}$ of the canard solution $\sum_{{\alpha ,\varepsilon}}^{}$(t) for $\alpha$ = $\alpha^{*}_{}$($\varepsilon$) and $\varepsilon$ sufficiently small. We derive an estimate and an asymptotic relation for $\Theta^{\varepsilon}_{{\max}}$ as $\varepsilon$ $\rightarrow$ 0 by means of a result on delayed exchange of stabilities in singularly perturbed systems derived by one of the authors ([1]).

References:

1. N.N. NEFEDOV, K.R. SCHNEIDER, On immediate-delayed exchange of stabilities and periodic forced canards, WIAS Preprint no. 872 , 2003.

2. K.R. SCHNEIDER, E.A. SHCHEPAKINA, Maximal temperature of safe combustion in case of an autocatalytic reaction, WIAS Preprint no. 890 , 2003.

[Next]:

Research Group Numerical Mathematics and Scientific

[Up]:

Projects

[Previous]:

Dynamics of semiconductor lasers

 [Contents] 

 [Index]