Collaborator: K. Gärtner
Cooperation with: O. Schenk (Universität Basel, IFI, Switzerland)
Description:
PARDISO is a SMP-parallel, direct solver for sparse linear systems
with coefficient matrices close to structural symmetry.
The development started within in the framework of the ETH-CRAY-SuperCluster
collaboration and was continued over the years by both authors.
PARDISO is well established
in some application areas and distributed via computer vendor libraries
(NEC, Compaq), too.
The activities during the year 2002 focused on:
- Porting to IA-32/IA-64 SMPs using up-to-date versions of Intel's OpenMP
Fortran compilers;
- Improvements for matrices far from structural symmetry
(see [1]);
- Two-level scheduling to improve the parallel efficiency due to a reduced
number of synchronization events without increasing the number of
operations [2];
- Application to some special saddle-point problems to estimate the effort for
a more general solution;
- Assistance for use in different IFI/WIAS applications.
The supported matrix types (complex and real, spd, Hermitian,
complex symmetric), the low operation count, the BLAS3 performance
reached during the factorization, and the fill-in close to ln(n) n
for 2D problems (n number of unknowns) make
PARDISO a workhorse for solving many (especially 2D) partial differential
equation problems.
An increased penetration speed of the code into WIAS application problems was
observed during 2002. To name a few: diffractive optics (see page
![[*]](http://www.wias-berlin.de/misc/icons/cross_ref_motif.gif)
), eigenvalue problems
for Maxwell's equations in microwave guides and lasers
(see page ), crystal growth
modeling (see page ).
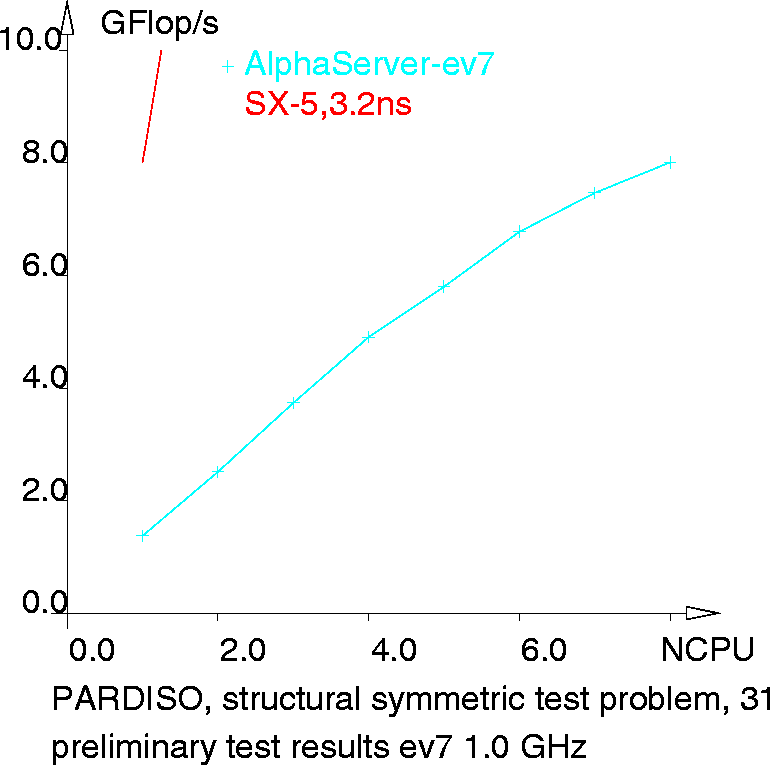
Within an evaluation of the new ev7-based HP-AlphaServer generation,
PARDISO was used, too. Typical (wall-clock) times are: a standard test
problem (Laplace equation on a triangular unstructured
grid with 151389 nodes) is factorized now in
0.9 sec on the 1.0 GHz single ev7
CPU, the 3D laser diode structural symmetric test problem (311819 unknowns)
can be solved on the 8 CPU configuration
in 6:13 min with parallel efficiency above 70 % without the two-level
scheduling. On the other hand that last number
is in the same range that could be reached on a single CPU SX-5 two years ago.
References:
- I.S. DUFF, J. KOSTER,
The design and use of algorithms for permuting
large entries to the diagonal of sparse matrices,
SIAM J. Matrix Anal. Appl., 20 (1999), pp. 889-901.
- O. SCHENK, K. GÄRTNER,
Two-level dynamic scheduling in PARDISO: Improved
scalability on shared memory multiprocessing systems,
Parallel Comput., 28 (2002), pp. 187-197.
LaTeX typesetting by I. Bremer
5/16/2003
