Estimates of the dimension for attractors

[Next]:

Long-time dynamics in adaptive gain control

[Up]:

Project descriptions

[Previous]:

Dynamics of semiconductor lasers

[Contents]

[Index]

Estimates of the dimension for attractors of evolutionary PDEs and homoclinic bifurcations

Collaborator: D. Turaev

Cooperation with: S. Zelik (Moscow State University, Faculty of Mathematics and Mechanics, Russia)

Description:

One of the great achievements of the theory of evolutionary PDEs is the theory of attractors of semiflows in infinite-dimensional spaces. Here, the main idea due to works of Ladyzhenskaja, Yorke, Vishik, Temam, Hale, and others is that although the phase space is infinite dimensional, all the orbits may be attracted by an invariant set A (the attractor) of a finite dimension, so that the dynamics can possibly be understood by methods of the qualitative theory of ordinary differential equations. The crucial question here is to get realistic estimates on the dimension of the attractor. The best known upper estimates are obtained by the Douady-Oesterle-Iljashenko method which yields the estimate

$\begin{displaymath} {\rm dim}_H A < k,\end{displaymath}$ (1)

provided the semiflow contracts k-dimensional volumes.

The only working method which has been used, until now, to obtain estimates from below employs the idea that ${\rm dim} A$ is greater than the dimension of the unstable manifold of any equilibrium state in A. However, there exist classes of equations for which the gap between the lower estimates obtained by this method and the upper estimate given by (1) is very large. The question whether estimate (1) is optimal is a longstanding problem in the theory.

The goal of our research was to resolve this problem. Our idea is that the upper estimate (1) must be sharp whenever the dynamics of the system is recurrent. Different to this situation is the case of gradient-like systems where the dynamics on the attractor is, in a sense, trivial and where the dimension of the unstable manifolds of the equilibria gives a correct estimate for the dimension of the attractor, no matter what the volume-contraction properties of the system are. Our approach is based on the ideas from [1] where the notion of effective dimension d_eff of homoclinic bifurcations was introduced and where it was argued that the maximal dimension of invariant sets which can be born at a homoclinic bifurcation must be equal to d_eff no matter how small a dimension of the unstable manifolds of the involved saddle equilibria is. This principle is known to hold true for many different examples of homoclinic bifurcations.

This idea yields a radically new and very powerful method of obtaining realistic lower estimates of the dimension of attractors of systems which are not gradient-like: If the dynamics is recurrent, then it is plausible that some homoclinic bifurcations can be detected. Therefore, the corresponding value of d_eff estimates dim A from below. We note that the definition of the effective dimension from [1] is strongly based on the volume contraction arguments, so that the lower estimates obtained by our method must be close to the upper estimate (1) indeed.

An important example of systems, where a tremendous gap exists between the upper estimate (1) and the usual lower estimates, is provided by a class of damped nonlinear hyperbolic equations

$\begin{displaymath} u_{tt} + \gamma u_t + Au + \Phi(u) + F(u,u_t) =0,\end{displaymath}$ (2)

where u is an element of an abstract Hilbert space H, the operator A is positive definite, self-adjoint, and has a compact inverse, $\Phi$ is a gradient-type nonlinearity, F is a bounded nonlinearity in an appropriate norm, $\gamma$ is a small parameter (damping). We assume that the nonlinear damping terms in F(u,u_t) are smaller than $\gamma u_t$ ,i.e. $\Vert F'_v(u,v)\Vert\ll \gamma$ in an appropriate norm. One can see that the best possible estimate from above to the dimension of the attractor which can be obtained here by volume-contraction arguments is

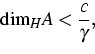$\begin{displaymath} {\rm dim}_H A < \frac{c}{\gamma},\end{displaymath}$ (3)

where c is some constant. On the other hand, the dimension of the unstable manifold of saddle equilibria which may exist here is bounded from above by a constant independent of $\gamma$ . Hence, when the damping constant $\gamma$ is small, the old methods give a very large gap between lower and upper estimates. Therefore, we choose this example to test our method.

In [2] we show that if system (2) is not gradient-like, then the following homoclinic bifurcation can typically be encountered: The system has an equilibrium state O of saddle type with one-dimensional unstable manifold W^u which contains two trajectories (separatrices) which leave O in opposite directions, one of these separatrices returns to O as $t\rightarrow +\infty$ , forming a homoclinic loop; moreover, it returns to O along the most stable direction. The spectrum of characteristic exponents of O has the following structure: One exponent, $\lambda_0$ ,is real and positive and bounded away from zero at small $\gamma$ , one exponent, $\lambda_1$ , is real and negative and bounded away from zero, and the rest of characteristic exponents are typically complex and have real parts of order $\gamma$ .

According to [1], the effective dimension of this homoclinic bifurcation is of order $\gamma^{-1}$ . In [2] we prove the following result.

Theorem. A d_eff/2-dimensional invariant torus densely filled with quasiperiodic trajectories can be born by an arbitrarily small smooth perturbation of the homoclinic loop under consideration.

Of course, such an invariant torus must lie in the attractor of the system so that the dimension of the attractor cannot be less than the dimension of this torus. Hence, we obtain the lower estimate comparable with the upper estimate (3), i.e. (3) cannot be improved. This proves, maybe contrarily to an intuitive believe, that unless the nonlinearity has a gradient-like structure, the dimension of the attractor of a weakly damped hyperbolic equation is extremely large and is given by (3). We stress again that such a kind of result is absolutely beyond the reach of the methods which existed before.

References:

D. TURAEV, On dimension of non-local bifurcational problems,
Bifurcation and Chaos, 6 (1996), pp. 123-156.
D. TURAEV, S. ZELIK, Homoclinic bifurcations and dimension of attractors of weakly damped hyperbolic equations,
in preparation.