Generalized electro-reaction-diffusion systems in heterostructures

[Next]:

Optimal control of surface heat treatments

[Up]:

Project descriptions

[Previous]:

On a nonlocal phase separation model

[Contents]

[Index]

Generalized electro-reaction-diffusion systems in heterostructures

Collaborator: A. Glitzky , R. Hünlich

Cooperation with: K. Gröger (Humboldt-Universität zu Berlin)

Supported by: DFG: ``Zur Analysis von thermodynamischen Modellen des Stoff-, Ladungs- und Energietransports in heterogenen Halbleitern'' (Analysis of thermodynamic models for the transport of mass, charge and energy in heterogeneous semiconductors)

Description: Models describing the transport of dopants in semiconducting materials via pair diffusion mechanisms are considered at very different modeling levels. Generally, such models contain continuity equations, a Poisson equation, and often nonlocal relations which express invariance properties such as global charge conservation. There exists a hierarchy of such models which is based on physically motivated assumptions concerning the time scales of different kinetic subprocesses (see [1, Chap. 5]). Starting from a basic model where all relevant species (electrons, holes, dopants, defects, and dopant-defect pairs) are balanced by continuity equations, one can finally reach a reduced model where only the total amount of each dopant is balanced. Most of such model equations at the different reduction levels can be written in a unified way as a generalized electro-reaction-diffusion system which we have studied last year. Many other problems in the field of electro-diffusion fit into this general setting, too.

We consider m species X_i where only the first l ones are assumed to underly drift-diffusion processes. Let z₀ denote the electrostatic potential, let $z=(z_0,\dots,z_k)$ , where the components z_j, $j=1,\dots,k$ , are some additional quantities representing the electrochemical potential of species eliminated by the foregoing model reduction. The functions $p_i(\cdot,z)$ are suitably chosen reference densities of the special structure

$\begin{displaymath} p_i(x,z)=p_{0i}(x)\,\mbox{e}^{P_i(z)}\,,\quad i=1,\dots,m\,.\end{displaymath}$

The problem is formulated in terms of the vector u of particle densities u_i, of the vector b of chemical activities b_i=u_i/p_0i, and of the vector z. The investigated model equations consist of m continuity equations

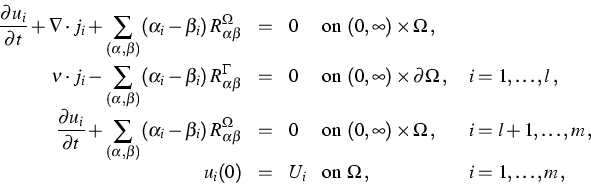$\begin{displaymath} \begin{array} {rclll} \displaystyle\frac{\partial u_i}{\part... ...\displaystyle \text{on } \Omega\,,&~ i=1,\dots,m\,,\end{array} \end{displaymath}$ (1)

which are coupled with a nonlinear Poisson equation

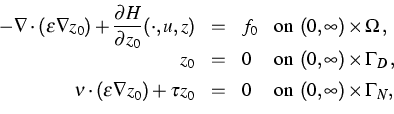$\begin{displaymath} \begin{array} {rcll} \displaystyle-\nabla\cdot (\varepsilon\... ... \displaystyle \text{on } (0,\infty)\times\Gamma_N,\end{array} \end{displaymath}$ (2)

and other nonlocal conservation laws

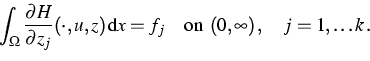$\begin{displaymath} \displaystyle \int_\Omega\frac{\partial H}{\partial z_j}(\cd... ...displaystyle \quad\text{on } (0,\infty)\,,\quad j=1,\dots k\,.\end{displaymath}$ (3)

Here $\varepsilon$ is the dielectric permittivity, f₀ is a fixed charge density, and f_j represent prescribed values of invariants. The function H is given by

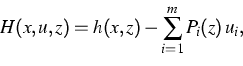
$\begin{displaymath} H(x,u,z)=h(x,z)-\sum_{i=1}^m P_i(z)\,u_i,\end{displaymath}$

with some function h which is determined by the reduction scheme. The particle fluxes for the mobile species X_i, $i=1,\dots,l$ ,have the form

$\begin{displaymath} j_i=-D_i(\cdot,b,z)p_{0i}\big[\nabla b_i+Q_i(z)\, b_i\nabla z_0\big],~ i=1,\dots,l\,,\end{displaymath}$

where $Q_i(z)= \tfrac{\partial P_i}{\partial z_0}(z)$ denote the charge numbers depending on the state z in our setting. The continuity equations contain volume source terms resulting from a lot of reversible reactions

$\begin{displaymath} \alpha_1X_1+\dots+\alpha_mX_m\rightleftharpoons \beta_1X_1+\dots +\beta_mX_m,\end{displaymath}$

where $\alpha,\,\beta\in \IZ^m_+$ are the vectors of stoichiometric coefficients. According to the mass action law, the corresponding reaction rates $R_{\alpha\beta}^\Omega$ are written as

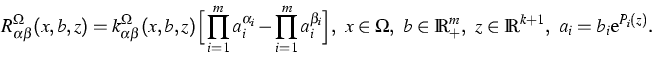
$\begin{displaymath} R_{\alpha\beta}^\Omega(x,b,z)= k^\Omega_{\alpha \beta}(x,b,z... ...Omega,~ b\in\IR^m_+,~z\in\IR^{k+1},~ a_i=b_i\mbox{e}^{P_i(z)}.\end{displaymath}$

For all immobile species X_i, $i=l+1,\dots,m$ , there should be a special reaction of the form

$\begin{displaymath} R_{\alpha\beta}^\Omega=k^\Omega_{\alpha \beta} \big[\prod_{j=1}^l a_j^{\alpha_j}-a_i^2\big].\end{displaymath}$

(4)

Additionally, we take into account boundary reactions between the mobile species with reaction rates $R_{\alpha\beta}^\Gamma$ .The kinetic coefficients D_i, $k^\Omega_{\alpha \beta}$ , and $k^\Gamma_{\alpha \beta}$ are allowed to depend on the space variable and on the state (b,z). Moreover, unlike our former investigations of electro-reaction-diffusion systems, also immobile species, initial densities U_i vanishing on sets of positive measure and nonsmooth data (heterostructures) are treated.

In [4] we proved an existence result for (1)-(3) at a special level in the hierarchy of pair diffusion models. But there we considered only homogeneous structures with smooth boundaries, and all species were assumed to be mobile. In [2] we derived global estimates for solutions of that model but now involving heterostructures and immobile dopants. The existence theory for these model equations is contained in [3].

In the weak formulation of (1)-(3), both the Poisson equation (2) and the nonlocal conservation laws (3) are formulated as a generalized Poisson equation ${\cal E}(z,u)=0$ . For every fixed u, the operator ${\cal E}(\cdot,u)$ is a strongly monotone potential operator. By means of the potential of this operator and of the usual chemical ansatz, the free energy functional

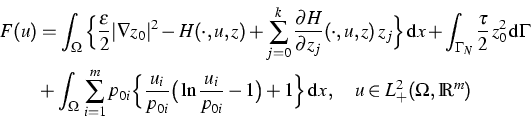
$\begin{displaymath} \begin{split} F(u)&=\int_\Omega\Big\{\frac{\varepsilon}{2}\v... ...+1\Big\}\,\text dx\,, \quad u\in L^2_+(\Omega,\IR^m)\end{split}\end{displaymath}$

is derived, where z is the unique solution of ${\cal E}(z,u)=0$ . The functional F turns out to be a Ljapunov functional. Under the assumption of no false equilibria in the sense of Prigogine, there is a thermodynamic equilibrium which is uniquely defined by the structure of the stoichiometric subspace and by the initial state. Exploiting the existence of reactions of the form (4), an estimate of the free energy by the dissipation rate

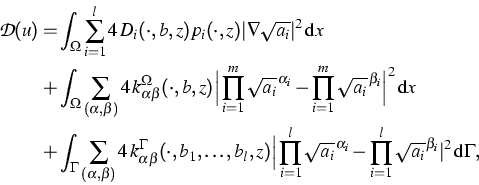
$\begin{displaymath} \begin{split} {\cal D}(u)=& \displaystyle\int_\Omega \displa... ...i=1}^l\sqrt{a_i}^{\,\beta_i}\vert^2 \,\text d\Gamma,\end{split}\end{displaymath}$

where ${\cal E}(z,u)=0$ , b_i=u_i/p_0i, $a_i=b_i\,\text{e}^{P_i(z)}$ , guarantees the exponential decay of the free energy along trajectories. This leads to essential tools for the proof of global upper bounds of solutions. Starting with two preliminary estimates, a Moser iteration scheme supplies the global bounds for the particle densities of the mobile species. Then a corresponding assertion for the immobile species can be obtained straightforward. Using these global estimates, the exponential decay of densities u_i, chemical activities b_i, and potentials z₀ and z_j to their equilibrium values can be verified.

For the existence proof we carry out two steps of regularization and consider problems ( $\mbox{P}_N$ ) and ( $\mbox{P}_M$ ). The first step ( $\mbox{P}_N$ ) contains regularizations in the volume and boundary reaction terms of the continuity equations only. By means of energy estimates and Moser iteration we derive a priori estimates which are independent of the regularization level N. A further regularization in the drift terms of ( $\mbox{P}_N$ ) leads to a problem ( $\mbox{P}_M$ ). The existence of solutions of ( $\mbox{P}_M$ )follows by two fixed-point iterations (Banach's fixed-point theorem for the equations of the immobile species, Schauder's fixed-point theorem for the equations of the mobile species). Moreover, we verify estimates for the solutions of ( $\mbox{P}_M$ )which are independent of the regularization level M which finally leads to the existence result.

The presented results concerning the generalized electro-reaction-diffusion system (1)-(3) and their proofs can be found in [1, Chap. 8].

References:

A. GLITZKY, Elektro-Reaktions-Diffusionssysteme mit nichtglatten Daten, habilitation thesis, Humboldt-Universität zu Berlin, 2001.
A. GLITZKY, R. HÜNLICH, Global properties of pair diffusion models, Adv. Math. Sci. Appl., 11 (2001), pp. 293-321.
$\dito$ , On an existence result for pair diffusion models, in preparation.
W. MERZ, A. GLITZKY, R. HÜNLICH, K. PULVERER, Strong solutions for pair diffusion models in homogeneous semiconductors, Nonlinear Anal. Real World Appl., 2 (2001), pp. 541-567.