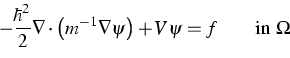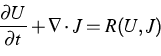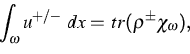Collaborator: M. Baro
,
H.-Chr. Kaiser
,
H. Neidhardt
,
J. Rehberg
Supported by: DFG: ``Kopplung von van Roosbroeck- und
Schrödinger-Poisson-Systemen mit Ladungsträgeraustausch''
(Coupling between van Roosbroeck system and a
Schrödinger-Poisson system including exchange of carriers)
Description:
The general goal of this research is the modeling of semiconductor multi
quantum well lasers on
the basis of a mixed model: One part is governed by van Roosbroeck's
system while a neighborhood of the
active zone is described by quantum mechanics. To that end we aim at
an embedding of a quantum mechanically described structure into a
macroscopic flow. The problem is that usually in quantum mechanics
selfadjoint Schrödinger operators (including selfadjoint boundary
conditions) are regarded, but selfadjoint Schrödinger operators
necessarily lead to vanishing currents within the substructure. This
consequence, however, is unacceptable from a physical point of view.
Having in mind a current continuity condition for both the quantum and
macroscopic current, in [6]/[7] the following setup for
the description of an open quantum system
driven by an adjacent macroscopic flow was proposed:
Let the open quantum system be situated in a bounded spatial domain
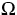 of
of 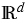 ,
, 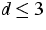 .There we regard the Schrödinger equation
.There we regard the Schrödinger equation
| 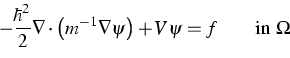 |
(1) |
with a mass tensor m, a complex-valued potential V, and the
boundary condition
| 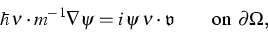 |
(2) |
where 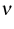 denotes the outer unit normal on
denotes the outer unit normal on 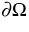 .This system is partly driven by an adjacent macroscopic flow acting on
the boundary
.This system is partly driven by an adjacent macroscopic flow acting on
the boundary 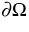 of
of 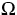 . The macroscopic flow is
assumed to be of the form
. The macroscopic flow is
assumed to be of the form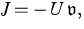 where U is the density of the macroscopic transport quantity and
where U is the density of the macroscopic transport quantity and
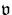 is the corresponding velocity density. In particular,
we have in mind a gradient flow
is the corresponding velocity density. In particular,
we have in mind a gradient flow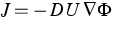 with
with 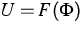 which is governed by a
reaction-diffusion equation
which is governed by a
reaction-diffusion equation
| 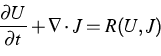 |
(3) |
in a neighborhood of 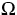 .
With non-smooth coefficients and mixed boundary conditions such an
equation allows only for little regularity of the flow it governs
([1]). That is why we make only weak assumptions on the
regularity of the flow acting on the boundary of
.
With non-smooth coefficients and mixed boundary conditions such an
equation allows only for little regularity of the flow it governs
([1]). That is why we make only weak assumptions on the
regularity of the flow acting on the boundary of 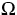 .The crucial point is that the boundary condition (2) cannot
be implemented by using the usual boundary integral within the weak
formulation, but has to be defined by a more subtle form approach, due
to the deficient regularity of the adjacent macroscopic flow.
Additionally, non-vanishing imaginary parts of the Schrödinger
potentials, reflecting absorptive and dispersive properties of the
substrate, have to be included in this context. Naturally, in a first
step, the spectral properties of the--essentially
non-selfadjoint--Schrödinger operators are of interest. The
abstract framework for the rigorous definition and spectral analysis
of the Schrödinger-type operator (1), (2)
is the form perturbation method with a symmetric principal part and a
non-symmetric part which is form-subordinated to it. In [4]
under minimal (and realistic ([1])) assumptions on the
macroscopic flow, the following assertions about the thus defined
Schrödinger operator have been proven:
.The crucial point is that the boundary condition (2) cannot
be implemented by using the usual boundary integral within the weak
formulation, but has to be defined by a more subtle form approach, due
to the deficient regularity of the adjacent macroscopic flow.
Additionally, non-vanishing imaginary parts of the Schrödinger
potentials, reflecting absorptive and dispersive properties of the
substrate, have to be included in this context. Naturally, in a first
step, the spectral properties of the--essentially
non-selfadjoint--Schrödinger operators are of interest. The
abstract framework for the rigorous definition and spectral analysis
of the Schrödinger-type operator (1), (2)
is the form perturbation method with a symmetric principal part and a
non-symmetric part which is form-subordinated to it. In [4]
under minimal (and realistic ([1])) assumptions on the
macroscopic flow, the following assertions about the thus defined
Schrödinger operator have been proven:
- 1.
- Its resolvent belongs to the same summability class as the
resolvent of the free Hamiltonian (with Neumann boundary
conditions).
- 2.
- It generates an analytic semigroup on L2.
- 3.
- It has no real eigenvalues and is, consequently, completely
non-selfadjoint.
- 4.
- In the two- and three-dimensional case there is an Abel basis
of root vectors in L2; in the one-dimensional
case one obtains a Riesz basis of root vectors.
- 5.
- If the non-selfadjoint Schrödinger operator is dissipative,
then the imaginary part
of the potential must be positive, and the boundary form is given by
a positive measure times the imaginary unit.
In the situation of a closed quantum system the Schrödinger-Poisson
system ([2], [3], [6], [7]) turned
out to give an adequate description of the occurring physical quantities
such as carrier densities and electrostatic potential. This was the
reason for our attempt to re-establish a Schrödinger-Poisson system
in the situation of an open quantum system. At first, physical notions
as carrier and current densities have to be re-defined in the case
of open quantum systems. The key for doing so is the observation that
the open quantum system always may be embedded by dilation theory into
a closed one at least if the corresponding Hamiltonian is dissipative
(or anti-dissipative) ([4]). In the spatially one-dimensional
case the enlarged Hilbert space and the corresponding selfadjoint
operator admit an explicit description ([5]), this is why we
first investigated this situation. In [5]
the required dilation of the non-selfadjoint Schrödinger operator is
performed, the characteristic function is determined and a
(generalized) eigenfunction expansion is carried out. On the basis of
this,
the fundamental notions of steady state, carrier density, and current density
can be defined, and the concept of a dissipative Schrödinger-Poisson
system can be
established. The electron/hole densities u+, u- are determined
by
| 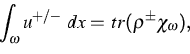 |
(4) |
where 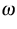 is any Borel subset of the interval
is any Borel subset of the interval 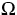 , and
, and
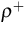 ,
, 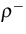 are density matrices, related to the
Schrödinger-type operators (1)-(2) for holes and
electrons, respectively, which act on the Hilbert space
are density matrices, related to the
Schrödinger-type operators (1)-(2) for holes and
electrons, respectively, which act on the Hilbert space
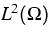 . The dependence of the carrier density on the
Schrödinger potential has been investigated concerning estimates
and continuity properties. Having these things at hand, we intend to
prove the existence of a solution for the dissipative
Schrödinger-Poisson system.
. The dependence of the carrier density on the
Schrödinger potential has been investigated concerning estimates
and continuity properties. Having these things at hand, we intend to
prove the existence of a solution for the dissipative
Schrödinger-Poisson system.
References:
- J.A. GRIEPENTROG, H.-CHR. KAISER, J. REHBERG, Heat
kernel and resolvent properties for second order elliptic differential
operators with general boundary conditions in Lp, Adv. Math. Sci.
Appl., 11 (2001), pp. 87-112.
- F. NIER, A
stationary Schrödinger-Poisson system arising from the modelling
of electronic devices, Forum Math., 2 (1990),
pp. 489-510.
-
 , A variational formulation of
Schrödinger-Poisson systems in dimensions
, A variational formulation of
Schrödinger-Poisson systems in dimensions 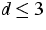 ,
Comm. Partial Differential Equations, 18 (1993),
pp. 1125-1147.
,
Comm. Partial Differential Equations, 18 (1993),
pp. 1125-1147.
- H.-CHR. KAISER, H. NEIDHARDT, J. REHBERG,
Macroscopic current induced boundary conditions for
Schrödinger operators, WIAS Preprint no. 650, 2001, to appear in:
Integral Equations Oper. Theory.
-
 , On
1-dimensional dissipative Schrödinger-type operators, their
dilations and eigenfunction expansions, WIAS Preprint no.
664, 2001.
, On
1-dimensional dissipative Schrödinger-type operators, their
dilations and eigenfunction expansions, WIAS Preprint no.
664, 2001.
- H.-CHR. KAISER, J. REHBERG, About a one-dimensional
stationary Schrödinger-Poisson system with Kohn-Sham potential,
Z. Angew. Math. Phys., 50 (1999), pp. 423-458.
-
 , About a stationary
Schrödinger-Poisson system with Kohn-Sham potential in a bounded
two- or three-dimensional domain, Nonlinear Anal.,
41A (2000), pp. 33-72.
, About a stationary
Schrödinger-Poisson system with Kohn-Sham potential in a bounded
two- or three-dimensional domain, Nonlinear Anal.,
41A (2000), pp. 33-72.
LaTeX typesetting by I. Bremer
9/9/2002
![]() of
of ![]() ,
, ![]() .There we regard the Schrödinger equation
.There we regard the Schrödinger equation