Bearbeiter: W. Dreyer
,
F. Duderstadt
Kooperation: S. Eichler (Freiberger Compound Materials GmbH, Freiberg)
Förderung: Freiberger Compound Materials GmbH (FCM) (Freiberg)
Beschreibung der Forschungsarbeit:
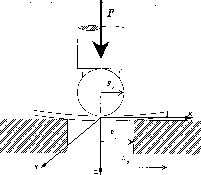 Gemäß der nebenstehenden Abbildung
führt die FCM Bruchtests mit
runden GaAs-Waferplatten durch. Im Test liegen die Platten
konzentrisch auf einem Stützring. Die Last F wird durch einen
kugelförmigen Stempel aufgebracht. Das WIAS berechnet für
vorgegebene Last alle in der Waferplatte auftretenden Spannungsfelder
sowie die Durchbiegung der Waferplatte. Hieraus werden die für die
Bruchfestigkeit bedeutsamen maximalen Zugspannungen und die maximale
Durchbiegung ermittelt.
Gemäß der nebenstehenden Abbildung
führt die FCM Bruchtests mit
runden GaAs-Waferplatten durch. Im Test liegen die Platten
konzentrisch auf einem Stützring. Die Last F wird durch einen
kugelförmigen Stempel aufgebracht. Das WIAS berechnet für
vorgegebene Last alle in der Waferplatte auftretenden Spannungsfelder
sowie die Durchbiegung der Waferplatte. Hieraus werden die für die
Bruchfestigkeit bedeutsamen maximalen Zugspannungen und die maximale
Durchbiegung ermittelt.
Der Berechnung liegen die folgenden Annahmen zugrunde:
- Die GaAs-Platte wird als kubisch anisotropes elastisches Material
behandelt. Die (001) Richtung fällt mit der Lastrichtung zusammen.
- Die Übertragung der Last F mittels der Kugel führt zu
einer Kontaktfläche Kugel/Wafer, deren Größe mit der
Theorie Hertz'scher Pressung für anisotrope Materialien
berechnet wird. Diese Theorie liefert außerdem die
Druckverteilung auf der Kontaktfläche.
- Der Stützring wird als starr angenommen.
- Die Verhältnisse an der Kontaktfläche
Stützring/Wafer bei RA werden derart modelliert, dass hier
die Durchbiegung null sein soll und dass die Waferplatte hier kein
Biegemoment aufnimmt.
Die Variablen sind die rechtwinklig kartesischen Komponenten 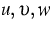 der Verschiebung sowie die Querkräfte
der Verschiebung sowie die Querkräfte 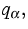
 . Die Verschiebungen haben für schubsteife dünne
Platten in Lagrange'schen Koordinaten
X,Y,Z die Darstellung
. Die Verschiebungen haben für schubsteife dünne
Platten in Lagrange'schen Koordinaten
X,Y,Z die Darstellung
| 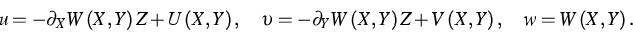 |
(1) |
Die Feldgleichungen für diese Variablen basieren auf den
Gleichgewichtsbedingungen
| 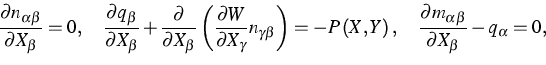 |
(2) |
wo die Funktion 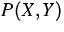 die an der Kontaktfläche zwischen
Druckkugel und Platte entsprechend der Hertz'schen Theorie wirkende
Flächenlast ist. Die Komponenten des Schnittkrafttensors
die an der Kontaktfläche zwischen
Druckkugel und Platte entsprechend der Hertz'schen Theorie wirkende
Flächenlast ist. Die Komponenten des Schnittkrafttensors 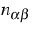 und des Schnittmomententensors
und des Schnittmomententensors 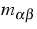 lauten für
ein einkristallines Material mit kubischer Kristallsymmetrie
lauten für
ein einkristallines Material mit kubischer Kristallsymmetrie
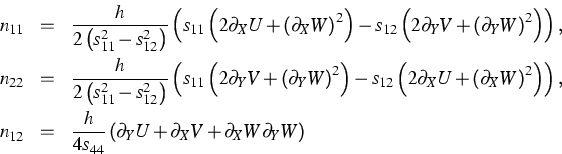
sowie
| 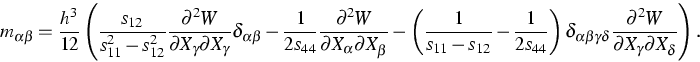 |
(3) |
Hier bezeichnet h die Dicke der Platte, und die Konstanten s11, s12 und s44 sind die unabhängigen Komponenten der
Nachgiebigkeitsmatrix.
Die Randbedingungen für dieses System sind
| 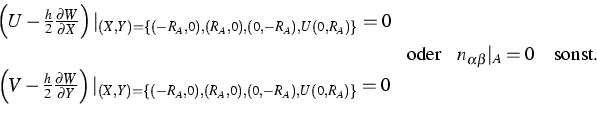 |
(4) |
| 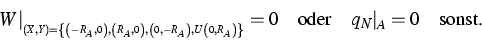 |
(5) |
Eine Kontrollrechnung mit diesen Randbedingungen, die eine 4-Punkt-Auflage
mit drehbarer Lagerung simulieren, führte bei den vorliegenden
Materialdaten zu dem Ergebnis W>0, was aber durch den Auflagering
verhindert wird. Somit ist
| 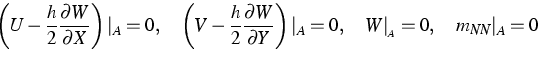 |
(7) |
die natürliche Randbedingung, welche ausdrückt: Die Platte liegt
vollständig drehbar auf dem Auflagering.
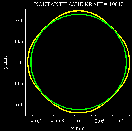 Die Berechnung der Flächenlast P (X, Y) setzt die Lösung des
Kontaktproblems Druckkugel/Waferplatte entsprechend der Hertz'schen
Theorie voraus. Die nebenstehende Abbildung zeigt die entstehende
Kontaktfläche, die eine Kugel aus isotropem
Material auf einer einkristallinen Platte
mit kubischer Symmetrie induziert. Der ebenfalls eingezeichnete Kreis
entsteht durch Isotropisierung der drei elastischen Konstanten in der
Voigt'schen Näherung.
Die Berechnung der Flächenlast P (X, Y) setzt die Lösung des
Kontaktproblems Druckkugel/Waferplatte entsprechend der Hertz'schen
Theorie voraus. Die nebenstehende Abbildung zeigt die entstehende
Kontaktfläche, die eine Kugel aus isotropem
Material auf einer einkristallinen Platte
mit kubischer Symmetrie induziert. Der ebenfalls eingezeichnete Kreis
entsteht durch Isotropisierung der drei elastischen Konstanten in der
Voigt'schen Näherung.
Gelöst wird das beschriebene System mit finiten Elementen, wobei
Dreieckselemente mit unterschiedlichen Ansätzen für das Problem
(2)1, (3) und für das Problem (2)2, 3, (5) auf einem Netz
verwendet werden müssen. Das erstere Problem wird mit
C2-Hermite'schen Ansatzfunktionen gerechnet, während wir für das
zweite Problem C1-Hermite'sche Ansatzfunktionen verwendet
haben. Mit Simplexelementen ist das hier vorgestellte Plattenproblem
auch in 3D nicht lösbar.
Bis zum Redaktionsschluss waren die Arbeiten noch nicht
abgeschlossen.
LaTeX typesetting by I. Bremer
4/30/2001
 Gemäß der nebenstehenden Abbildung
führt die FCM Bruchtests mit
runden GaAs-Waferplatten durch. Im Test liegen die Platten
konzentrisch auf einem Stützring. Die Last F wird durch einen
kugelförmigen Stempel aufgebracht. Das WIAS berechnet für
vorgegebene Last alle in der Waferplatte auftretenden Spannungsfelder
sowie die Durchbiegung der Waferplatte. Hieraus werden die für die
Bruchfestigkeit bedeutsamen maximalen Zugspannungen und die maximale
Durchbiegung ermittelt.
Gemäß der nebenstehenden Abbildung
führt die FCM Bruchtests mit
runden GaAs-Waferplatten durch. Im Test liegen die Platten
konzentrisch auf einem Stützring. Die Last F wird durch einen
kugelförmigen Stempel aufgebracht. Das WIAS berechnet für
vorgegebene Last alle in der Waferplatte auftretenden Spannungsfelder
sowie die Durchbiegung der Waferplatte. Hieraus werden die für die
Bruchfestigkeit bedeutsamen maximalen Zugspannungen und die maximale
Durchbiegung ermittelt.
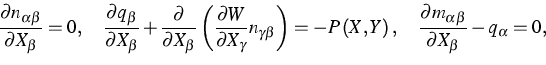
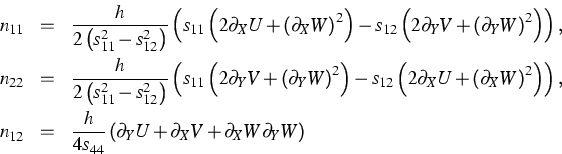
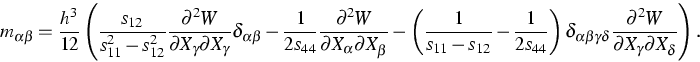
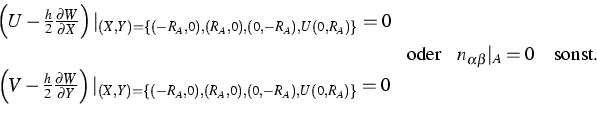
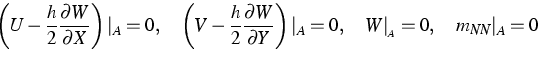
 Die Berechnung der Flächenlast P (X, Y) setzt die Lösung des
Kontaktproblems Druckkugel/Waferplatte entsprechend der Hertz'schen
Theorie voraus. Die nebenstehende Abbildung zeigt die entstehende
Kontaktfläche, die eine Kugel aus isotropem
Material
Die Berechnung der Flächenlast P (X, Y) setzt die Lösung des
Kontaktproblems Druckkugel/Waferplatte entsprechend der Hertz'schen
Theorie voraus. Die nebenstehende Abbildung zeigt die entstehende
Kontaktfläche, die eine Kugel aus isotropem
Material