Spin-Gläser und Neuronale Netze

[Next]:

Stochastische Dynamik ungeordneter Mean-Field-Modelle

[Up]:

Projektbeschreibungen

[Previous]:

Tieftemperaturphasen in Modellen mit langreichweitiger Wechselwirkung

[Contents]

[Index]

Spin-Gläser und Neuronale Netze

Bearbeiter: A. Bovier , B. Gentz , B. Niederhauser (Graduiertenkolleg)

Kooperation: V. Gayrard (CPT-Marseille), D. Mason (University of Delaware), A. C. D. van Enter (RU Groningen), M. Löwe (EURANDOM, Eindhoven)

Beschreibung der Forschungsarbeit:

Eine ausführliche Darstellung der Fragestellungen, denen wir uns in diesem Projekt widmen, wurde im Jahresbericht 1994 gegeben. Ein umfangreicher Übersichtsartikel ist soeben erschienen [1], eine elementarere Zusammenfassung ist in [2] zu finden.

Das Hauptziel der Arbeiten der vergangenen Jahre lag in der Konstruktion extremaler Gibbs-Maße für Hopfield-artige Modelle und der Untersuchung ihrer Eigenschaften. Dabei wurde üblicherweise in der Konstruktion des thermodynamischen Limes ein symmetriebrechender Term (,,äußeres Magnetfeld``) eingeführt. Die wesentliche technische Schwierigkeit bestand dann darin, nachzuweisen, daß dieser Term stochastische Einflüsse übertraf. Eine offene Frage blieb bisher die, das Konvergenzverhalten der Gibbszustände ohne symmetriebrechenden Term in Situationen mit unendlich vielen extremalen Maßen zu beschreiben. Diese Fragen sind aber zentral, will man die eigentlichen Besonderheiten echter Spin-Glas-Zustände verstehen lernen. Dieser Punkt ist in jüngster Zeit insbesondere von Newman und Stein [3] hervorgehoben worden. Auch in einer neuen Arbeit von Talagrand [4] wird dies deutlich.

In diesem Jahr gelang es uns in zwei vergleichsweise noch einfachen Beispielen, diese Frage zu beantworten. In [5] wurde der Fall eines Hopfield-Modells mit zwei Gaußschen Mustern betrachtet. Die Menge der extremalen Maße ist hier überabzählbar und wird durch die Punkte auf einem Kreis indiziert. Mit Hilfe eines expliziten symmetriebrechenden Terms kann jedes dieser Maße als Grenzwert konstruiert werden. Ohne einen solchen wird, wie gezeigt werden konnte, durch die Unordnung eine stochastische Symmetriebrechung produziert, die dazu führt, daß in jedem (großen) endlichen Volumen gerade ein Paar von extremalen Maßen im wesentlichen das Gibbs-Maß dominiert, welches aber sowohl vom Zufall als auch vom Volumen abhängt. Damit wurde ein Beispiel für das sogenannte ,,chaotic pairs picture`` von Newman und Stein konstruiert. Ein weiteres Beispiel liefert das gewöhnliche Hopfield-Modell selbst, wobei aus technischen Gründen relativ starke Einschränkungen an das Wachstumsverhalten der Musterzahl als Funktion der Systemgröße gemacht werden mußten. In dieser Situation können die Gibbs-Maße Q_N im Volumen N asymptotisch zerlegt werden in der Form

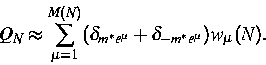
$\begin{displaymath} Q_N\approx \sum_{\mu=1}^{M(N)} (\delta_{m^*e^\mu}+\delta_{-m^*e^\mu}) w_\mu(N).\end{displaymath}$

Dabei sind die Gewichte von der Form

$\begin{displaymath} w_\mu(N)\approx\exp(\sqrt {M(N)} B_\mu(N)),\end{displaymath}$

wo $B_\mu(N)$ explizit bekannte, austauschbare und schwach korrelierte Zufallsvariablen mit Varianz 1 sind. Die Aufgabe ist somit, die extremale Ordnungsstatistik der Zufallsvariablen $B_\mu$ zu analysieren. In einer Arbeit mit D. Mason [6] wurde dieses Problem unter Zuhilfenahme von starken Gaußschen Kopplungstechniken gelöst. Es wurde gezeigt, daß die Variablen sich im Hinblick auf ihre Extrema asymptotisch wie unabhängige Gaußsche Zufallsvariablen verhalten. Hieraus folgt dann wiederum, daß für gegebenes N mit Wahrscheinlichkeit nahe bei Eins ein zufälliger Index $\mu(N)$ die Summe dominiert, d. h. $w_{\mu(N)}(N)\approx 1$ .

Eine weitere für Unordnungseffekte sensitive Größe sind die Fluktuationen der Ordnungsparameter. Dabei erweist sich die Untersuchung des Verhaltens an der kritischen Temperatur als besonders interessant. Schon im Fall endlich vieler Patterns [7] stellt sich heraus, daß hier ein sehr ungewöhnlicher Grenzwertsatz gilt: die Verteilung der Fluktuationen des Overlapparameters konvergiert nämlich - auch nicht nach Zentrierung - nicht mehr fast sicher gegen eine deterministische Grenzverteilung, sondern nur noch in Verteilung gegen eine - explizit angebbare - zufällige Verteilungsfunktion. Offensichtlich spürt das System am kritischen Punkt bereits die ,,Nähe`` zur Spin-Glas-Phase. Von großem Interesse ist nun natürlich, zu verfolgen was passiert, wenn die Patternzahl wächst. Ein erstes Resultat, basierend auf den auch in [6] verwendeten Kopplungssätzen, wurde dazu in [8] bewiesen.

Projektliteratur:

A. BOVIER, V. GAYRARD, Hopfield models as generalized random mean-field models, in: Mathematical Aspects of spin glasses and neural networks (A. Bovier, P. Picco, Hrsg.), Progress in Probability, Vol. 41, pp. 3-91, Birkhäuser, Boston-Basel-Berlin, 1998.
$\dito$ , Statistical mechanics of neural networks: The Hopfield model and the Kac-Hopfield model, Markov Proc. Rel. Fields, 3 (1997), pp. 392-422.
C. M. NEWMAN, D. L. STEIN, Thermodynamic chaos and the structure for short-range spin glasses, in: Mathematical Aspects of spin glasses and neural networks (A. Bovier, P. Picco, Hrsg.), Progress in Probability, Vol. 41, pp. 187-243, Birkhäuser, Boston-Basel-Berlin, 1998.
M. TALAGRAND, Rigorous low temperature results for the mean field p-spins interaction model, Preprint, 1998.
A. BOVIER, A. C. D. VAN ENTER, B. NIEDERHAUSER, Stochastic symmetry-breaking in a Gaussian Hopfield model, WIAS-Preprint No. 416, 1998, erscheint in: J. Statist. Phys., 95 (1999).
A. BOVIER, D. M. MASON, Extreme value behaviour in the Hopfield model, in Vorbereitung.
B. GENTZ, M. LÖWE, The fluctuation of the overlap in the Hopfield model with finitely many patterns, erscheint in: Probab. Theory Related Fields (1998).
$\dito$ , Fluctuations in the Hopfield model at the critical temperature, WIAS-Preprint No. 461, 1998, eingereicht bei: Markov Proc. Rel. Fields (1998).