Simulation von monolithisch integrierten Mikrowellenschaltungen und

[Next]:

Adaptive Verfahren für Transportprozesse in porösen

[Up]:

Projektbeschreibungen

[Previous]:

pdelib - Algorithmen und Softwarekomponenten für

[Contents]

[Index]

Simulation von monolithisch integrierten Mikrowellenschaltungen und Multi-Chip-Moduln

Bearbeiter: G. Hebermehl , R. Schlundt

Kooperation: W. Heinrich, M. Kunze, T. Tischler, H. Zscheile (Ferdinand-Braun-Institut für Höchstfrequenztechnik), W. Bruns (Technische Universität Berlin)

Beschreibung der Forschungsarbeit: Die Arbeiten zur Simulation von Mikrowellenschaltungen wurden fortgesetzt. Der wachsende Markt für die Mobilkommunikation, die Sensor- und Radartechnik stimuliert die Entwicklung verbesserter und akkurat arbeitender Tools zur Berechnung der Eigenschaften individueller monolithisch integrierter Chips (MMICs), von Multi-Chip-Moduln und Gehäusen.

Die zu untersuchenden Strukturen können als Verbindung unendlich langer Wellenleiter beschrieben werden, die longitudinal homogen sind. Die Koppelung (die sogenannte Diskontinuität) der Wellenleiter ist von beliebiger Struktur. Einlaufende Moden werden in der Diskontinuität verändert. Das Verhalten der Moden der Struktur wird durch eine Streumatrix beschrieben, die aus der orthogonalen Dekomposition

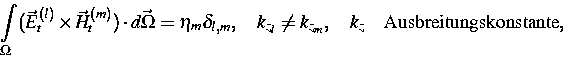
$\begin{displaymath} \int\limits_{\Omega}(\vec {E}_{t}^{(l)} \times \vec {H}_{t}^... ... \ne k_{z_{m}}, \quad k_{z} \quad \mbox{Ausbreitungskonstante},\end{displaymath}$

des elektrischen Feldes an zwei benachbarten Schnittebenen auf jedem Wellenleiter für eine Anzahl linear unabhängiger Erregungen extrahiert wird.

Um das elektromagnetische Feld und damit die Streumatrix berechnen zu können, wird ein dreidimensionales Randwertproblem für die Integralform der Maxwellschen Gleichungen formuliert. Zu den Maxwellschen Gleichungen werden die konstitutiven Relationen addiert. Durch die Einführung magnetischer Ladungen und damit magnetischer Stromdichten in die Maxwellschen Gleichungen wurde das Modell erweitert, so daß auch Perfect-Matched-Layer-Anisotropic-Absorber-Randbedingungen (spezielle Absorbing-Boundary-Bedingungen) berücksichtigt werden, um offene Strukturen besser behandeln zu können:

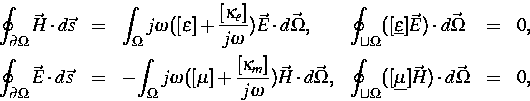
$\begin{displaymath} \begin{array} {llllll} \displaystyle{\oint_{\partial \Omega}... ... \vec \Omega} & \displaystyle{=} & \displaystyle{0},\end{array}\end{displaymath}$

$\begin{displaymath} \vec B = [\mu] \vec H, \quad \vec D = [\epsilon] \vec E, \qu... ...c J = [{\kappa}_e] \vec E, \quad \vec G = [{\kappa}_m] \vec H .\end{displaymath}$

Im Falle der Absorbing-Boundary-Bedingungen sind die Permeabilität $[\mu]$ , die Permittivität $[\epsilon]$ und die Konduktivitäten $[\kappa_{e}]$ sowie $[\kappa_{m}]$ Tensoren, sonst skalare Funktionen des Ortes. Wenn die Leitfähigkeit Null ist, haben wir ein reelles Problem zu lösen, anderenfalls sind alle Rechnungen im Komplexen durchzuführen.

An den Toren ist das transverse elektrische Feld gegeben durch die Superposition der transversalen Wellenleitermoden, die noch zu berechnen sind, bevor das Randwertproblem gelöst werden kann (Wellenleiter-Randbedingung). Alle anderen Teile des Randes werden als elektrische oder magnetische Wand interpretiert. Im Fall der Absorbing-Boundary-Bedingungen werden an diesen Teilen des Randes mehrere Schichten mit anisotropem Material definiert, in denen sich die auslaufenden Wellen abschwächen:

$\begin{displaymath} \vec E_{t}(z_{p}) = \sum\limits^{m^{(p)}}_{l=1} w_{l}(z_{p})... ...\quad \frac{[\epsilon]}{{\epsilon}_0} = \frac{[\mu]}{{\mu}_0} .\end{displaymath}$

Die Simulation der Schaltungen stellt extreme Anforderungen an die räumliche Auflösung, da neben Details im Submikrometerbereich Abmessungen im Millimeterbereich zu erfassen sind. Zur Einteilung des Gebietes werden nichtäquidistante Quadergitter verwendet. Die Diskretisierung der Gleichungen erfolgt mit Hilfe einer Finite-Volumen-Methode und führt auf hochdimensionale lineare Gleichungssysteme mit schwachbesetzten indefiniten reellen oder komplexen symmetrischen Koeffizientenmatrizen.

Auf Grund der longitudinalen Homogenität der Wellenleiter wird von einem exponentiellen Ansatz für die longitudinale Richtung ausgegangen:

$\begin{displaymath} \vec {E}(x,y,z\pm2h) = \vec {E}(x,y,z) e^{\mp j k_{z} 2h}.\end{displaymath}$

Die Substitution dieses Ansatzes in das lineare Gleichungssystem für die Berechnung der Wellenleiter-Randbedingung ergibt zusammen mit der Eliminierung der longitudinalen Komponenten des elektrischen Feldes unter Verwendung der elektrischen Divergenzgleichung ein schlecht konditioniertes Eigenwertproblem mit schwachbesetzten nichtsymmetrischen reellen oder komplexen (verlustbehafteter Fall) Matrizen zur Berechnung der ausbreitungsfähigen Moden k_z:

$\begin{displaymath} C \underline {\vec e} = \gamma \underline {\vec e}, \quad \gamma =-4 \sin^{2}(k_{z} h).\end{displaymath}$

Im Falle entarteter Eigenwerte wird eine Gram-Schmidt-Orthogonalisierung für die Eigenfunktionen bezüglich der Orthogonalitätsbedingung durchgeführt.

Mit Hilfe des Independent Set Orderings wird eine Ähnlichkeitstransformation des Eigenwertproblems vorgenommen und dadurch eine Aufspaltung der während der inversen Iteration im Arnoldi-Verfahren zu lösenden linearen Gleichungssysteme erreicht.

Durch die Verwendung von vier verschiedenen Arten auf die Aufgabe zugeschnittener Vorkonditionierer, insbesondere durch die Verbesserung des Independent Set Orderings, konnten die Rechenzeiten für die Lösung der linearen Gleichungssysteme (3*10⁶ Unbekannte) in Zusammenhang mit Krylov-Verfahren weiter reduziert werden.

An der Lösung des Randwertproblems mit Absorbing-Boundary-Bedingungen wird noch gearbeitet.

Die Ergebnisse der Forschungsarbeiten wurden in den Publikationen [3-7] dargestellt.

Projektliteratur:

K. BEILENHOFF, W. HEINRICH, H. L. HARTNAGEL, Improved finite-difference formulation in frequency domain for three-dimensional scattering problems, IEEE Transactions on Microwave Theory and Techniques, 40 (1992), No. 3, pp. 540-546.
A. CHRIST, H. L. HARTNAGEL, Three-dimensional finite-difference method for the analysis of microwave-device embedding, IEEE Transactions on Microwave Theory and Techniques, MTT-35 (1987), No. 8, pp. 688-696.
G. HEBERMEHL, R. SCHLUNDT, H. ZSCHEILE, W. HEINRICH, Improved numerical methods for the simulation of microwave circuits, erscheint in: Surveys on Math. Indust.
$\dito$ , Computation of eigen modes for transmission lines, in: Report of the Workshop Scientific Computing in Electrical Engineering (P. Deuflhard, H. Gajewski, G. Hebermehl, W. Heinrich, A. Kost, U. Langer, T. Weiland, Hrsg.), WIAS-Report No. 16, Berlin, 1998, pp. 34-35.
$\dito$ , Numerical solution of the eigenmode problem for microwave transmission lines, in: Proceedings of the Fourth International Conference on Mathematical and Numerical Aspects of Wave Propagation (John A. DeSanto, Hrsg.), Golden, Colorado, USA, SIAM, Philadelphia, 1998, pp. 606-608.
$\dito$ , Improved numerical methods for the simulation of microwave circuits, WIAS-Preprint No. 467, 1998.
R. SCHLUNDT, G. HEBERMEHL, H. ZSCHEILE, W. HEINRICH, On the computation of systems of linear algebraic equations for monolithic microwave integrated circuits, in: Report of the Workshop Scientific Computing in Electrical Engineering (P. Deuflhard, H. Gajewski, G. Hebermehl, W. Heinrich, A. Kost, U. Langer, T. Weiland, Hrsg.), WIAS-Report No. 16, Berlin, 1998, p. 40.

**Abb. 1:** Durchkontaktierung, Feldlinien einer Mikrostreifen-Mode
$\ProjektEPSbildNocap {0.65\textwidth}{field_beh_2.eps}$