Concrete application examples based on adaptive mesh generation methods
Frederic Alauzet
INRIA Roquencourt, France
Abstract:

A series of concrete, presumably impressive, application examples are presented which make use of adaptive processes coupling mesh adaptation and metric issues related to error estimates.

Then mesh generation methods together with metric construction and use are discussed.

Appropriate geometries and grids for anisotropic layered domains in applications of PDEs
Dirk Feuchter
Universität Heidelberg, Germany
Abstract:

Suitable geometries and grids are an important assumption of the numerical simulation of partial differential equations [1].

Considering drug diffusion through human skin, the main barrier is the stratum corneum with its layers of elongated flattened corneocytes embedded in a strongly anisotropic lipid matrix [2]. Also geoscientific simulations such as ground water migration or density driven flow must be realized for stratigraphic sequences mostly consisting of highly anisotropic layers [3].For such geometries with exhibiting extensions in a certain direction we are particularly engaged in the generation of appropriate geometries and preferably good grids [4], [5]. But how shoud a good grid element look like?

Generally, mesh generation for such anisotropic domains result in grid elements, which are anisotropic as well and should be suitable for an anisotropic refinement. We show several ways in order to describe the anisotropy of such grid elements.

After that we deal with the modeling of geometries for stratigraphic sequences. Using geostatistical methods on given bore hole data result in parting surfaces between layers. Using the thickness of layers avoids intersections and leads to consistent domains. Using a grid generation approch with vertical edges for such anisotropic (in horizontal direction) domains result in hybrid grids consisting of pyramids, tetrahedra, prisms and mainly hexahedra with no element angles near 180°. We present grids for several practical examples (island in the th Sea, layered domain above a saltdome in German Lowlands, groundwater basin in California). The geometry- and meshfiles are available to our simulation software UG.

Then we present our approch to geometry- and grid generation for the stratum corneum. We give several reasons that the shape of a single corneocyte is very similar to a tetrakaidecahedron. It is possible to assemble tetrakaidecahedra one upon the other and side by side without gaps in a densest packing and with minimal area for all required interfaces. With our approach geometric characteristics such as diameter, height, shape and angles of the corneocytes as well as the thickness of the lipid channels can be choosen arbitrarily. Furthermore, we are able to control the shift of composed corneocytes and our concept allows to assemble many corneocytes in rows, columns and layers all embedded in a lipid matrix [5]. We present a hybrid decomposition of our tetrakaidecahedra based geometry consisting of hexahedra, prisms, pyramids and tetrahedra [6] . The created geometries and grids can be used for the numerical simulation of drug diffusion [7].

The questions, whether the shown grids are optimal for the applications of partial differential equations and how a good grid element shoud look like in general, remain open and may inspire to discuss [8].

References

[1] Bastian P., Birken K., Johannsen K., Lang S., Reichenberger V., Wieners C., Wittum G., Wrobel C.: A parallel software-platform for solving problems of partial differential equations, in: High performance computing in science and engineering, Krause E., Jäger W. (eds.), Springer pp 326-339 (1999).

[2] Heisig, M., Lieckfeldt, R., Wittum, G., Mazurkevich, G., Lee, G.: Non-Steady-state Descriptions of Drug Permeation Through Stratum Corneum. I. The Biphasic Brick-and-Mortar Model. Pharm. Res. 13, 421-426 (1996).

[3] Johannsen K.: Numerical Aspects of Density Driven Flow in Porous Media (in German), K. Johannsen, Professorial Dissertation (Habilitation), University of Heidelberg

[4] Feuchter D., Stemmermann U., Wittum G: Description and generation of geometries and grids for layered domains, 17th GAMM Seminar Leipzig on Construction of Grid Generation Algorithms, http://www.mis.mpg.de/conferences/gamm/2001/ , ISBN 3-00-007753-7, pp 29-54, 2001.

[5] Feuchter D., Heisig M., Wittum G.: A geometry model with tetrakaidecahedra for the simulation of drug diffusion through the stratum corneum, Computing and Visualization in Science, Springer 2005, to appear

[6] Feuchter D., Heisig M., Liu Y., Wittum G.: Simulation der Arzneimitteldiffusion durch das Stratum Corneum - 1. Geometrie- und Gittererzeugung mit Tetrakaidekaedern, WiR Preprint 04/2004, Universität Heidelberg (in German).

[7] Heisig, M., Modeling and numerical simulation of drug diffusion through stratum corneum Third M.I.T Conference on Computational Fluid and Solid Mechanics, Special Session Localized Drug Delivery, June 14 - 17, 2005 at the Massachusetts Institute of Technology Cambridge, MA 02139 U.S.A.

[8] Shewchuk J. R.: What is a good linear Finite Element? Interpolation, Conditioning, Anisotropy, and Quality Measures (Preprint) http://www.cs.cmu.edu/~jrs/jrspapers.html

From quality and robustness issues in pure Delaunay algorithms to Delaunay based algorithms and anisotropic mesh construction
Paul Louis George
INRIA Roquencourt, France Abtract:

At first we give some controversial ideas about some commonly admitted things about Delaunay triangulations and meshes.

Then computer implementation concerns lead us to discuss robustness issues.

As a consequence, different ways of thinking the mesh generation problem are presented leading to interesting and actual extensions such as anisotropic meshing and mesh adaptation.

Parallel Implementation of a Dynamic Unstructured

Chimera Method

Aziz Madrane¹

¹ E-mail: aziz.madrane@airbus.com

Abstract:

Aerodynamic problems involving moving geometries have many applications, including store separation, high-speed train entering into a tunnel, simulation of full configurations of the helicopter and fast maneuvrability. Chimera method [1] offers the option of calculating these procedures. The solution process uses a grid system that discretizes the problem domain by using separately generated but overlapping unstructured grids that update and exchange boundary information through interpolation. However, such computations are complicated and time consuming [2]. Parallel computing offers a very effective way to improve the productivity in doing computational fluid dynamics (CFD). Therefore the purpose of this study is to develop an efficient parallel computation algorithm for analyzing the flowfield of complex geometries using overset grid technique. The strategy adopted in the parallelization of the overset grids method including the use of hierarchical data structures and communication, will be described.Numerical results are presented to demonstrate the efficiency of the resulting parallel overset grid method.

(a) Intergrid boundary

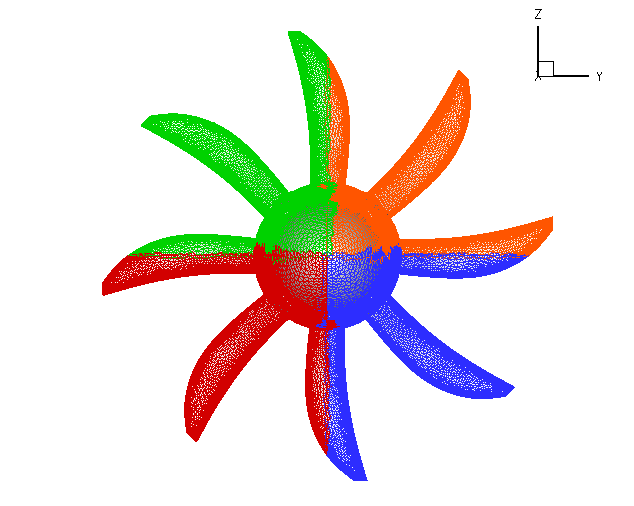
(b) Four partitions of an isolated propeller

Figure 1. Isolated propeller geometry

References:

[1] Steger, J.L. and Benek, J.A., On the Use of Composite Grid Schemes in Computational Aerodynamics, Computer Methods in Applied Mech. and Engeneering, 64, 301-320, (1987)

[2] Madrane, A., Heinrich R. and Gerhold T., Implemetation of the Chimera method in the unstructured hybrid DLR finite volume Tau-Code. 6^th Overset Composite Grid and Solution Technology Symposuim. Ft.Walton Beach, Florida, USA, October 8-10, 2002. http://www.arl.hpc.mil/Overset2002/

[3] A.Madrane, Parallel Implementation of a Dynamic Overset Unstructured Grid Approach.

ECCOMAS2004, Jyvaskyla, Finland on 24-28 july 2004.

http://www.mit.jyu.fi/eccomas2004/

[4] F. Brezzi, J.L. Lions, O. Pironneau, Analysis of Chimera Method, C.R. Acad. Sci. Paris, t.332, Serie 1, pp. 655-660, 2001.

Current Status of TetGen
Hang Si
WIAS, Berlin, Germany
Abstract:

TetGen is a 3D quality Delaunay mesh generator. The tetrahedral meshes are suitable for finite element and finite volume methods. The implemented Delaunay mesh algorithms are state-of-the-art and theoretically provable. It is a practical useful tool to combine research and applications.

This talk discusses the mesh problems it solves and the Delaunay mesh algorithms utilized in it. Some open issues are addressed. A future plan is provided for discussion.

Star Splaying: An Algorithm for Repairing Nearly-Delaunay Triangulations
Jonathan Richard Shewchuk
University of California, Berkeley, USA
Abstract:

The finite element method is popular in scientific simulation and computer animation as a way to model physical phenomena, and Delaunay triangulations are popular as geometric models of object and domains to be simulated. An ambitious goal is to simulate objects using moving meshes that track the shape of an object undergoing large deformations. The least understood part of this is what I call the "Delaunay repair problem": suppose the vertices of a Delaunay mesh have moved in response to physical forces, and the mesh is no longer Delaunay. Can we recover the Delaunay triangulation of the new vertex configuration faster than reconstructing the triangulation from scratch?

In two dimensions, the answer is yes. In 1977, Charles Lawson showed that any planar triangulation of a vertex set can be transformed into the Delaunay triangulation of the same vertices by a sequence of edge flips. The edge flips can be chosen by a simple hill-climbing algorithm.

In three or more dimensions, the notion of an edge flip generalizes to "bistellar flips," and the flip algorithm also generalizes, but the results do not. In practice, three-dimensional flipping gets stuck easily in local optima that are not Delaunay. In five-dimensional space, some triangulations cannot be transformed to Delaunay by any sequence of flips.

Thus I introduce star splaying, an algorithm that transforms any triangulation of any dimensionality into a Delaunay triangulation, and does so in a manner that is fast if few changes are needed. Star splaying has two main ideas. First, a triangulation is represented as a collection of "stars"--a star is the local neighborhood of each vertex. Second, the stars of two different vertices are not required to agree. Because star splaying permits temporary inconsistencies between stars, it can get past local optima that incapacitate the flip algorithm.

Combinatorics and Curvature of Tetrahedral Meshes

John M Sullivan
TU Berlin

Abstract:

In two dimensions, the Euler number gives a clear relationship between the combinatorics (average vertex valence) of a triangular mesh and the topology (or total curvature) of the meshed surface. For instance, for a planar domain with periodic boundary conditions, the average valence is exactly 6.

There is no analog in three dimensions, but there are still intriguing connections. The average edge valence can range exactly in the interval from 4.5 to 6. A new result (joint work with Frank Lutz) shows that any tetrahedral mesh (again with periodic boundary conditions) must have some edges of valence 6 or more.

Tighter relationships evidently arise when ome geometric control is placed on the shapes of tetrahedra. The TCP structures (from crystallography, but also observed in foam structures) are triangulations made from nearly-regular tetrahedra, with edge valences 5 or 6. Here the average valence is evidently always between 5.1 and 5.333, but this remains conjectural. TCP triangulations give examples of tetrahedral meshes with acute dihedral angles (joint work with Eppstein and Ungor). Unlike in 2D, acute triangulations in 3D are not necessarily Delaunay, but still should be high quality. It is an open problem to acutely triangulate the cube.