| |
U. Bandelow (Berlin):
Quantum-Classical Coupling in Multi Quantum Well Lasers |
The presence of quantum wells in laser diodes introduces a new length
scale, being in the order of the Fermi-wavelength of the carriers.
This induces a mixed spectral density, where the carriers localizing
within the quantum wells belong to the discrete spectrum and the
free-roaming carriers belong to the continuous spectrum.
Consequently, this divides the carriers into species which exhibit
different properties. In particular, the latter species is viewed
as a ''classical'' species, carrying classical transport on a large
scale (some 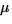 m).
By quantum well design the properties of the localized ''quantum''
species can be tuned and optimized for applications.
Due to their localized nature the above ''quantum'' species
cannot carry a current within a single-particle approach
and therefore acts as a null-space for the transport.
In consequence, their occupation remains fixed forever -
which is contradicting to physics. m).
By quantum well design the properties of the localized ''quantum''
species can be tuned and optimized for applications.
Due to their localized nature the above ''quantum'' species
cannot carry a current within a single-particle approach
and therefore acts as a null-space for the transport.
In consequence, their occupation remains fixed forever -
which is contradicting to physics.
Interaction as phonon-carrier and carrier-carrier scattering
will change this simplified picture and causes kinetical processes
for all the species. Among others, carriers can then migrate from
one species to another.
Above a certain time-scale such processes can be modeled in
some approximation in terms of a dynamics
which effectively counts the amount of carriers being captured by the
quantum wells as well as the amount of carriers escaping from the
quantum wells.
|
| |
M. Baro (Berlin):
Kirkner-Lent-Poisson system |
We analyse a Schrödinger-Poisson system on the interval
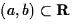 , i.e. the electrostatic potential , i.e. the electrostatic potential
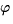 is determined by Poisson's equation is determined by Poisson's equation
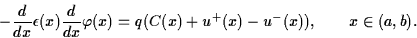
The densities 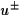 of electrons and holes are determined by
so-called Kirkner-Lent families of electrons and holes are determined by
so-called Kirkner-Lent families 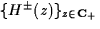 , i.e.
a family of Schrödinger-type operators , i.e.
a family of Schrödinger-type operators
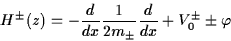
with
transparent boundary conditions
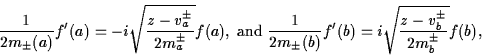
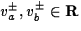 , , 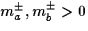 . .
This model allows to consider current carrying scattering states. Hence
a current coupling with a classical drift diffusion model is possible.
We will show that the Kirkner-Lent-Poisson system always admits
a solution and give some a priori estimates.
This is a joint work with P. Degond,
H.-Ch. Kaiser, H. Neidhardt, and J. Rehberg.
|
| |
C. Carstensen (Wien, AT):
Finite Element Approximation of Averaged Quantities in Microstructures |
|
This talk addresses a non-convex minimization problem
(M) motivated by variational models
(i) for phase transformations in crystal physics -advertised,
e.g., by Fonseca, Ball, James;
(ii) in optimal design tasks -advertised, e.g., by Kohn;
(iii) in micromagnetics -advertised, e.g., by Tartar.
In contrast to convex energy densities, a non-convex density W, typically,
leads to non-attainment of the infimal energy in (M) even though W is smooth
and satisfies proper growth conditions. The simplest 1D example
W(x)=(x2-1)2 due to Bolza serves as a basis to explain the lack of
sequentially weak lower semicontinuity and the enforced high
oscillations of infimizing sequences called microstructures.
The presentation illustrates those phenomena and their impact on a finite
element simulation (Mh): Strong convergence of gradients
is impossible! Essentially
two relaxation results from state-of-the-art calculus of variations are
available to cure the problem. Young measures and (quasi-) convexification
are the mathematical key concepts behind the proposed numerical
alternatives (Gh) and (Qh). Recent numerical algorithms and convergence
results form the center of the presentation. Mathematical difficulties
encountered in enforced microstructures
include non-quadratic growth conditions as well as a degenerated or even
non-convex relaxed energy functional. Comments on remedies to gain
strong convergence of gradients, open questions,
and future developments conclude the talk.
|
| |
M. Ehrhardt (Saarbrücken):
Discrete transparent boundary conditions for the Schrödinger equation: Fast calculation, approximation, and stability |
|
This talk is concerned with transparent boundary conditions (TBCs)
for the time-dependent Schrödinger equation in one and two dimensions.
Discrete TBCs are introduced in the numerical simulations of whole space
problems in order to reduce the computational domain to a finite region. Since
the discrete TBC for the Schrödinger equation includes a convolution
w.r.t.
time with a weakly decaying kernel, its numerical evaluation becomes very
costly for large-time simulations.
As a remedy we construct approximate TBCs with a kernel having the form of a
finite sum-of-exponentials, which can be evaluated in a very
efficient recursion. We prove stability of the resulting
initial-boundary value scheme, give error estimates for the considered
approximation of the boundary condition, and illustrate the
efficiency of the proposed method on several examples.
|
| |
G. Friesecke (Warwick, UK):
Long time dynamics of Fermi-Pasta-Ulam lattices: persistence of coherent modes and recurrence theorem for Fourier spectrum |
|
In joint work with R.L.Pego (Maryland), we have recently obtained
a recurrence theorem related to a fundamental question raised by Fermi,
Pasta
and Ulam in 1947.
F, P and U wondered numerically about the long time
behaviour of the Fourier spectrum of
a 1D nonlinear atomic chain with Hamiltonian
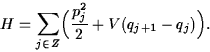
Statistical mechanics reasoning suggests that the nonlinearity would
promote asymptotically thermalized distribution of energy among the
Fourier
modes. (For a linear lattice, i.e. a quadratic potential V, the spectral
density would be time-independent).
But the numerical experiments showed
strong recurrence effects, which have remained poorly understood.
Our theorem says that given any energy surface H=E with sufficiently low
energy E, and given any 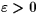 , there exists an open set of
initial
data whose Fourier spectral density is , there exists an open set of
initial
data whose Fourier spectral density is 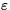 -recurrent. This means
that after each integer multiple of some recurrence time T, the spectral
density has distance at most -recurrent. This means
that after each integer multiple of some recurrence time T, the spectral
density has distance at most 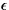 (in the L1 norm) from the
initial
density. (in the L1 norm) from the
initial
density.
Our construction of recurrent regions is related to the presence of
solitary wave modes in the lattice. (Much of the literature
has instead been viewing the FPU recurrences as KAM type effects.
But it seems it has not been possible
to turn this idea into a theorem. I will discuss an explanation suggested
by E.Wayne.)
|
| |
K. Gelfert (Dresden):
Langevin model for the slow motion in a deterministic multi-scale system |
|
In this talk we intend to establish a novel approach for the modelling
and effective simulation of systems with time-scale separation. For a
class of deterministic dynamical systems where the state space variables
can be divided into a group of fast and a group of slow variables it
will be discussed how a fast chaotic motion can be modelled by suitable
stochastic forces. Here, projection techniques, which are well known
from non-equilibrium statistical mechanics, are employed to eliminate
the fast motion. After an approximation step a Fokker-Planck equation
governing the evolution of the density of the slow variables is derived.
In this equation the diffusion term is given in terms of correlation
properties of the fast motion while the drift term consists of an
adiabatic average of the slow motion plus a renormalization by chaotic
fluctuations.
|
| |
J. Giannoulis (Stuttgart):
Young-measure solutions to a generalized Benjamin-Bona-Mahony equation |
|
We are interested in the evolution of macroscopic properties of microscopic
structure.
Starting from the viewpoint that microstructure can be modelled by spatial
highly oscillatory initial data, in order to obtain its macroscopic
information one is tempted to use the limit achieved
as the (micro-)period tends to zero, i.e, to use Young measures.
Indeed, Young measures maintain the macroscopic properties of oscillations
(the simplest examples being the main value, the amplitude etc.), while
they fade out the microscopic information.
Since we want to describe the evolution of the macroscopic features of our
data, we have to derive a macroscopic evolution equation for Young measures
from the given (microscopic) equation, the latter describing the evolution of
the oscillations.
This programme will be outlined for the case of a generalization of the BBM
equation (an ``alternative'' to the KdV equation)
showing exemplarily the (also numerical) advantages of the application of
such an approach.
|
| |
S. Goedecker (Grenoble, FR):
Wavelets, Plane Waves and Multigrid Methods in the Context of Poisson's Equation |
|
Wavelets, plane waves and multigrid methods share many central ideas.
An unified point of view can help us in the construction of more
efficient algorithms. In particular it will be shown how Poisson's
equation discretized in a wavelet basis can be solved efficiently in
a multigrid way and how multigrid algorithms can be improved by
incorporating wavelet concepts.
|
| |
M. Herrmann (Berlin):
Micro-macro transitions in the atomic chain |
|
In this talk we consider micro-macro transitions in an atomic chain
whose microscopic dynamics is described by a large system of
Newton equations with a nonlinear but convex interaction potential.
Starting form the hyperbolic scaling of space and time we discuss the
thermodynamical (macroscopic) describtion of the chain
for a suitable class of microscopic initial data. In particular,
we identify a closure principle that describes the statistical
distribution of the atoms for any macroscopic space time
point. Using this closure principle we can describe the macroscopic
behaviour of the chain by a system of hyperbolic pde's, namely
the well known Euler system of thermodynamics. Finally, we
study Riemann problems for the atomic chain.
|
| |
A. Jüngel (Konstanz):
Macroscopic semiconductor modeling and simulation |
|
The ongoing miniaturization of semiconductor devices reached
nowadays a length scale at which quantum effects play a dominant
role. Therefore, standard models like the classical drift-diffusion
equations are physically inaccurate and have to be replaced by
models which incorporate the relevant quantum effects. The state
of the art in quantum semiconductor modeling ranges from microscopic
models, like Schrödinger or Wigner equations, to macroscopic
equations, like quantum hydrodynamic models.
This talk gives an overview of various macroscopic quantum
models and presents analytical and numerical results on some of
these models, in particular the (1) quantum drift-diffusion,
(2) quantum hydrodynamic, and (3) viscous quantum hydrodynamic
equations.
|
| |
K. Kirchgässner (Stuttgart):
Travelling waves in a chain of coupled nonlinear oscillators |
|
In a chain of nonlinear oscillators, linearly coupled to their nearest
neighbors, all travelling waves of small amplitude are found as
solutions of finite dimensional reversible dynamical systems. The
coupling constant and the inverse wave speed form the parameter space.
The ground state consists of a one-parameter family of periodic waves.
It is realized in a certain parameter region containing all cases of
light coupling. Beyond the border of this region the complexity of
wave-forms increases via a succesion of bifurcations. An appropriate
fomulation of this problem will be given, and the basic facts about
the reduction to finite dimensionional systems will be indicated. We
show the existence of the ground state and discuss the first
bifurcation via normal form arguments. Furthermore we show the
existence of nanopterons, i.e. localized waves with noncancelling
periodic tails at infinity which are exponentially small in the
bifurcation parameter. (Joint work with G.Iooss, CMP 211(2000)).
|
| |
C. Lasser (München):
Molecular dynamics and energy level crossings |
|
The Born-Oppenheimer approximation to quantum-mechanical molecular
dynamics locally breaks down in the presence of energy level crossings.
There are various types of energy level crossings, each of it associated
with an own Landau-Zener formula.
An asymptotic analysis of a Schrödinger equation with level crossing can
be carried out by taking the solution's Wigner transform and passing to
the semiclassical limit; an approach, which has been introduced to this
problem class by C. Fermanian and P. Gérard.
We will adopt this point of view and discuss some simple model problems
with avoided crossing, codimension one and codimension two crossing.
|
| |
H. Luo (Kassel):
Wavelet approximation of correlated wavefunctions |
|
We suggest an alternative approach for the local treatment
of electron corelation based on numerical methods from
multiscale analysis. By this we are aming to achieve a better
description of the various length- and energy-scales inherently
connected with different types of electron correlations.
For the first step, we take the local ansatz which corresponds to
a coupled electron pair approximation (CEPA), and approximate
the correlation part by means of hyperbolic wavelets.
We perform diagramatic analysis for the calculation of the matrix
elements.
|
| |
K. Matthies (Berlin):
Atomic-scale localization of high-energy solitary waves on lattices |
One-dimensional monatomic lattices with Hamiltonian
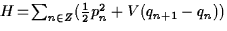 are known to
carry localized travelling
wave solutions, for generic
nonlinear potentials V. In this talk we derive the
asymptotic profile of these waves
in the high-energy limit are known to
carry localized travelling
wave solutions, for generic
nonlinear potentials V. In this talk we derive the
asymptotic profile of these waves
in the high-energy limit 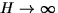 , for Lennard-Jones type
interactions.
The limit profile is proved to be a universal, highly discrete, piecewise
linear wave concentrated on a single atomic spacing.
This shows that dispersionless energy transport in these systems is not
confined to the long-wave regime. (Joint work with G. Friesecke, Physica
D, to appear) , for Lennard-Jones type
interactions.
The limit profile is proved to be a universal, highly discrete, piecewise
linear wave concentrated on a single atomic spacing.
This shows that dispersionless energy transport in these systems is not
confined to the long-wave regime. (Joint work with G. Friesecke, Physica
D, to appear)
|
| |
F. Mehats (Tolouse, FR):
Analysis of a Drift-Diffusion-Schrödinger-Poisson model |
|
(joint work with N. Ben Abdallah and N. Vauchelet)
We present the analysis of a coupled quantum-classical system,
modeling the transport of a quasi bidimensional electron gas
confined in a
nanostructure. The coupling occurs in the momentum variable: the
electrons are like point particles in the directions x parallel to
the gas (classical transport)
while they behave like waves in the transversal direction
z (quantum description).
The transport of the gas is described by a 2D Drift-Diffusion equation,
governing the evolution of a surfacic density ns.
The originality of this system is that the parameters of this
equation keep a trace of the quantum confinement in the
transversal direction. Indeed, the effective potential which gives the
drift current is calculated with the subband model
through the resolution of an adiabatic
Schrödinger-Poisson system. It takes into account the
selfconsistent electric potential generated by the electrons and the
quantification of the energy in the z variable. The system can be obtained, at least formally, as the
diffusion limit of a Boltzmann-Schrödinger-Poisson system.
Let 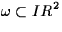 be a regular and bounded domain and let be a regular and bounded domain and let
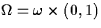 . The spatial variables are . The spatial variables are
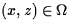 .The model studied here is the following coupled system: .The model studied here is the following coupled system:
| 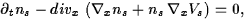 |
(1) |
| 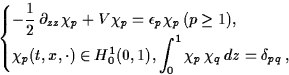 |
(2) |
| 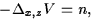 |
(3) |
where the unknowns are the surfacic density ns(t,x),
the eigen-energies 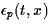 ,
the eigenfunctions ,
the eigenfunctions 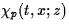 ,and the electrostatic potential V(t,x,z).
These equations are coupled through the density n and the effective
potential Vs, which are defined by ,and the electrostatic potential V(t,x,z).
These equations are coupled through the density n and the effective
potential Vs, which are defined by
| 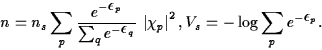 |
(4) |
This system (1)-(4) is completed with
an initial condition and conservative boundary conditions.
Using a fixed-point procedure,
we have proved the existence of a unique solution to this
nonlinear system.
|
| |
J. M. Melenk (Leipzig):
Generalized FEM and two-scale regularity for homogenization problems |
|
We present regularity results for the solutions
of a class of elliptic boundary value problems with rapidly
oscillating, periodic coefficients. At the heart
is a detailed analysis of the so-called unit-cell
problem. Applications of our results include mesh design
principles for the generalized FEM (gFEM).
The gFEM introduced by A.-M. Matache and C. Schwab
is a projection method with problem-adapted ansatz space
that can lead to robust convergence, i.e., the convergence is
independent of the coefficients' period. In this talk, we will
review the gFEM and elaborate the bearing of our regularity
results on it.
|
| |
A. Mielke (Stuttgart):
Macroscopic dispersive energy transport in harmonic lattices |
|
We study oscillations of an infinite periodic
lattice in one or several space dimensions. We consider the atomic distance
1/n as
the small microscopic length scale and the aim is to derive macroscopic
evolution laws. The simplest model displaying already most features is the
one-dimensional chain
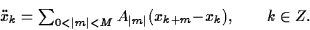
From the microscopic dispersion relation
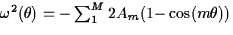 we have the exact solutions we have the exact solutions 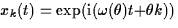 . Using Fourier transform yields the general
solutions. . Using Fourier transform yields the general
solutions.
Defining the macroscopic functions 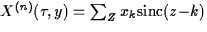 , with sinc , with sinc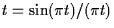 ,in the macroscopic variables ,in the macroscopic variables 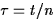 and y=z/n
we obtain via weak convergence arguments that the associated macroscopic limit
equation is the linear wave equation and y=z/n
we obtain via weak convergence arguments that the associated macroscopic limit
equation is the linear wave equation
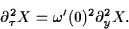
The microscopic energy distribution distribution is a quadratic functional of
the vleocities and the strains. It is shown that the Wigner transform can be
used to describe its weak limit. The associated limit for 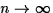 is a measure
is a measure 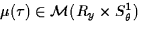 which has to satisfy the transport equation which has to satisfy the transport equation
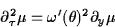
in the sense of distributions.
|
| |
H. Neidhardt (Berlin):
Current coupling of drift -diffusion and Schrödinger-Poisson systems |
|
(joint work with M.Baro, H.-Chr.Kaiser,and J.Rehberg)
Let ![$\hat{{\Omega}} = [a_0,b_0]$](ab_neidhardt_img1.gif) be an closed interval on
the real axis which contains the closed interval be an closed interval on
the real axis which contains the closed interval
![${\Omega}= [a,b] \subset \hat{{\Omega}}$](ab_neidhardt_img2.gif) .
On the semi-intervals .
On the semi-intervals
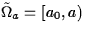 and and ![$\tilde{{\Omega}}_b = (b,b_0]$](ab_neidhardt_img4.gif) ,
which are called classical zones, one-dimensional
drift-diffusion models without generation and recombination are
considered while on the closed interval ,
which are called classical zones, one-dimensional
drift-diffusion models without generation and recombination are
considered while on the closed interval 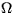 ,
which is called the quantum
zone, a description by dissipative Schrödinger-Poisson systems with
given densities matrices (steady states) is assumed.
Both systems are coupled to a hybrid
model as follows: ,
which is called the quantum
zone, a description by dissipative Schrödinger-Poisson systems with
given densities matrices (steady states) is assumed.
Both systems are coupled to a hybrid
model as follows:
- 1.
- The boundary coefficients of the dissipative Schrödinger-Poisson
systems are determined by the quasi-Fermi levels of the drift-diffusion
models in accordance with dissipative Kirkner-Lent models, see talk of
M. Baro.
- 2.
- The current densities are constant for the coupled system, in
particular, current densities for the classical and
quantum zones are equal (current coupling).
It is shown that under these assumptions the hybrid model has always
a solution which is in general not unique.
|
| |
R. Schneider (Chemnitz):
Wavelet subspace splitting |
|
Wavelet compression is a favourable tool
for an efficient approximation of singularities.
Moreover the hierarchical description admits a hyperbolic cross
or sparse grid approximation, reducing the complexity of
multidimensional problems. Both can be used for
the numerical ab initio solution of many particle Schrödinger
equation.
Even Kato type singularies are resolved adaptively.
However these results are limited and not satisfactory.
At this point it becomes necessary to go beyond classical
wavelet analysis.
The complexity is too high, because the information
encoded by the wavelet bases is still redundant.
The idea to overcome this deficiency is to split
the wavelet spaces itself into several
subspaces where only a low dimensional
subspace contains the essential information.
This may be viewed as a better and more appropriate
localization in the frequency domain.
In fact, we are constructiong wavelet
subspaces with higher order vanishing moments
by linear combination of wavelet functions.
The resulting basis functions are builting again Riesz bases.
We
show how to apply this construction to resolve Kato type singularities.
At the end we apply the present concept to construct
a stable wavelet methods which is exponetially convergent for analytic datas.
By the introduction of new basis functions we have enriched our libary
of basis functions. A best N-term approximation becomes now a
problem of finding best bases.
The strategy to find this bases depends on which a priory information
is available.
|
| |
S. Teufel (München):
Effective dynamics in a periodic potential: Peierls substitution and beyond |
|
The dynamics of electrons in a crystal can be described
in good approximation by the Schrödinger equation for a single particle
with a periodic potential.
Typically external magnetic and electric fields are weak compared to the
periodic field and thus
the external potentials have a slow variation on the scale set by the lattice.
As a consequence of this separation of scales the macroscopic dynamics of
the electron
are governed by an effective Hamiltonian obtained through the famous
``Peierls substitution''.
We present a perturbative scheme which allows not only for a rigorous
justification for
``Peierls substitution'', but also yields corrections to arbitrary
order in the
small parameter describing the separation of scales.
|
| |
F. Theil (Warwick, UK):
Surface energies in lattice models |
Probably the best known finite scale effects in atomistic systems are
surface energies. In a simplistic, two-dimensional model the total
energy E associated to the atom positions 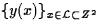 is given by the pair sum is given by the pair sum
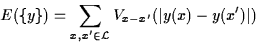
where the potential Vx-x' is harmonic if ![$\vert x-x'\vert \in
[1,\sqrt{2}]$](ab_theil_img3.gif) and 0 else.
This corresponds to a system of mass points coupled via linearly
elastic springs. For and 0 else.
This corresponds to a system of mass points coupled via linearly
elastic springs. For 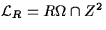 where R>0 is a scaling
parameter and
where R>0 is a scaling
parameter and 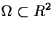 is a a continuum domain the
minimum energy scales in the following way is a a continuum domain the
minimum energy scales in the following way
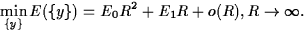
The surface term
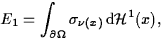
where 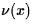 is the surface normal at x, encodes information about
the relaxation pattern of the atoms close to the surface. We show that
in many cases is the surface normal at x, encodes information about
the relaxation pattern of the atoms close to the surface. We show that
in many cases 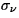 can be found by solving 1-periodic cell
problems. The result can be described as a Cauchy-Born rule for
surfaces. can be found by solving 1-periodic cell
problems. The result can be described as a Cauchy-Born rule for
surfaces.
When the surface relaxation is ignored, 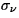 depends smoothly
on the normal vector depends smoothly
on the normal vector 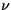 except on a closed set of measure 0. The
nontrivial relaxation pattern of the atom positions towards the
interiour changes the qualitative behaviour of except on a closed set of measure 0. The
nontrivial relaxation pattern of the atom positions towards the
interiour changes the qualitative behaviour of 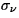 dramatically. Numerical studies indicate that even for small surface
relaxation dramatically. Numerical studies indicate that even for small surface
relaxation 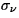 might be nowhere smooth in might be nowhere smooth in 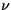 . .
|
![]()
![]()
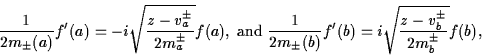
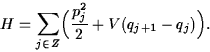
![]() , there exists an open set of
initial
data whose Fourier spectral density is
, there exists an open set of
initial
data whose Fourier spectral density is ![]() -recurrent. This means
that after each integer multiple of some recurrence time T, the spectral
density has distance at most
-recurrent. This means
that after each integer multiple of some recurrence time T, the spectral
density has distance at most ![]() (in the L1 norm) from the
initial
density.
(in the L1 norm) from the
initial
density.
![]() be a regular and bounded domain and let
be a regular and bounded domain and let
![]() . The spatial variables are
. The spatial variables are
![]() .The model studied here is the following coupled system:
.The model studied here is the following coupled system:
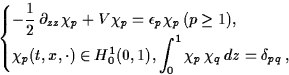
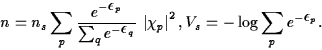
![]()
![]() , with sinc
, with sinc![]() ,in the macroscopic variables
,in the macroscopic variables ![]() and y=z/n
we obtain via weak convergence arguments that the associated macroscopic limit
equation is the linear wave equation
and y=z/n
we obtain via weak convergence arguments that the associated macroscopic limit
equation is the linear wave equation
![]()
![]()
![]() be an closed interval on
the real axis which contains the closed interval
be an closed interval on
the real axis which contains the closed interval
![]() .
On the semi-intervals
.
On the semi-intervals
![]() and
and ![]() ,
which are called classical zones, one-dimensional
drift-diffusion models without generation and recombination are
considered while on the closed interval
,
which are called classical zones, one-dimensional
drift-diffusion models without generation and recombination are
considered while on the closed interval ![]() ,
which is called the quantum
zone, a description by dissipative Schrödinger-Poisson systems with
given densities matrices (steady states) is assumed.
Both systems are coupled to a hybrid
model as follows:
,
which is called the quantum
zone, a description by dissipative Schrödinger-Poisson systems with
given densities matrices (steady states) is assumed.
Both systems are coupled to a hybrid
model as follows:
![]()
![]()
![]()
![]() depends smoothly
on the normal vector
depends smoothly
on the normal vector ![]() except on a closed set of measure 0. The
nontrivial relaxation pattern of the atom positions towards the
interiour changes the qualitative behaviour of
except on a closed set of measure 0. The
nontrivial relaxation pattern of the atom positions towards the
interiour changes the qualitative behaviour of ![]() dramatically. Numerical studies indicate that even for small surface
relaxation
dramatically. Numerical studies indicate that even for small surface
relaxation ![]() might be nowhere smooth in
might be nowhere smooth in ![]() .
.