
Matheon-C26
Storage of hydrogen in hydrides


|
Matheon-C26
|
 |
| Prof. Dr. Wolfgang Dreyer | |
| Thermodynamic Modeling and Analysis of Phase Transitions | |
| Weierstrass Institute for Applied Analysis and Stochastics, Mohrenstr. 39, 10117 Berlin, Germany | |
| Tel: +49 30 20372 537 | |
| email: dreyer{at}wias-berlin.de | |
| Members: | Clemens Guhlke |
| Collaboration: |

|
Hydrogen is the ideal synthetic fuel to convert chemical energy into electrical energy or into motive power because it is light weight, highly abundant and its oxidation product is vapor of water. Thus its usage helps to reduce the greenhouse gases and it conserves fossil resources. There is even a clean way to produce hydrogen by electrolysis of water by means of photo voltaics.
There are various possibilities to store the hydrogen for later use: Liquid and gaseous hydrogen can be stored in a pressure vessel, hydrogen can be adsorped on large surface areas of solids, and finally crystal lattices of metals or other compounds can be used as the storage system, where hydrogen is dissolved either on interstitial or on regular lattice sites. The latter process and its reversal is called hydriding respectively dehydriding. The subject of this proposal is the modelling and simulation of that process.
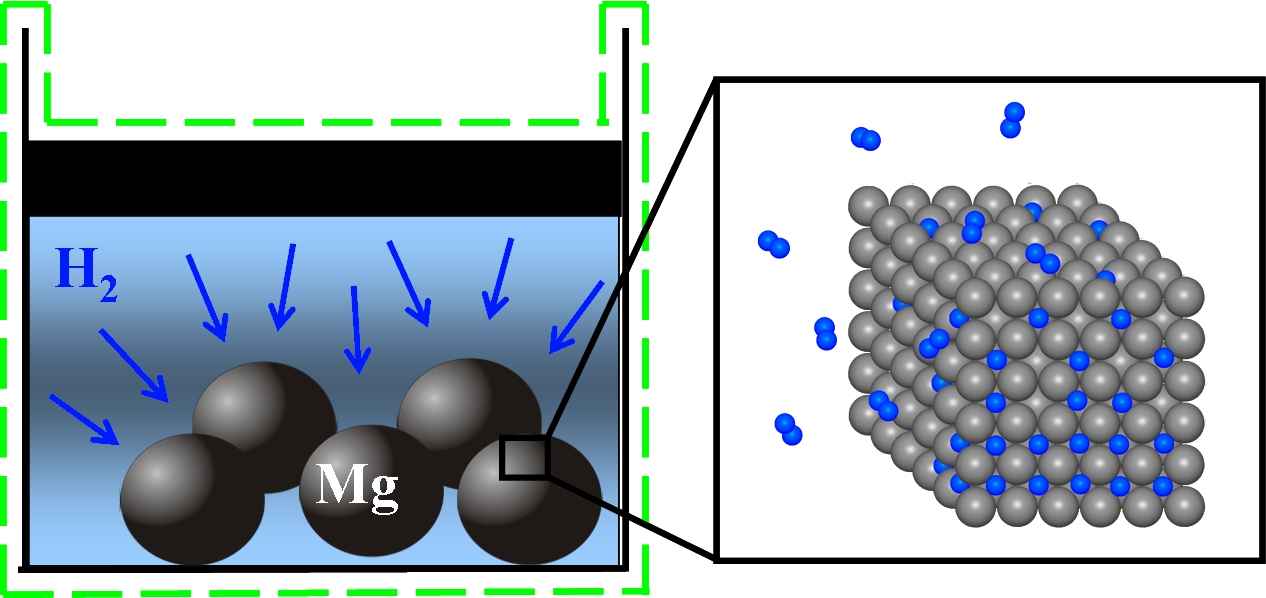
Figure 1: Illustration of the hydriding process of an ensemble of many magnesium storage particles
The storage processes is accompanied by a phase transition and by hysteretic behavior during loading and unloading. Hydrogen storage in metals is characterized by the relation between the hydrogen vapor pressure of the device and the total amount of stored hydrogen.
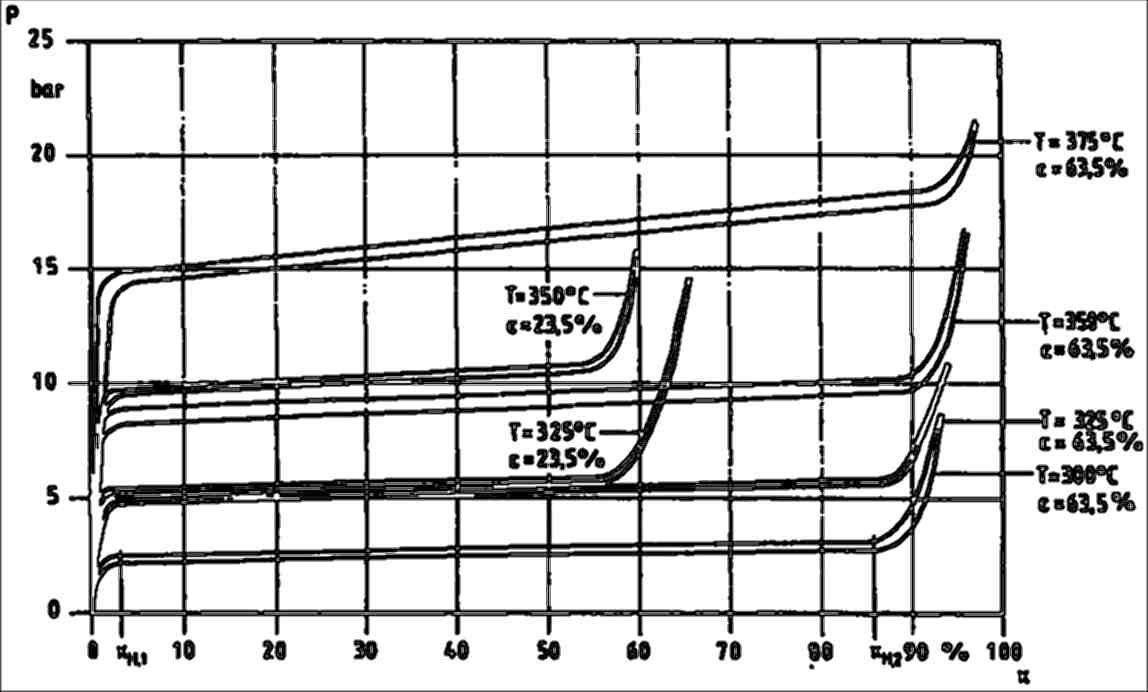
Figure 2: Hydrogen vapor pressure versus hydrogen content per lattice site of Mg. [W.Klose and V.Stuke, Chem.-Ing.-Tech. 64 (1992) Nr. 4, p. 360-361]
We have chosen the storage substance magnesium (Mg) as the simplest demonstrator to establish a model for reversible hydrogen storage. Its chemical and mechanical properties are already well understood and Mg can most effectively absorb hydrogen. The storage system consists of a fine powder of magnesium particles of diameter in the 0.1μm range. The model for hydrogen storage relies on a corresponding model that the applicant has established for lithium-ion batteries, [DGGHJ11]. The sharp interface version of the model consists of a parabolic/elliptic system of PDEs with generalized Stefan conditions, the Young-Laplace law and kinetic relations at the sharp interfaces between two coexistent phases that appear in the course of lithium storage as well as during hydrogen storage. It is important to note that the Mg crystal elastically changes its volume by 30% during loading. Thus the use of nonlinear elasticity theory is mandatory.
| Conservation equation | Jump conditions | Kinetic relations at the Interface | ||
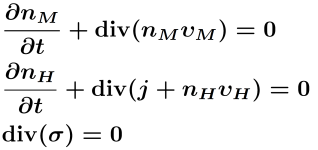
|
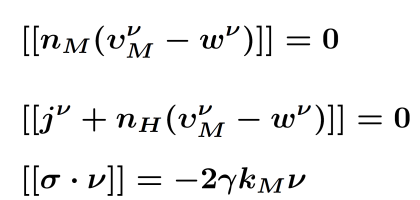
|
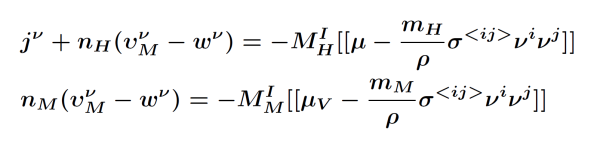
|
In order to determine the onset of the two-phase region, a phase field model is needed, whose sharp interface limit leads to the above setting. However, currently there is no phase field model available that is capable to give both kinetic relations. For this reason we exploit by formal asymptotic expansions four possible candidates and arrive at two conclusions:
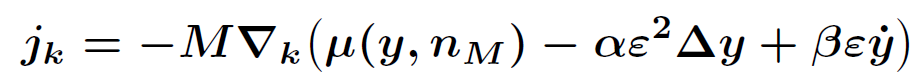
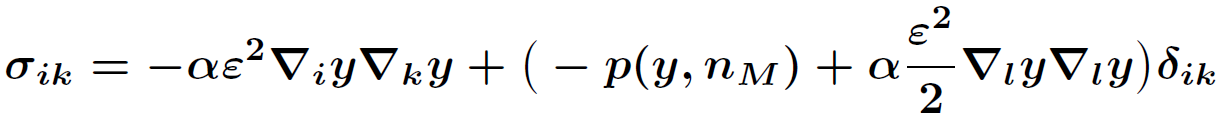 .
.
There is an apparent paradox concerning the storage problem. The observed hysteretic behavior of the loading-unloading process can be understood by a phase transition that happens in a single storage particle. However, if the particle size is below a critical value, the phase transition in the single particle disappears but the observed hysteresis remains. We could resolve the paradox and show that the hysteresis may be induced either by a phase transition in a single storage particle or by a cooperative effect of the powder consisting of many particles. In the latter case no phase transition in the single particle is necessary. This prediction is confirmed by experiments.
The free energy of the N storage particle system can be written in the form
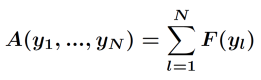 .
.
For quasi-static loading and unloading, the storage system evolves via the minimizers of the free energy under the side condition
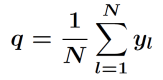 .
.
|
|
|
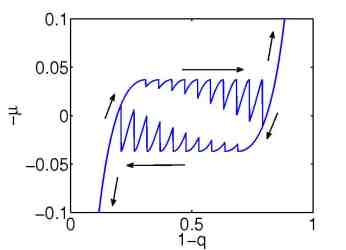
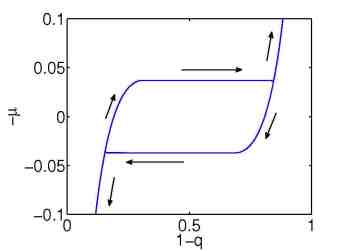
| Figure 3: Simulation of an loading/unloading process with a many particle model. Left: 10 particles. Right: 1000 particles. | ||
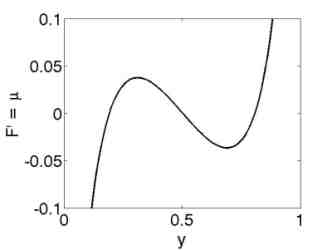
The quasi-static model explains the origin of the hysteresis as a many particle effect, where the chemical potential of a single storage particle is given by a non-monotone function of the concentration y, see Figure 4.
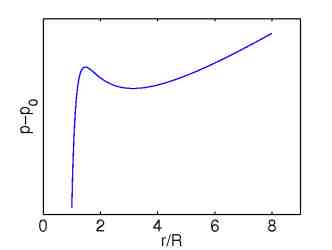
A system of interconnected rubber balloons exhibits similar behavior as the system of many storage particles, because the pressure-radius characteristic of a single balloon shows likewise non-monotone behavior, compare Figures 4 and 5.
|
|
|
| Figure 4: Non-monotone chemical potential. | Figure 5: Pressure radius characteristic of a rubber balloon. |
If we constantly supply air via the pressure vessel to 24 interconnected balloons, see Figure 6, we observe the following: For small filling the balloons are small and have the same size until they reach the end of the first increasing pressure-radius branch, see Figure 5. Here the experiment shows that only one balloon will quickly pass through the decreasing branch to an apparently larger radius. In that time the other balloons slightly decrease, and in this time regime we thus have one large balloon and N-1 small ones. The regime ends when the small balloons again reach the end of the first increasing pressure-radius branch. One further balloon passes to a larger radius and for a while we have now a state with 2 large balloons and N-2 small ones. This process is repeated until all balloons have the same large size, which is the last state of the sequence from Figure 6.

|

|

|

|
| Figure 6: Four different states of connected rubber balloons during loading with air via the pressure vessel. | |||
|
|
|
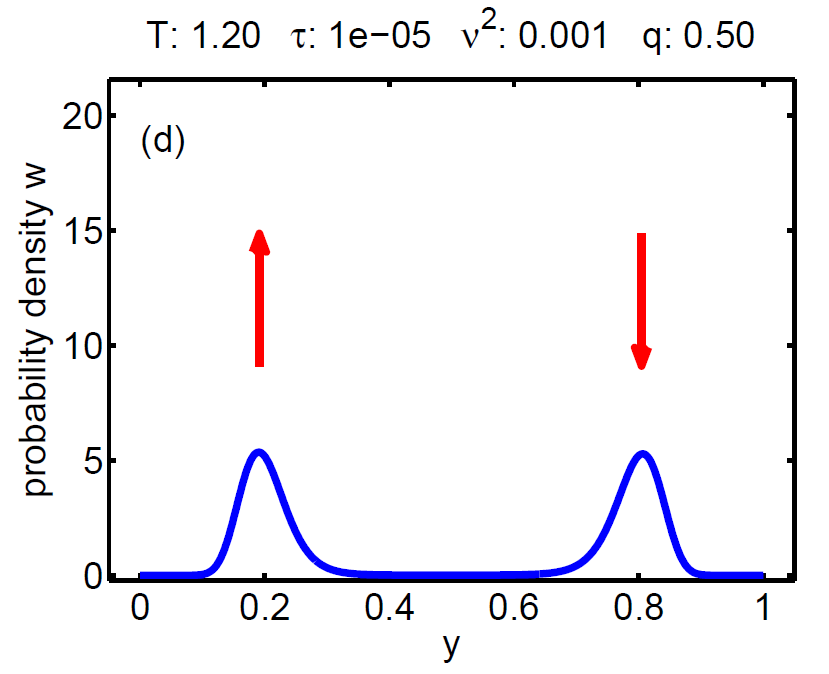
|
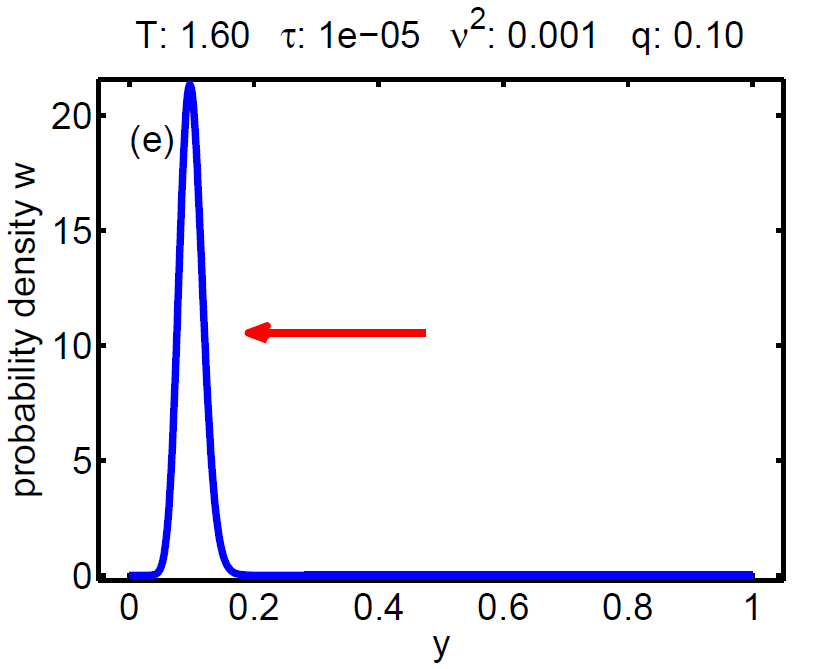
|
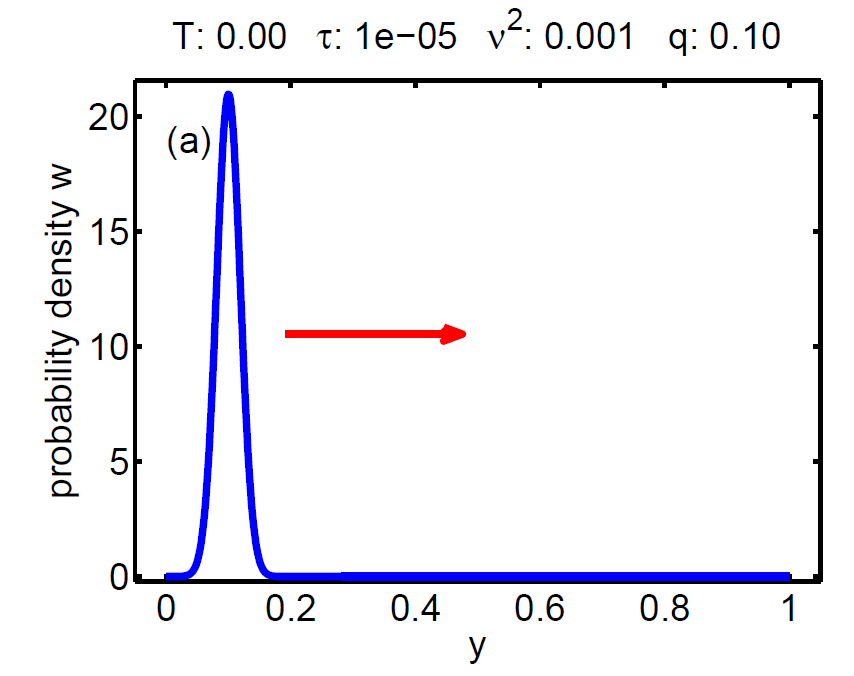
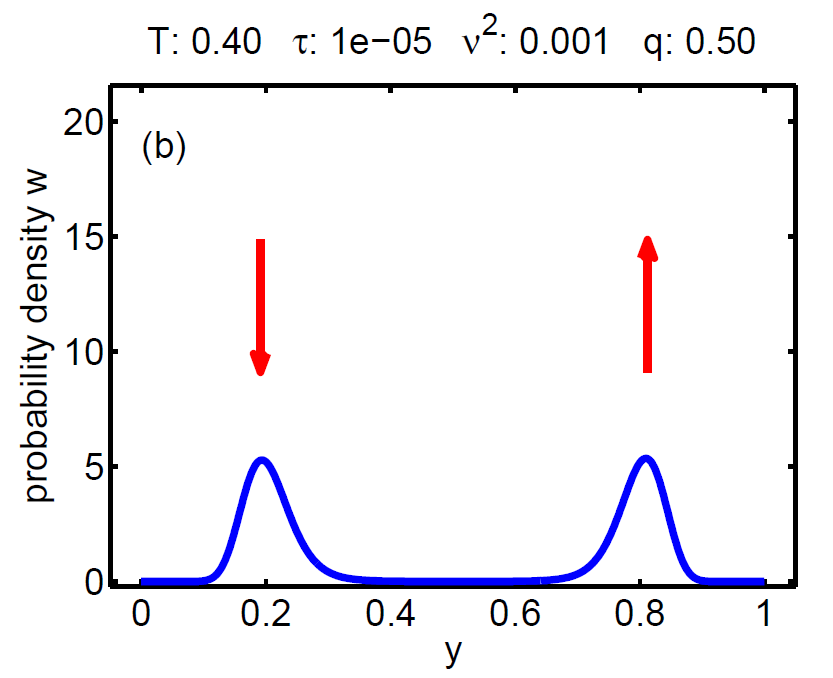
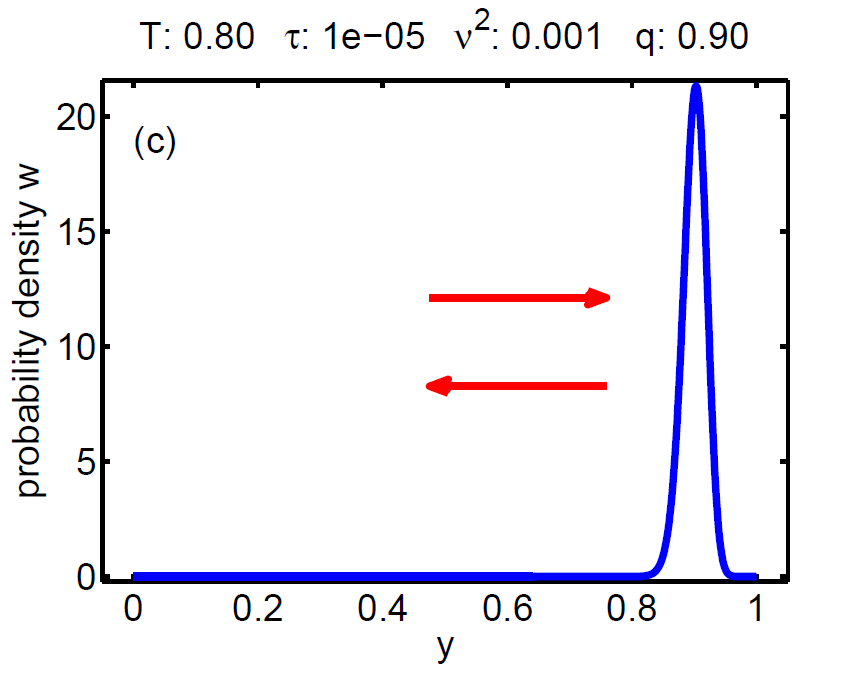
| Figure 7: Evolution of the probability density W(t, y) according a loading-unloading process. | ||||
The probability density satisfies a partial differential equation of Fokker-Planck type.
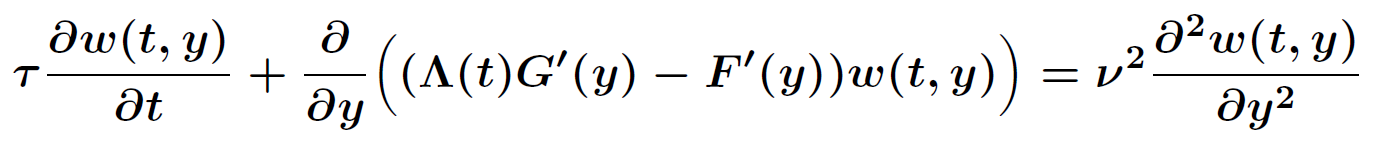 .
.
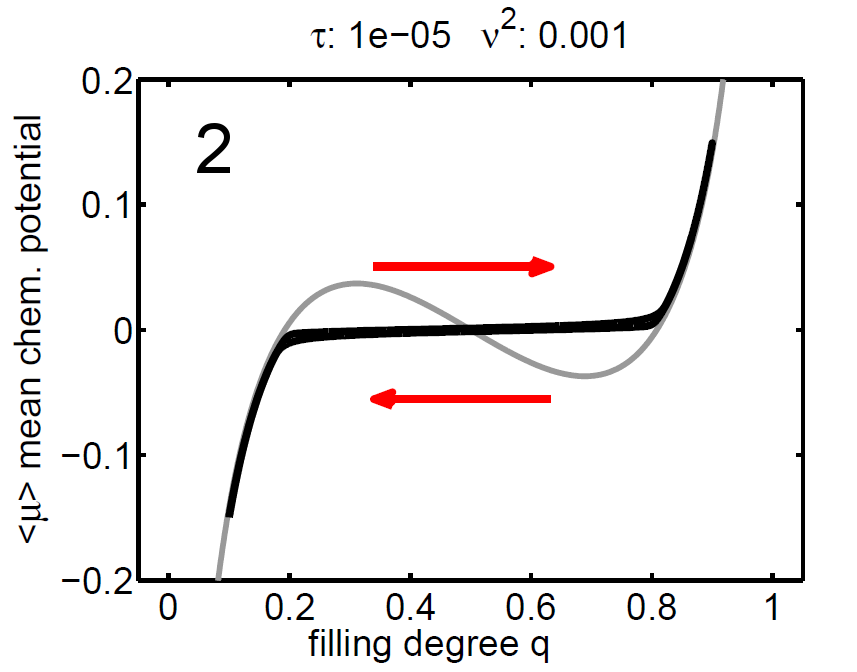
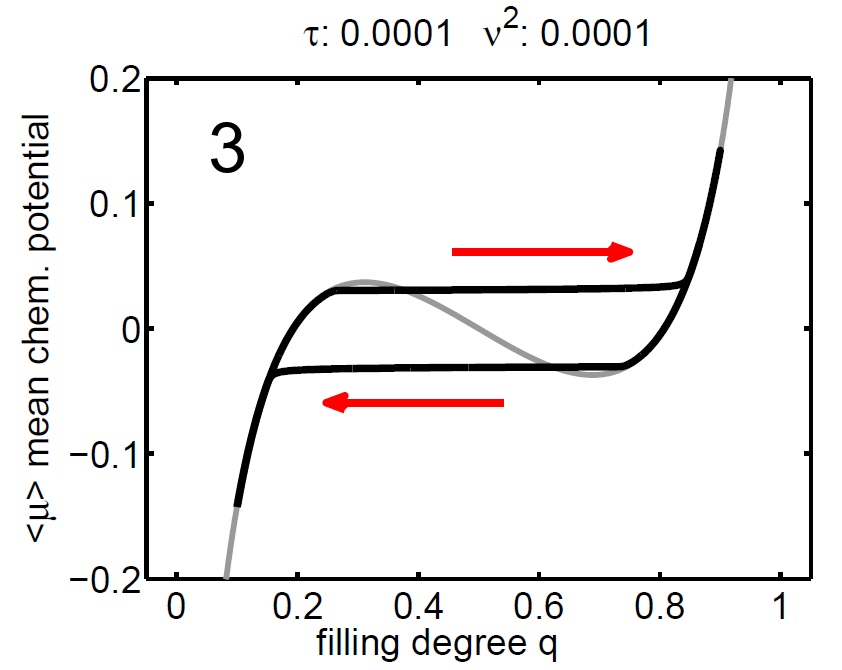
The magnitude of ν2 controls the influence of the mixing entropy of the ensemble and there are three interesting limiting cases:
1. τ > ν2 → no hysteresis, the mean chemical potential follows the non-monotone graph of the single particle potential,
2. τ < ν2 → no hysteresis, the mean chemical potential follows the Maxwell line, and
3. τ ≈ ν2 → hysteretic behaviour.
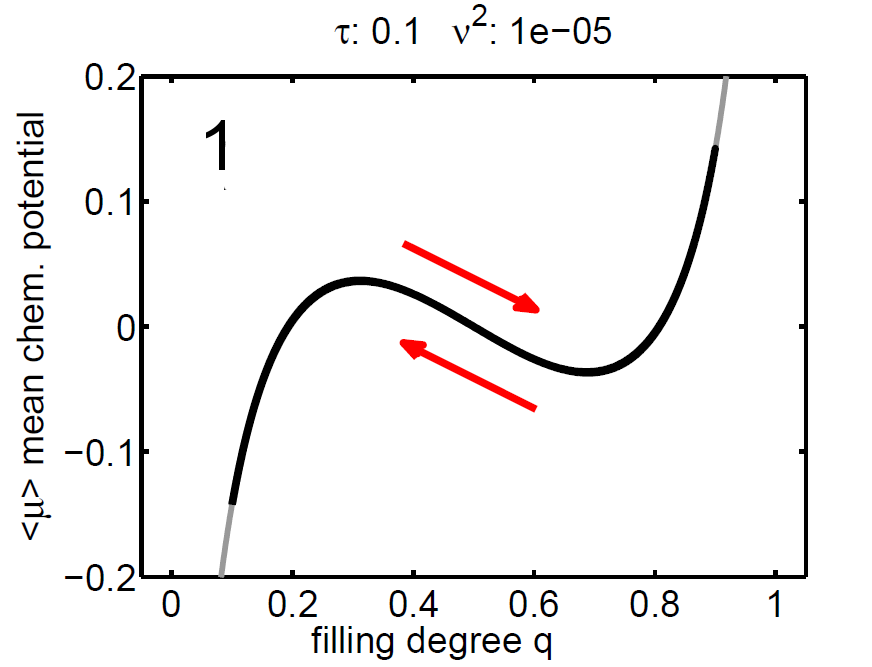
|
|
| ||
| Figure 8: (‹μ›,q) diagram (case 1-3), black: mean chemical potential ‹μ›, gray: chemical potential of single storage particle μ(y). | ||||
|
|
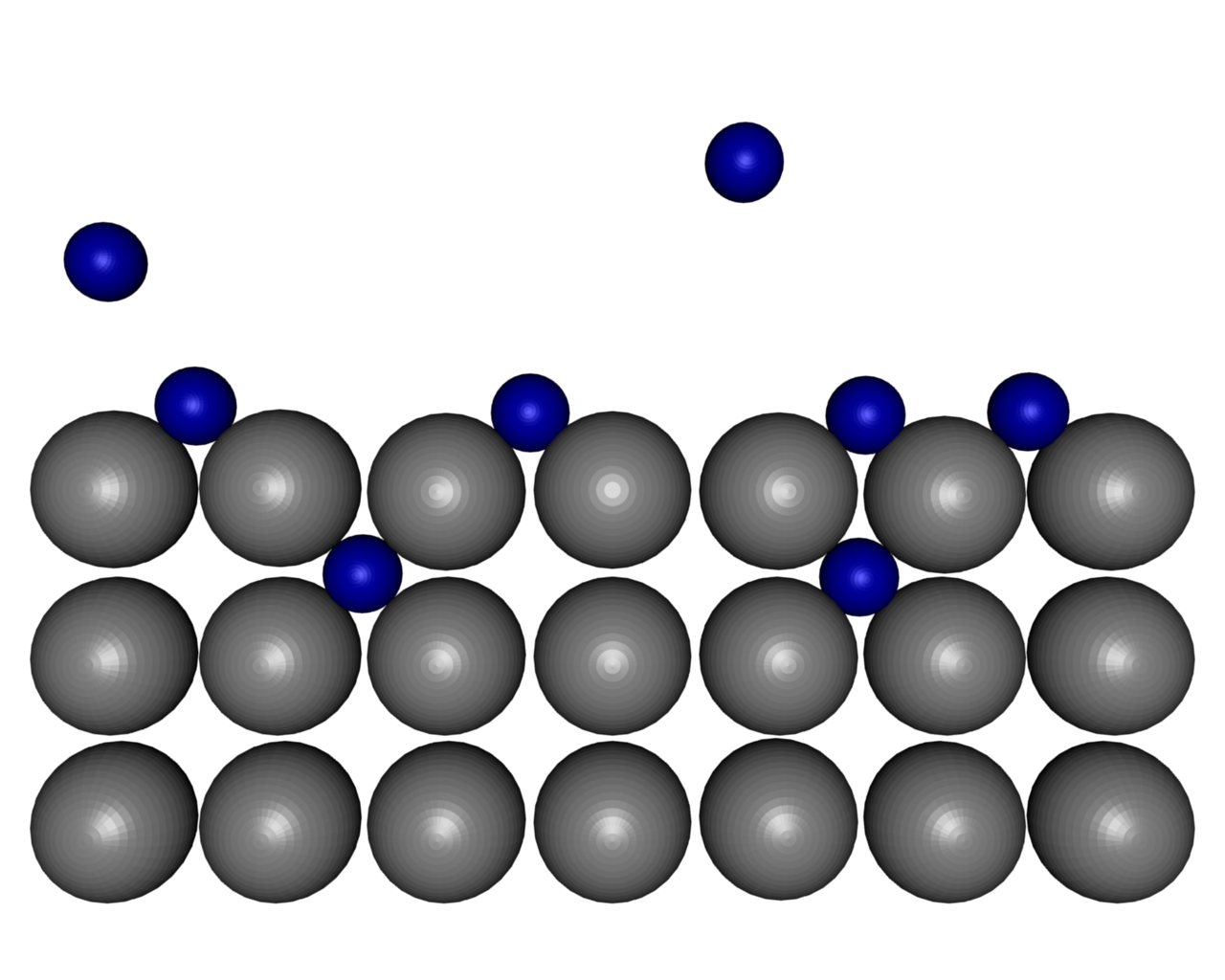
| ||
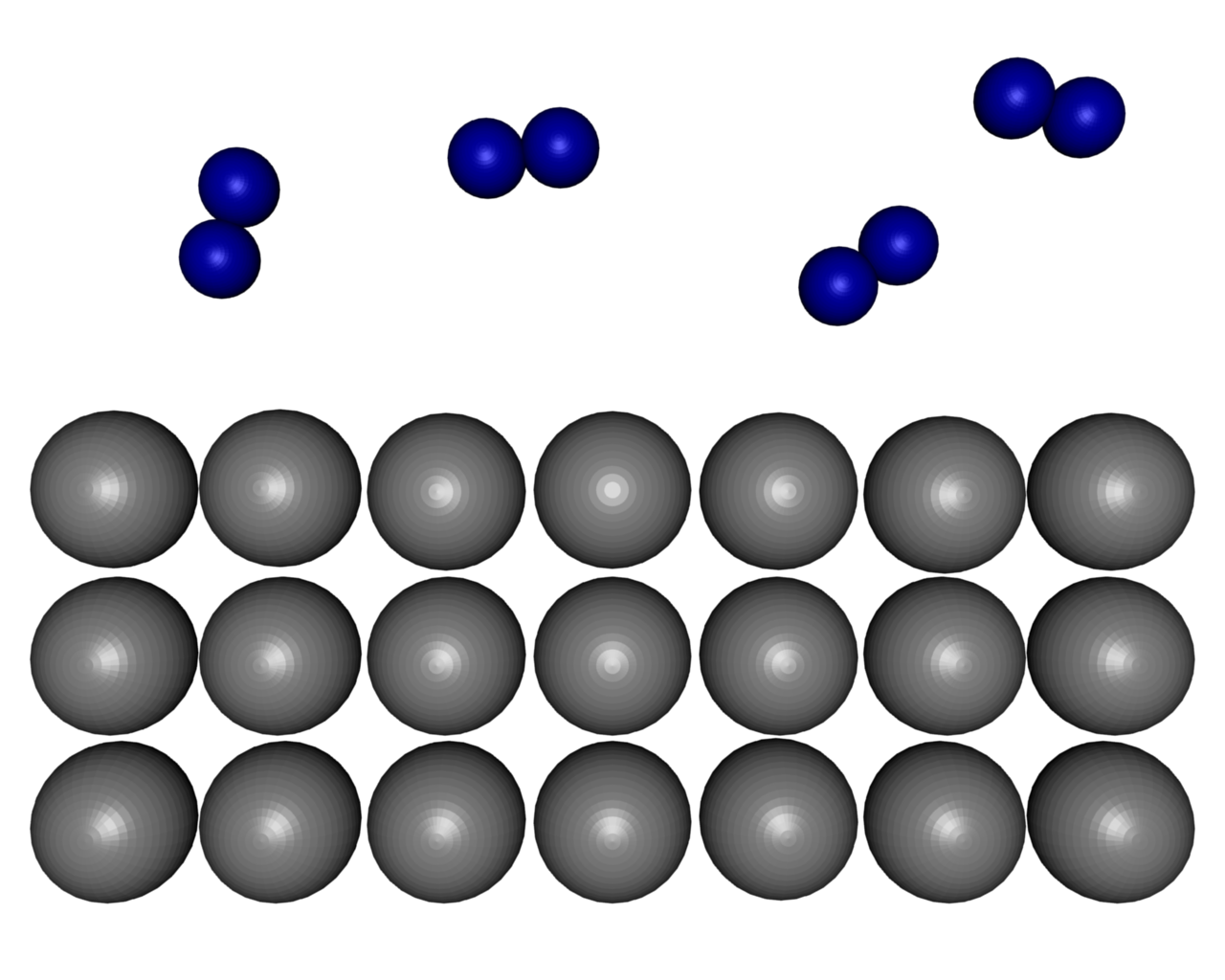
| Figure 9: Dissociation of molecular hydrogen at a Mg-surface. | ||||
Submitted Articles |
|
| [DHMRW11] | W. Dreyer, R. Huth, A. Mielke, J. Rehberg, and M. Winkler Blow-up versus boundedness in a nonlocal and nonlinear fokker-planck equation. WIAS Preprint No. 1604, 2011, submitted to Journal of Nonlinear Science |
Articles in Refereed Scientific Journals |
|
| [DGGHJ11] | W. Dreyer, M. Gaberšček, C. Guhlke, R. Huth and J. Jamnik, Phase transition in a rechargeable lithium battery. European Journal of Applied Mathematics, 22(3):267-290, 2011. |
| [DGHu11] | W. Dreyer, C. Guhlke and R. Huth, The behavior of a many-particle electrode in a lithium-ion battery. Physica D, 240(12):1008-1019, 2011. |
| [DGH11] | W. Dreyer, C. Guhlke and M. Herrmann, Hysteresis and phase transition in many-particle storage systems. Continuum Mechanics and Thermodynamics, 23(3):211-231, 2011 |
| [DJGHMG10] | W. Dreyer, J. Jamnik, C. Guhlke, R. Huth, J. Moškon and M. Gaberšček, The thermodynamic origin of hysteresis in insertion batteries. Nature Materials,(9):448-453, 2010 |
Preprints |
|
| [DGH09a] | W. Dreyer, C. Guhlke and R. Huth, Hysteresis in the context of hydrogen storage and lithium-ion batteries. WIAS Preprint No. 1410, 2009. |
Selected Talks |
|
| 01/31/2012:
Modelling, analysis and simulations of a many-particle cathode of a lithium-ion battery, Fraunhofer ITWM, Kaiserslautern |
|
| 10/05/2011:
Modelling and simulations of the electrolyte-cathode coupling of lithium-ion battery, Battery Days, Konstanz |
|
| 06/17/2010:
Hysteresis and phase transition in many-particle storage systems, HYP 2010, Beijing |
|
| 11/02/2011:
Luftballons, Lithium-Ionen-Batterien und Wasserstoffautos - Ein Fall für die Mathematik!, MathInside, Urania Berlin |
|
| 12/19/2011:
Luftballons, Lithium-Ionen-Batterien und Wasserstoffautos - Ein Fall für die Mathematik!, Rent The Center, Klax-Sekundarschule, Berlin |
|