So, like actors on the classical markets, both producers and large scale consumers of energy face risks and seek protection from these risks by structured contracts, so-called energy derivatives. In the gas and electricity markets for example, so called ``swing options'' have become very popular. A typical swing option gives the holder the right to buy or sell a certain amount of gas, electricity or storage capacity at a certain prescribed number of trading dates. Another issue in the energy markets is the fact that some forms of energy (in particular, oil, gas, and hydro-electric power) can be stored physically. Storage facilities thus allow for anticipating and exploiting market fluctuations of energy prices. Initially, such facilities were only accessible by major players in the respective industries but meanwhile, due to the emerging liberalization of the energy markets, all participants have the possibility to trade storage services via storage exchange platforms. As a consequence, market players are faced with optimal decision problems involving, for example, buying, storing, or selling energy over time, exercising certain energy contracts and so on. Therefore, on the one hand, design of optimal strategies for complexly structured decision problems is called for, and on the other hand, a high demand of adequate statistical prediction algorithms based on adequate statistical modeling of market prices is arisen.
The distinctive properties of energy markets make the existent repertoire of statistical methods and stochastic algorithms developed in the framework of classical financial mathematics insufficient and call for the development of new tailored methods. For example, finding correct prices for energy derivatives is typically difficult due to their complex structured exercise features and their highly path-dependent structure. When developing strategies for energy producers and/or traders, both the particularities of the energy market and the constraints posed by the limited storage and production resources of the actor have to be adequately modeled. As a general consequence, the rising complexity of the markets poses challenging mathematical problems that may be categorized into the following main streams:

• Advanced methods for solving complex decision problems
• Adequate modeling of underlying dynamics, such as energy price processes

Generally, the aim of solving an optimal decision problem, that is an optimal stopping or optimal control problem, is twofold. On the one hand, one aims at bounding its ``true'' value from below and above, and on the other hand one tries to find a ``good'' decision policy consistent with these bounds. In fact, a ``good'' (primal) decision policy yields a lower bound, and a ``good'' system of (dual) martingales yields an upper bound to the ``true'' value, respectively. Thus, naturally, solution methods for optimal decision problems can be classified in primal and dual approaches. For the standard optimal stopping problem, [BBS] succeeded to avoid the time consuming sub-simulations in the Andersen-Broadie algorithm by constructing the dual martingale via a discrete Clark-Ocone derivative of some approximation to the Snell-envelope, obtained by regression on a suitable set of basis functions. Later on in [SZH] a related regression method was developed that also avoids sub-simulations and, even more, does not require any input approximation to the solution of the problem (i.e. the Snell envelope). Particularly the later approach looked promising for generalization to quite general control problems. In this respect, in a preceding project SE-7, Optimizing strategies in energy and storage markets, a framework for regression based methods based on the dual martingale approach has been developed for solving quite general decision problems. 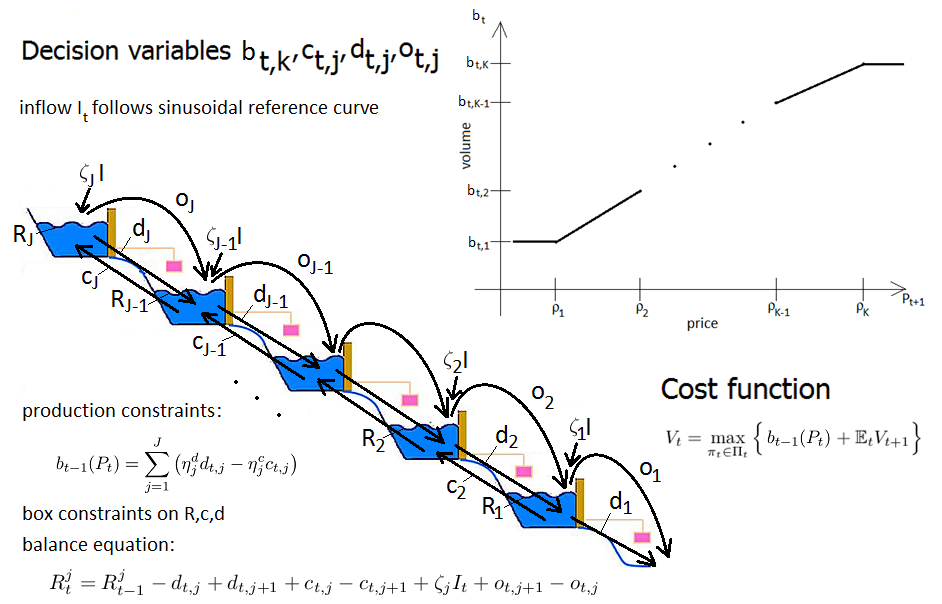As a first non-trivial application, this method was successfully applied in the context of a hydro electricity storage model HSZ16. One of the main goals in this project is a systematic numerical treatment of generic optimal decision problems in ``real-life'' applications by incorporating recent ideas of a relatively new concept of data analysis and prediction: Deep Learning. On the other hand, we include principles of Deep Learning in methods for forecasting and estimating price distribution processes in a systematic way.

Typical ``real-life'' applications have a high dimensional nature and an effective numerical treatment of optimal stopping or control problems in this context, both from the primal and the dual side, is of prime importance and is considered a challenge from a mathematical point of view. In the recent work [HSZ16] a regression based framework was developed that, in principle, allows for simulating an upper biased bound and a lower biased bound to the solution to an optimal decision problem. As a main feature, the approach in [HSZ16] does not require nested simulation. However, there are fundamental problems that need to be tackled. In particular, in the dual approach the stochastic representation of the optimal solution requires in general a set of martingales with a cardinality equal to the typically high number of possible decisions. Further, recursive backward construction of a set of dual martingales in terms of a suitable set of basis functions involves, in principle, an optimization problem that is nonlinear at each step. In general, regression methods in stochastic optimal control heavily rely on the choice of the set of basis functions and in this respect backward construction of the set of dual martingales can be naturally combined with the Deep Learning idea. In particular, the solution from one layer may be incorporated in the set of basis functions for all higher layers. Summing up, the main goals in this project are:

• Combination of regression methods
• Development of new generic methods for solving nonlinear stochastic optimization problems
• Development of a systematic way of estimating underlying price distribution processes

With Prof. Denis Belomestny from Duisburg-Essen University we cooperate on topics in Deep Learning and on theoretical analysis of regression based simulation methods connected with the field of empirical processes.