Project SE2: Electrothermal modeling of large-area OLEDs
This research is carried out in the framework of Matheon supported by Einstein Foundation Berlin
Priv.-Doz. Dr. Annegret Glitzky and Prof. Dr. Alexander Mielke
Staff: Collaboration:Dr. Jürgen Fuhrmann, Dr. Thomas Koprucki, and Dr. Duy Hai Doan
External Cooperation:Dr. Axel Fischer, Priv. Doz. Dr. Reinhard Scholz from Institut für Angewandte Photophysik der TU Dresden
Internal Cooperation:Project background
Organic Light-Emitting Diodes (OLEDs) are thin-film multilayer devices based on organic molecules or polymers. These devices are not only used as displays, but they also occur in intelligent lighting applications. Despite their increasing use in commercial products many technical issues in the development of flat-panel OLED lightings, e.g. spatially non-uniform light emission due to self-heating, still exist. Therefore, accurate methods for modeling the electronic properties combined with the thermal management are needed to design efficient and temperature-tolerant device structures.
Aim of project SE2
The aim of the Matheon project SE2 is to find adequate spatially resolved PDE models that describe the interplay between current and heat flow leading to self-heating and thermal switching phenomena in organic semiconductor devices. Moreover, the project intends to investigate their analytical properties, derive suitable numerical approximation schemes, and provide simulation results which can help to optimize large-area organic light emitting diodes.
Schematic cross section of an OLED stack. (More)
Schematic cross section of OLED stack
OLEDs are millimeter-thin glass wafers with organic materials enclosed in them. In between, an OLED consists of several organic semiconducting layers, which are enclosed by an anode and a cathode layer, that function as the electrical contacts from both sides. The organic layer contains molecules which begin to glow when an electric current passes through them. The particular molecular structure determines the color of the light. The organic layers are coated to protect them from external effects.
Thermistor modeling
For organic semiconductor devices the Arrhenius law applies: The electric conductivity increases with rising temperature. Therefore the electrical current increases and the device gets hotter, resulting in a feedback loop which continuously heats up the entire structure. Experiments show that this effect often leads to the destruction of the device if the heat cannot be dispersed into the environment, see Fischer et al. 2012. It was demonstrated in Fischer et al. 2013 that organic devices with small active areas can be described by a zero-dimensional thermistor model, where the isothermal current-voltage relation for the circuit is given by a power law and a temperature-dependent conductivity factor resulting from an Arrhenius law. Here, the crucial parameter is the so-called activation energy of the material that describes the disorder in the system. For sufficiently high activation energies the self-heating of the device results in S-shaped current-voltage characteristics with negative differential resistance resulting in hysteretic behavior and electric bistability.
Spatially resolved PDE modeling
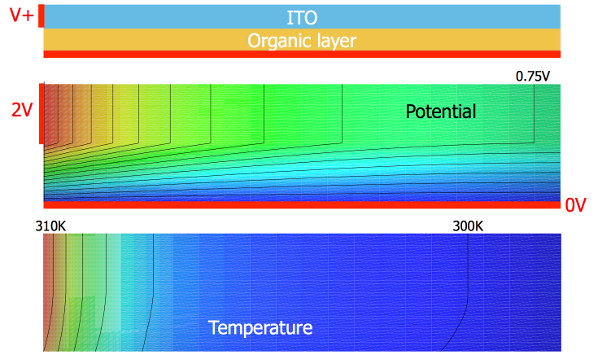
In Fischer et al. 2014, S-shaped IV curves were experimentally verified for OLED structures using 4-wire measurements. Due to the high sheet resistance of the optically transparent electrode and the corresponding lateral voltage drop, spatial dependence is introduced. In this case, the zero-dimensional thermistor has to be replaced by an array of electrically and thermally coupled thermistors to explain the observed formation of inhomogeneities in the luminance.
Based on these equivalent circuit models, in Liero et al. 2015 a stationary PDE thermistor model was derived, which is more flexible in view of numerical simulation and analytical treatment. It consists of the heat equation for the temperature coupled to the current-flow equation for the electrostatic potential with mixed boundary conditions. In particular, it features the same Arrhenius-like temperature law and non-Ohmic behavior of the organic layers. More details
Analysis for p(x)-Laplace thermistor models
The existence of solutions for the p-Laplace thermistor problem for constant exponent p ≥ 2 in two dimensions was first shown in Liero et al. 2015. Known techniques for the treatment of the p(x)-Laplace terms fail in the setting of organic devices since they suppose a log-Hölder continuous dependency of p(x). Generalizations to variable discontinuous exponents p and higher spatial dimensions can be found in Glitzky-Liero 2015 and Bulíček-Glitzky-Liero 2015.
As a first approach, in Glitzky-Liero 2015 a discontinuous, piecewise constant exponent p(x) ≥ 2 was considered in two dimensions. A novel higher integrability results for the gradient of the electrostatic potential was proved by means of localization, Caccioppoli estimates, and Gehring-type arguments. The resulting higher integrability of the Joule heat term in the heat flow equation allows to prove the solvability of the p(x)-Laplace thermistor problem by Schauder’s fixed-point theorem.
A second approach is presented in Bulíček-Glitzky-Liero 2015. Therein, higher spatial dimensions and arbitrary exponents p(x) are considered. The existence proof is based on a regularized version of the thermistor system, where the crucial Joule heat term is approximated such that it remains bounded. The existence of solutions to the regularized problem is proven by Galerkin approximations. By using suitable test functions for the regularized system, uniform estimates independent of the regularization parameter were derived, which allows to pass to the limit and to obtain at least one weak solution to the p(x)-Laplace thermistor problem.
S-shaped current-voltage characteristics in organic devices. (More)
S-curves in organic devices
Self-consistent S-shaped current-voltage characteristics for different activation energies (red). For activation above 4kBT0 they show regions of negative differential resistance (red dashed). Blue: Isothermal current-voltage curve.
Numerical schemes
A finite-volume approximation of the full PDE thermistor model was introduced in Liero et al. 2015, where an accurate implementation of the non-standard electrical conductivity law and the Joule heat expression in the case of non-Ohmic materials is included. Test cases for p(x)-Laplace-type problems with piecewise constant, but considerably jumping p show the stability and performance of the scheme. The most challenging task is the computation of the S-shaped IV curves. Following the ideas by J. Fuhrmann and K. Gärtner path-following techniques where included to overcome the intrinsic instabilities in the system and to compute complete S-shaped characteristics.
Software
We are developing a software tool for the simulation of the interplay between current and heat flow in large-area OLEDs. In particular, we solve the thermistor problem detailed in Liero et al. 2015 in 1D, 2D, and 3D using finite-volume methods. This is based on the PDELib2 toolbox developed at the Weierstrass Institute.
Solutions of p(x)-Laplace thermistor system in 2D. (More)
Solutions of thermistor system
Electrostatic potential (middle) and temperature distribution (bottom) for a simple 2D OLED structure for an applied voltage of 2V (scaled plot).
Events
We organized the workshop "AMaSiS 2015: Applied Mathematics and Simulation for Semiconductors". The workshop took place from March 11-13, 2015 at WIAS Berlin.
In cooperation with ECMath project SE4, A. Glitzky and T. Koprucki coorganized of the Kick-off meeting for the ECMI Special Interest Group "Sustainable Energy" (December 8-9, 2014 at TU Berlin). In the associated workshop "Nanostructures for Photovoltaics and Energy Storage" a session on "Electrical and electrothermal modeling and simulation of organic materials and devices" was initiated.
