xxxxxxxxxx
 
begin 
    ENV["LANG"]="C"
    using Pkg
    Pkg.activate(mktempdir())
    using Revise
    Pkg.add("Revise")
    Pkg.add(["PyPlot","PlutoUI","ExtendableGrids","GridVisualize", "VoronoiFVM"])
    using PlutoUI,PyPlot,ExtendableGrids,VoronoiFVM,GridVisualize
    PyPlot.svg(true)
end;

35.7 s

Finite volumes: transient problems

4.5 μs

Construction of control volumes

Start with a triangulation of a polygonal domain (intervals in 1D,triangles in 2D, tetrahedra in 3D).
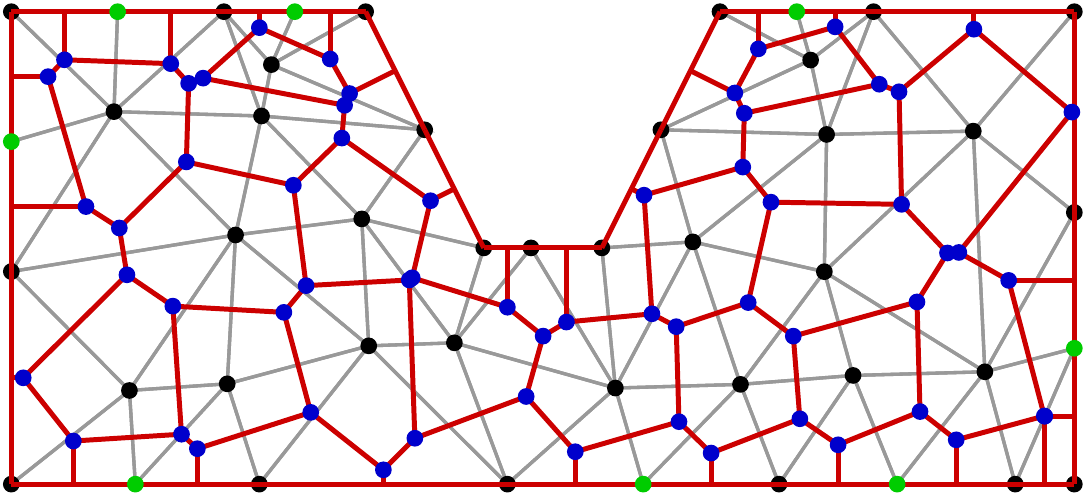
Join triangle circumcenters by lines $\to$ create Voronoi cells which can serve as control volumes, akin to representative elementary volumes (REV) used to derive conservation laws.

Black + green: triangle nodes
Gray: triangle edges
Blue: triangle circumcenters
Red: Boundaries of Voronoi cells

30.1 ms

Condition on triangulation

There is a 1:1 incidence between triangulation nodes and Voronoi cells. Moreover, the angle between the interface between two Voronoi cells and the edge between their corresponding nodes is $\frac{π}{2}$ .
Requires (in 2D) that sums of angles opposite to triangle edges are less than $π$ and that angles opposite to boudary edges are less than $\frac{π}{2}$ .
"boundary conforming Delaunay property". It has different equivalent definitions and analogues in 3D.
Construction:
- "by hand" (or script) from tensor product meshes
- Mesh generators: Triangle, TetGen
- Julia packages: Triangulate.jl, TetGen.jl; SimplexGridFactory.jl

2.2 ms

The discretization approach

Use Voronoi cells as REVs aka control volumes aka finite volume cells.

17.1 μs

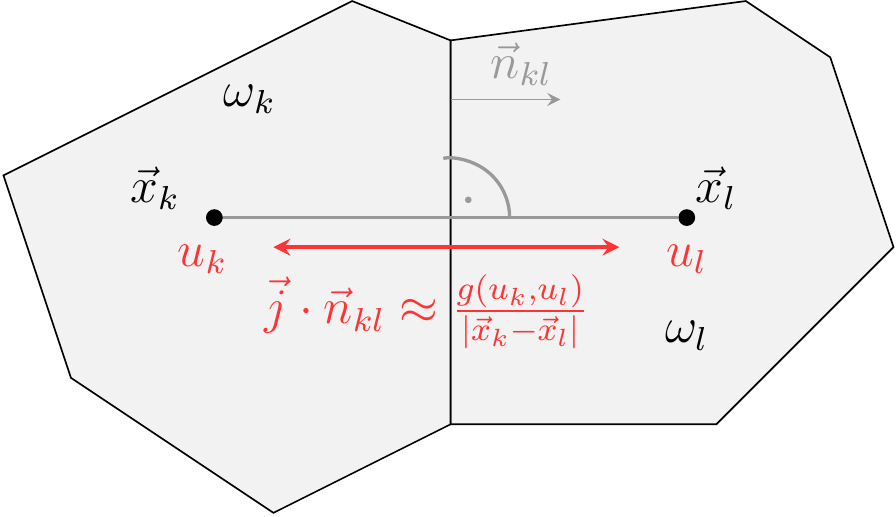
Given a continuity equation $\nabla \cdot \vec{j} = 0$ in a domain $Ω$ , integrate this over a contol volume $ω_{k}$ with associated node ${\vec{x}}_{k}$ and apply Gauss theorem:

$\begin{aligned} 0 & = \int_{ω_{k}} \nabla \cdot \vec{j} d ω = \int_{\partial ω_{k}} \vec{j} \cdot \vec{n} d s \\ = \sum_{l \in N_{k}} \int_{ω_{k} \cap ω_{l}} \vec{j} \cdot \vec{n} d s + \int_{\partial ω_{k} \cap \partial Ω} \vec{j} \cdot \vec{n} d s \\ \approx \sum_{l \in N_{k}} \frac{σ_{k l}}{h_{k l}} g (u_{k}, u_{l}) + γ_{k} b (u_{k}) \end{aligned}$

Here, $N_{k}$ is the set of neighbor control volumes, $σ_{k l} = | ω_{k} \cap ω_{l} |$ , $h_{k l} = | {\vec{x}}_{k} - {\vec{x}}_{l} |$ , $γ_{k} = | \partial ω_{k} \cap \partial Ω |$ , where $| \cdot |$ denotes the measure (length resp. area) of a geometrical entity.

9.1 μs

Flux functions

For instance, for the diffusion flux $\vec{j} = - D \vec{\nabla} u$ , we use $g (u_{k}, u_{l}) = D (u_{k} - u_{l})$ .

For a convective diffusion flux $\vec{j} = - D \vec{\nabla} u + u \vec{v}$ , one can chose the upwind flux

$\begin{aligned} g (u_{k}, u_{l}) = D (u_{k} - u_{l}) + v_{k l} {\begin{cases} u_{k}, & v_{k l} > 0 \\ u_{l}, & v_{k l} \leq 0, \end{cases} \end{aligned}$

where $v_{k l} = \frac{h_{k l}}{σ_{k l}} \int_{ω_{k} \cap ω_{l}} \vec{v} \cdot {\vec{n}}_{k l} d s$ Fluxes also can depend nonlinearily on $u$ .

6.1 μs

Software API and implementation

$\partial_{t} s (u) + \nabla \cdot \vec{j} (u) + r (u) = f$

The entities describing the discrete system can be subdivided into two categories:

geometrical data: $| ω_{k} |, γ_{k}, σ_{k l}, h_{k l}$ together with the connectivity information of the triangles
physical data: the number $m$ and the functions $s, g, r, f$ describing the particular problem, where $g$ is a flux function approximating $\vec{j}$ .

This structure allows to describe the problem to be solved by data derived from the discretization grid and by the functions describing the physics, giving rise to a software API.

The solution of the nonlinear systems of equations can be performed by Newton's method combined with various direct and iterative linear solvers.

The generic programming capabilities of Julia allow for an implementation of the method which results in an API which consists in the implementation of functions $s, g, r, f$ without the need to write code for their derivatives.

8.1 μs

Examples

General settings

Initial value problem with homgeneous Neumann boundary conditions

$Ω = (0, 1)^{d}, d = 1, 2$

$T = [0, t_{e n d}]$

5.6 μs

evolution (generic function with 1 method)

xxxxxxxxxx
 
# Function describing evolution of system with initial value inival 
# using the Implicit Euler method
function evolution(inival, # initial value
                   sys,    # finite volume system
                   grid,   # simplex grid
                   tstep,  # initial time step 
                   tend,   # end time 
                   dtgrowth  # time step growth factor
                   )
    time=0.0
    # record time and solution
    times=[time]
    solutions=[copy(inival)]
    
    solution=copy(inival)
    while time<tend
        time=time+tstep
        solve!(solution,inival,sys,tstep=tstep) # solve implicit Euler time step 
        inival.=solution  # copy solution to inivalue
        push!(times,time) 
        push!(solutions,copy(solution))
        tstep*=dtgrowth  # increase timestep by factor when approaching stationary state
    end
    # return result and grid 
    (times=times,solutions=solutions,grid=grid)
end
​

34.8 μs

fpeak (generic function with 2 methods)

xxxxxxxxxx
 
# Define function for initial value $u_0$ with two methods - for 1D and 2D problems
begin
    fpeak(x)=exp(-100*(x-0.25)^2)
    fpeak(x,y)=exp(-100*((x-0.25)^2+(y-0.25)^2))
end

40.6 μs

create_grid (generic function with 1 method)

xxxxxxxxxx
 
# Create discretization grid in 1D or 2D with approximately n nodes
function create_grid(n,dim)
    nx=n
    if dim==2
        nx=ceil(sqrt(n))
    end
    X=collect(0:1.0/nx:1)
    if dim==1
      grid=simplexgrid(X)
    else
      grid=simplexgrid(X,X)
    end
end

51.8 μs

Diffusion problem

$\partial_{t} u - \nabla \cdot D \nabla u = 0 in Ω$

$D \nabla u \cdot \vec{n} = 0 on \partial Ω$

$u |_{t = 0} = u_{0}$

2.7 μs

diffusion (generic function with 1 method)

xxxxxxxxxx
 
function diffusion(;n=100,dim=1,tstep=1.0e-4,tend=1, D=1.0, dtgrowth=1.1)
    grid=create_grid(n,dim)
    
    ## Diffusion flux between neigboring control volumes
    function flux!(f,u,edge)
        uk=viewK(edge,u)  
        ul=viewL(edge,u)
        f[1]=D*(uk[1]-ul[1])
    end
​
    ## Storage term (under time derivative)
    function storage!(f,u,node)
        f[1]=u[1]
    end
​
    ## Create a physics structure
    physics=VoronoiFVM.Physics(
        flux=flux!,
        storage=storage!)
    
    sys=VoronoiFVM.DenseSystem(grid,physics)
    enable_species!(sys,1,[1])
    
    ## Create a solution array
    inival=unknowns(sys)
​
    ## Broadcast the initial value
    inival[1,:].=map(fpeak,grid)
​
    evolution(inival,sys,grid,tstep,tend,dtgrowth)
end 

91.4 μs

xxxxxxxxxx
 
result_diffusion=diffusion(dim=1,n=1000);

6.8 s

time=

23.6 ms

51.7 ms

Reaction-diffusion problem

Diffusion + physical process which "eats" species

$\partial_{t} u - \nabla \cdot D \nabla u + R u = 0 in Ω$

$D \nabla u \cdot \vec{n} = 0 on \partial Ω$

$u |_{t = 0} = u_{0}$

3.3 μs

reaction_diffusion (generic function with 1 method)

xxxxxxxxxx
 
​
function reaction_diffusion(;
        n=1000,
        dim=1,
        tstep=1.0e-4,
        tend=1, 
        D=1.0, 
        R=10.0, 
        dtgrowth=1.1)
​
    grid=create_grid(n,dim)
    ## Diffusion flux between neigboring control volumes
    function flux!(f,u,edge)
        uk=viewK(edge,u)  
        ul=viewL(edge,u)
        f[1]=D*(uk[1]-ul[1])
    end
​
    ## Storage term (under time derivative)
    function storage!(f,u,node)
        f[1]=u[1]
    end
​
    ## Reaction term
    function reaction!(f,u,node)
        f[1]=R*u[1]
    end
​
  
    ## Create a physics structure
    physics=VoronoiFVM.Physics(
        flux=flux!,
        reaction=reaction!,
        storage=storage!)
    
    sys=VoronoiFVM.DenseSystem(grid,physics)
    enable_species!(sys,1,[1])
    ## Create a solution array
    inival=unknowns(sys)
    
    ## Broadcast the initial value
    inival[1,:].=map(fpeak,grid)
​
    evolution(inival,sys,grid,tstep,tend,dtgrowth)  
end

112 μs

xxxxxxxxxx
 
result_reaction_diffusion=reaction_diffusion(dim=1,n=1000,R=10);

1.7 s

time=

96.3 μs

57.3 ms

Convection-Diffusion problem

$\partial_{t} u - \nabla \cdot (D \nabla u - u \vec{v}) = 0 in Ω$

$(D \nabla u - u \vec{v}) \cdot \vec{n} = 0 on \partial Ω$

$u |_{t = 0} = u_{0}$

3.0 μs

convection_diffusion (generic function with 1 method)

xxxxxxxxxx
 
function convection_diffusion(;
        n=20,
        dim=1,
        tstep=1.0e-4, 
        tend=1, 
        D=0.01, 
        vx=10.0,
        vy=10.0,
        dtgrowth=1.1, 
        scheme="expfit")
   grid=create_grid(n,dim)
   # copy vx, vy into vector
   if dim==1
        V=[vx]
   else
        V=[vx,vy]
   end
   # Bernoulli function
    
    
    B(x)=x/(exp(x)-1)
 
    function flux_expfit!(f,u,edge)
        uk=viewK(edge,u)  
        ul=viewL(edge,u)
        vh=project(edge,V)  # Calculate projection v * (x_L-x_K)
        f[1]=D*(B(-vh/D)*uk[1]- B(vh/D)*ul[1])
    end
    
    function flux_centered!(f,u,edge)
        uk=viewK(edge,u)  
        ul=viewL(edge,u)
        vh=project(edge,V)
        f[1]=D*(uk[1]-ul[1])+ vh*0.5*(uk[1]+ul[1])
    end
    
    function flux_upwind!(f,u,edge)
        uk=viewK(edge,u)  
        ul=viewL(edge,u)
        vh=project(edge,V)
        f[1]=D*(uk[1]-ul[1])+ ( vh>0.0 ? vh*uk[1] : vh*ul[1] )
    end
    
    flux! =flux_upwind!
    if scheme=="expfit"
        flux! =flux_expfit!
    elseif scheme=="centered"
        flux! =flux_centered!
    end
    
    
    ## Storage term (under time derivative)
    function storage!(f,u,node)
        f[1]=u[1]
    end
​
    ## Create a physics structure
    physics=VoronoiFVM.Physics(
        flux=flux!,
        storage=storage!)
    
    sys=VoronoiFVM.DenseSystem(grid,physics)
    enable_species!(sys,1,[1])
    ## Assume homogeneous Neumann boundary conditions, so do nothig
    
    ## Create a solution array
    inival=unknowns(sys)
    
    ## Broadcast the initial value
    inival[1,:].=map(fpeak,grid)
    evolution(inival,sys,grid,tstep,tend,dtgrowth)  
end 
​

144 μs

scheme:

115 ms

xxxxxxxxxx
 
result_convection_diffusion=convection_diffusion(n=100,
    dim=1,
    scheme=scheme[1],
    vx=10,vy=10);

38.1 ms

time=

48.7 μs

72.6 ms

Brusselator system

Two species interacting via a reaction:

$\begin{aligned} \partial_{t} u_{1} - \nabla \cdot (D_{1} \nabla u_{1}) & + (B + 1) u_{1} - A - u_{1}^{2} u_{2} = 0 \\ \partial_{t} u_{2} - \nabla \cdot (D_{2} \nabla u_{2}) & + u_{1}^{2} u_{2} - B u_{1} = 0 \end{aligned}$

3.2 μs

brusselator (generic function with 1 method)

xxxxxxxxxx
 
function brusselator(;n=100,dim=1,A=4.0,B=6.0,D1=0.01,D2=0.1,perturbation=0.1,
    tstep=0.05, tend=150,dtgrowth=1.05)
​
    grid=create_grid(n,dim)
    function storage!(f,u,node)
        f.=u
    end
​
    
function bruss_diffusion!(f,_u,edge)
        u=unknowns(edge,_u)
    f[1]=D1*(u[1,1]-u[1,2])
    f[2]=D2*(u[2,1]-u[2,2])
end
# Reaction:
function bruss_reaction!(f,u,node)
    f[1]= (B+1.0)*u[1]-A-u[1]^2*u[2]
    f[2]= u[1]^2*u[2]-B*u[1]
end
# Create system
bruss_physics=VoronoiFVM.Physics(flux=bruss_diffusion!,storage=storage!,
                                 num_species=2,reaction=bruss_reaction!)
brusselator_system=VoronoiFVM.DenseSystem(grid,bruss_physics)
enable_species!(brusselator_system,1,[1])
enable_species!(brusselator_system,2,[1])
​
    inival=unknowns(brusselator_system)
for i=1:num_nodes(grid)
    inival[1,i]=1.0+perturbation*randn()
    inival[2,i]=1.0+perturbation*randn()
end
​
    evolution(inival,brusselator_system,grid,tstep,tend,dtgrowth)   
end
​

119 μs

xxxxxxxxxx
 
result_brusselator=brusselator(n=500,dim=1);

2.3 s

time=

46.2 μs

122 ms

3.9 ms

Status `/tmp/jl_op3lMf/Project.toml`
  [cfc395e8] ExtendableGrids v0.7.4
  [5eed8a63] GridVisualize v0.1.3
  [7f904dfe] PlutoUI v0.7.2
  [d330b81b] PyPlot v2.9.0
  [295af30f] Revise v3.1.12
  [82b139dc] VoronoiFVM v0.10.5

1.5 s