Collaborator: D. Rachinskii
Cooperation with: M. Brokate (Technische Universität München),
A.M. Krasnosel'skii, V.S. Kozyakin (Institute for Information
Transmission Problems, Moscow, Russia), A.V. Pokrovskii, O. Rasskazov
(University College Cork, Ireland)
Description:
Localization of periodic orbits
is one of the basic problems in the
analysis and control of dynamical systems. Using methods of
topological degree theory, we have developed new analytic approaches
to nonlocal problems on periodic solutions of systems with
nonlinearities of saturation type, which are typical particularly
for problems of laser dynamics.
We have studied bifurcations of periodic solutions from infinity and
obtained estimates for the number of, and asymptotic formulas for,
solution branches, [1, 2]. It was proved that
generically there are two branches of forced periodic oscillations.
However, many (any even number of) branches may appear in degenerate
situations, which are standard for problems on subharmonic
solutions. We have derived sufficient conditions for the existence
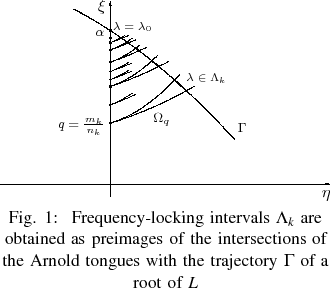
of subharmonics (periodic solutions of multiple periods 2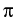 n)
with arbitrarily large amplitudes and periods for higher-order
ordinary differential equations
n)
with arbitrarily large amplitudes and periods for higher-order
ordinary differential equations
 depending on a scalar
parameter
depending on a scalar
parameter 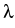 , with a 2
, with a 2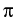 -periodic forcing term b and a
nonlinearity f with saturation. This type of a subharmonic
bifurcation from infinity occurs ([3]) whenever a pair of
simple roots
-periodic forcing term b and a
nonlinearity f with saturation. This type of a subharmonic
bifurcation from infinity occurs ([3]) whenever a pair of
simple roots
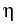 (
(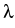 )
)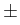
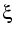 (
(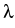 )i of the characteristic
polynomial L crosses the imaginary axis at points
)i of the characteristic
polynomial L crosses the imaginary axis at points
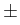
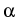 i
with an irrational
i
with an irrational 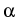 . Under some further assumptions, we have
estimated the parameter intervals of frequency locking, where
subharmonics with amplitudes and periods increasing to infinity
appear sporadically as the parameter approaches a bifurcation value
. Under some further assumptions, we have
estimated the parameter intervals of frequency locking, where
subharmonics with amplitudes and periods increasing to infinity
appear sporadically as the parameter approaches a bifurcation value
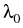 . These assumptions relate the quality of the rational
Diophantine approximations of
. These assumptions relate the quality of the rational
Diophantine approximations of 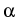 , the rate of convergence of
the nonlinearity to its limits at infinity, and the smoothness of
the forcing term. Actually, our results provide estimates for the
width and length of the Arnold tongues in the problem of bifurcation
of subharmonics from infinity (see Figure 1).
, the rate of convergence of
the nonlinearity to its limits at infinity, and the smoothness of
the forcing term. Actually, our results provide estimates for the
width and length of the Arnold tongues in the problem of bifurcation
of subharmonics from infinity (see Figure 1).
In [4], we applied our method to a Hopf bifurcation problem
with a multiple resonance. Some numerical aspects of the problems
were considered in [5].
A separate research direction was aimed at understanding the
dynamics of systems where hysteresis
plays an important role. Using
the theory of closed systems with hysteresis operators as a
framework for our studies, and concentrating mostly on periodic and
cyclic processes, their stability and bifurcations, we have observed
that hysteresis may be a source of several specific effects. For
example, systems with hysteresis may have attractors consisting of a
continuum of periodic or quasiperiodic orbits in generic situations.
The results were tested with hysteresis models of different types.
We have studied the structure and stability of nontrivial connected
clusters of periodic orbits that appear from an asymptotically
stable periodic trajectory as a result of a hysteresis perturbation
of the system, [6], as well as Hopf bifurcations of such
attracting clusters from equilibria and from infinity, [7,
8]. A variety of dynamic and bifurcation scenarios (see,
for example, Figure 2) was analyzed for the Duffing-type
forced oscillator
x'' + x = sin(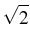 t) + t) + 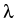 P(x)(t) P(x)(t)
|
(2) |
with the hysteresis friction modeled by the Preisach operator P,
on the basis of new topological approaches developed in
[9], which combine analytic and rigorous computer-aided
methods. Global stability of some complex hysteresis models,
including that with the so-called ratchetting effect (unclosed
hysteresis loops), was studied in [10, 11].
Fig. 2:
Bifurcations of stable periodic orbits of the Poincaré map for
Eq. (2) for different values of the parameter
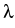 : Two equilibria and two period-2 points (upper left);
bifurcations of the equilibria to clusters of invariant curves
(quasiperiodic orbits) and period doubling bifurcation of the
period-2 orbits to period-4 orbits (upper right); further bifurcations of
the periodic orbits to higher-order subharmonics (lower left);
bifurcation to chaos (lower right)
: Two equilibria and two period-2 points (upper left);
bifurcations of the equilibria to clusters of invariant curves
(quasiperiodic orbits) and period doubling bifurcation of the
period-2 orbits to period-4 orbits (upper right); further bifurcations of
the periodic orbits to higher-order subharmonics (lower left);
bifurcation to chaos (lower right)
![\makeatletter
\@VierProjektbilderNocap[q]{0.25\textwidth}{fig2_rach_2.eps}{fig2_rach_3.eps}{fig2_rach_4.eps}{fig2_rach_5.eps}
\makeatother](img230.gif) |
References:
- A.M. KRASNOSEL'SKII, D.I. RACHINSKII, Branching at
infinity of solutions to equations with degeneration of multiplicity
two, Doklady Math., 69(1) (2004), pp. 79-83.
, On a number of
unbounded solution branches near the asymptotic bifurcation point,
to appear in: Funct. Anal. Appl.
- V.S. KOZYAKIN, A.M. KRASNOSEL'SKII, D.I. RACHINSKII, Subharmonic bifurcation from infinity, submitted.
- A.M. KRASNOSEL'SKII, D.I. RACHINSKII, Remark on the Hopf
bifurcation theorem, Math. Nachr., 272 (2004),
pp. 95-103.
- A.M. KRASNOSEL'SKII, A.V. POKROVSKII, D.I. RACHINSKII, On
guaranteed estimates of convergence rate for one class of iteration
procedures, Autom. Remote Control, 65(10) (2004),
pp. 1635-1640.
- M. BROKATE, A.V. POKROVSKII, D.I. RACHINSKII, Asymptotic
stability of continual sets of periodic solutions to systems with
hysteresis, WIAS Preprint no. 902, 2004.
- M. BROKATE, D.I. RACHINSKII, Hopf bifurcations and simple
structures of periodic solution sets in systems with the Preisach
nonlinearity, WIAS Preprint no. 921, 2004.
- D.I. RACHINSKII, On a bifurcation of stable
large-amplitude cycles for equations with hysteresis, Autom.
Remote Control, 65(12) (2004), pp. 1915-1937.
- M. BROKATE, A.V. POKROVSKII, D.I. RACHINSKII, O. RASSKAZOV,
Differential equations with hysteresis in examples, to appear
in: The
Science of Hysteresis, I. Mayergoyz, G. Bertotti, eds., Elsevier Science, 150 pages.
- M. BROKATE, D.I. RACHINSKII, On global stability of the
scalar Chaboche models, Nonlinear Anal. Real World
Appl., 6 (2005), pp. 67-82.
, Global stability of
Armstrong-Frederick models with periodic uniaxial inputs,
to appear in: NoDEA Nonlinear Differential Equations Appl.
LaTeX typesetting by H. Pletat
2005-07-29
![]() n)
with arbitrarily large amplitudes and periods for higher-order
ordinary differential equations
n)
with arbitrarily large amplitudes and periods for higher-order
ordinary differential equations
 depending on a scalar
parameter
depending on a scalar
parameter ![\makeatletter
\@VierProjektbilderNocap[q]{0.25\textwidth}{fig2_rach_2.eps}{fig2_rach_3.eps}{fig2_rach_4.eps}{fig2_rach_5.eps}
\makeatother](img230.gif)