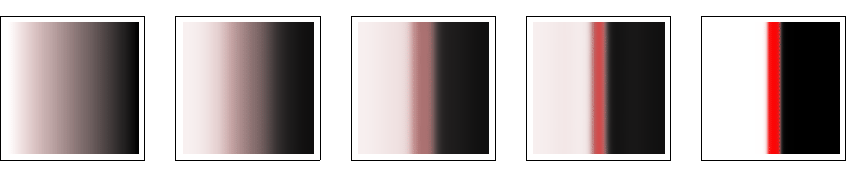Collaborator: J.A. Griepentrog,
H. Gajewski
Description:
To describe phase separation processes
we consider a closed multicomponent system with interacting particles of type
k  {0, 1,..., n} occupying a spatial domain. In our model we assume
that the particles jump around on a given microscopically scaled lattice
following a stochastic exchange process (see [2]).
On each lattice site sits exactly one particle (exclusion principle).
Two particles of type k and l change their sites x and y
with probability
pkl(x, y) due to diffusion and
nonlocal interaction.
The hydrodynamical limit leads to a system of conservation laws
for
k
{0, 1,..., n} occupying a spatial domain. In our model we assume
that the particles jump around on a given microscopically scaled lattice
following a stochastic exchange process (see [2]).
On each lattice site sits exactly one particle (exclusion principle).
Two particles of type k and l change their sites x and y
with probability
pkl(x, y) due to diffusion and
nonlocal interaction.
The hydrodynamical limit leads to a system of conservation laws
for
k  {0, 1,..., n},
{0, 1,..., n},
uk' + 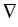 . jk = 0 in
(0, T) x . jk = 0 in
(0, T) x 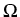 , ,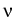 . jk = 0 on
(0, T) x . jk = 0 on
(0, T) x 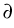 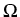 , uk(0) = gk in , uk(0) = gk in 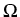 , ,
|
(1) |
for (scaled) particle densities
u0, u1,..., un ,
their initial values
g0, g1,..., gn,
and current densities
j0, j1,..., jn .
Here, (0, T) denotes a time interval and 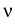 is the outer unit normal
on the boundary
is the outer unit normal
on the boundary
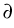
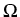 of the bounded m-dimensional
Lipschitz domain
of the bounded m-dimensional
Lipschitz domain 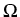 .
Due to the exclusion principle of the stochastic process we can assume
.
Due to the exclusion principle of the stochastic process we can assume
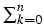 uk = 1,
uk = 1,
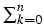 gk = 1, and
gk = 1, and
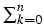 jk = 0, that
means, only n of the n + 1 equations in (1)
are independent of each other. Hence, we can drop out one equation,
say the equation for the zero component, and describe the state of
the system by n-component vectors
u = (u1,..., un)
having in mind the notation
u0 = 1 -
jk = 0, that
means, only n of the n + 1 equations in (1)
are independent of each other. Hence, we can drop out one equation,
say the equation for the zero component, and describe the state of
the system by n-component vectors
u = (u1,..., un)
having in mind the notation
u0 = 1 - 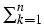 uk .
uk .
To establish thermodynamical relations between current densities,
particle densities, and their conjugated variables,
we minimize the free energy functional
under the constraint of particle number conservation.
In contrast to the classical Cahn-Hilliard theory we consider
diffuse interface models and free energy functionals with nonlocal expressions.
As a straightforward generalization of the nonlocal phase separation model for
binary systems (see [1]) we define
a free energy functional
F = F1 + F2 by
F1(u) = 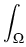 f (u(x)) dx , F2(u) = f (u(x)) dx , F2(u) = 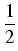 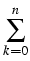 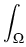 (Ku)k(x) uk(x) dx , (Ku)k(x) uk(x) dx ,
|
(2) |
f (u) = 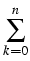 uklog(uk) ,(Ku)k(x) = uklog(uk) ,(Ku)k(x) = 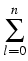 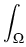 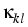 (x, y) ul(y) dy . (x, y) ul(y) dy .
|
(3) |
The convex function f and the symmetric
(n + 1) x (n + 1)-matrix kernel
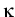 define the chemical part F1 and the
nonlocal interaction part F2 of the functional F, respectively.
Minimizing F under the constraint of particle number conservation,
we identify the conjugated variables of the densities
as grand chemical potential differences
define the chemical part F1 and the
nonlocal interaction part F2 of the functional F, respectively.
Minimizing F under the constraint of particle number conservation,
we identify the conjugated variables of the densities
as grand chemical potential differences
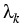
=
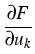
=
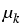
+
wk ,
k 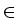
{1,...,
n} ,
where 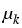 and wk are chemical and
interaction potential differences, respectively,
and wk are chemical and
interaction potential differences, respectively,
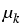 = = 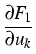 = log(uk) - log(u0) , wk = = log(uk) - log(u0) , wk = 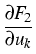 = (Ku)k - (Ku)0 , k = (Ku)k - (Ku)0 , k 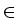 {1,..., n} . {1,..., n} .
|
(4) |
The hydrodynamical limit process (see [2])
yields current densities
jk = -
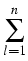 akl
akl(
u)
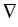
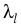
,
k 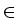
{1,...,
n} ,
where the mobility has the form
a(u) = d (u)(D2f (u))-1,
and d (u) denotes the diffusivity.
Hence, we can interpret the above nonlocal phase separation model as a
system of drift-diffusion equations with semilinear diffusion and
nonlinear nonlocal drift terms, if we rewrite the currents as
jk = -
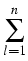 dkl
dkl(
u)
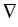 ul
ul -
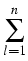 akl
akl(
u)
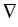 wl
wl ,
k 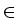
{1,...,
n} .
In [4] we consider the case
dkl = 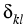 .
Then, an elementary computation of the inverse Hessian matrix
(D2f (u))-1
yields the following expressions for the mobility coefficients
.
Then, an elementary computation of the inverse Hessian matrix
(D2f (u))-1
yields the following expressions for the mobility coefficients
akl(
u) =
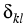 uk
uk -
uluk ,
k,
l 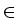
{1,...,
n} .
For the functional analytic formulation of our problem
we use standard spaces
H = [
L2(
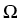
)]
n ,
V = [
H1(
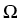
)]
n ,
L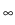
= [
L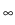
(
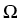
)]
n ,
respectively, and their generalizations suitable for evolution systems,
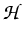
=
L2((0,
T);
H) ,
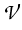
=
L2((0,
T);
V) ,
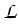
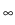
=
L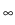
((0,
T);
L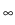
) ,
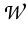
= {
u 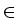
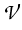
:
u' 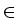
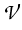 *
*} .
Having in mind
u0 = 1 - 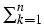 uk ,
we define simplices
S
uk ,
we define simplices
S 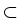 L
L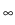 and
and
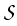
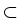
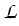
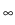 by
by
S = {
g 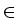 L
L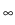
: 0
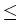 g0
g0,
g1,...,
gn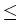
1} ,
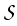
= {
u 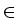
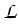
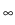
: 0
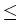 u0
u0,
u1,...,
un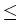
1} .
Furthermore, we introduce the drift-diffusion operator
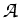 :
: 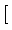
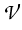
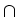
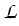
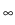
![$ \left.\vphantom{ \mathcal{V} \cap \mathcal{L}^\infty }\right]$](img175.gif) x
x 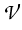
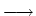
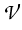 * by
for
(u, w)
* by
for
(u, w) 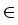
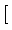
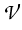
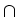
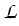
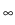
![$ \left.\vphantom{ \mathcal{V} \cap \mathcal{L}^\infty }\right]$](img175.gif) x
x 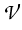 ,
,
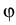
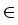
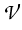 .
More general than in the above description of the model, we assume
that the interaction between particles can be described by means of a
(possibly nonlinear and nonlocal) Lipschitz continuous
interaction operator
.
More general than in the above description of the model, we assume
that the interaction between particles can be described by means of a
(possibly nonlinear and nonlocal) Lipschitz continuous
interaction operator
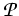 :
: 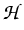
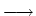
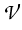 .
.
Applying fixed-point arguments and comparison principles
in [4], we show
that for every initial value g 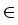 S there exists a solution
(u, w)
S there exists a solution
(u, w) 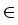
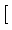
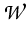
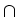
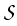
![$ \left.\vphantom{ \mathcal{W} \cap \mathcal{S} }\right]$](img187.gif) x
x 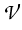 of the evolution system
of the evolution system
u' + 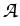 (u, w) = 0 , w = (u, w) = 0 , w = 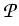 u , u(0) = g . u , u(0) = g .
|
(5) |
Moreover, under some natural regularity assumption on the
interaction operator
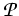 :
: 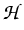
 in [4] we also get the unique solvability of our problem.
In fact, we additionally assume that
in [4] we also get the unique solvability of our problem.
In fact, we additionally assume that
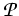 has the Volterra property
and that the restriction of
has the Volterra property
and that the restriction of
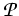 to
to
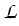
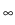 is a Lipschitz continuous operator from
is a Lipschitz continuous operator from
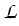
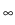 into a certain Sobolev-Morrey space
into a certain Sobolev-Morrey space
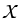
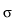
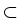
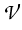 for some parameter
for some parameter
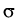 > m .
Then, our regularity theory for initial boundary value problems with
nonsmooth data in Sobolev-Morrey and Hölder spaces
(see [3]) enables us to prove
the unique solvability of problem (5).
> m .
Then, our regularity theory for initial boundary value problems with
nonsmooth data in Sobolev-Morrey and Hölder spaces
(see [3]) enables us to prove
the unique solvability of problem (5).
To illustrate our results, we consider an example of a ternary system,
where the interaction operator
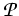 :
: 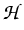
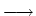
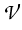 is defined by
(
is defined by
(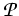 u)k = (Ku)k - (Ku)0 ,
k
u)k = (Ku)k - (Ku)0 ,
k 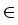 {1,..., n}
(see (3), (4), (5)).
The corresponding matrix kernel
{1,..., n}
(see (3), (4), (5)).
The corresponding matrix kernel 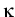 is chosen such that
particles of the same type attract and particles of different
type repel each other with the same range and strength of interaction.
Figures 1 and 2 show simulation results of phase separation processes
in a unit square.
Notice that both initial configurations contain equal numbers of black,
white, and red particles, respectively.
Moreover, the final states are local minimizers of the free energy functional
F under the constraint of particle number conservation.
is chosen such that
particles of the same type attract and particles of different
type repel each other with the same range and strength of interaction.
Figures 1 and 2 show simulation results of phase separation processes
in a unit square.
Notice that both initial configurations contain equal numbers of black,
white, and red particles, respectively.
Moreover, the final states are local minimizers of the free energy functional
F under the constraint of particle number conservation.
Fig. 1:
Phase separation process
for an initial value which is constant in the vertical direction.
The stripe pattern is preserved during the whole evolution.
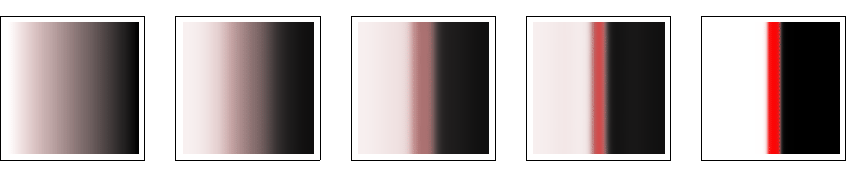 |
Fig. 2:
Phase separation process
for a symmetric initial value. There occur metastable states.
Finally, the phases are separated by a straight line and circular arcs.
 |
References:
- H. GAJEWSKI, K. ZACHARIAS,
On a nonlocal phase separation model,
J. Math. Anal. Appl., 286 (2003), pp. 11-31.
- G. GIACOMIN, J.L. LEBOWITZ, R. MARRA,
Macroscopic evolution of particle systems
with short- and long-range interactions,
Nonlinearity, 13 (2000), pp. 2143-2162.
- J.A. GRIEPENTROG,
Zur Regularität linearer elliptischer und parabolischer
Randwertprobleme mit nichtglatten Daten,
Logos-Verlag, Berlin, 2000, 219 pages.
- , On the unique solvability of
a phase separation problem for multicomponent systems,
WIAS Preprint no. 898, 2004,
to appear in: Banach Cent. Publ.
LaTeX typesetting by I. Bremer
2004-08-13
![]() {0, 1,..., n} occupying a spatial domain. In our model we assume
that the particles jump around on a given microscopically scaled lattice
following a stochastic exchange process (see [2]).
On each lattice site sits exactly one particle (exclusion principle).
Two particles of type k and l change their sites x and y
with probability
pkl(x, y) due to diffusion and
nonlocal interaction.
The hydrodynamical limit leads to a system of conservation laws
for
k
{0, 1,..., n} occupying a spatial domain. In our model we assume
that the particles jump around on a given microscopically scaled lattice
following a stochastic exchange process (see [2]).
On each lattice site sits exactly one particle (exclusion principle).
Two particles of type k and l change their sites x and y
with probability
pkl(x, y) due to diffusion and
nonlocal interaction.
The hydrodynamical limit leads to a system of conservation laws
for
k ![]() {0, 1,..., n},
{0, 1,..., n},