|
|
|
[Contents] | [Index] |
Kooperation: A. Ignat (Universität Iasi, Rumänien)
Beschreibung der Forschungsarbeit:
Die Untersuchungen befassten sich mit der Modellierung der
Deformation eines beidseitig eingespannten Bogens der Dicke
![]() , der durch eine Kurve
, der durch eine Kurve ![]() beschrieben wird. Sind
beschrieben wird. Sind ![]() die am Bogen angreifende Kraft und
die am Bogen angreifende Kraft und ![]() die Krümmung des Bogens, so führt (in lokalen
Koordinaten) das Kirchhoff-Love-Modell (Verwendung
des Dirichlet-Prinzips) auf die
Variationsaufgabe
die Krümmung des Bogens, so führt (in lokalen
Koordinaten) das Kirchhoff-Love-Modell (Verwendung
des Dirichlet-Prinzips) auf die
Variationsaufgabe
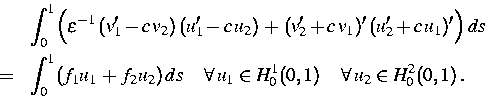
Die Unbekannten ![]() stellen dabei die tangentiale
bzw. normale Verschiebung des Bogens dar, d.h. es gilt
stellen dabei die tangentiale
bzw. normale Verschiebung des Bogens dar, d.h. es gilt
![]() , wobei
, wobei
![]() der Tangenteneinheitsvektor und
der Tangenteneinheitsvektor und ![]() der
Normaleneinheitsvektor sind.
der
Normaleneinheitsvektor sind.
Damit (1) sinnvoll ist, wurde bisher üblicherweise in der
Literatur (vgl. z.B. [1], [2]) angenommen, dass ![]() , d.h.
, d.h. ![]() , gilt. Unter dieser Annahme erhält man eindeutige
Lösbarkeit.
, gilt. Unter dieser Annahme erhält man eindeutige
Lösbarkeit.
Durch diese hohe Glattheitsforderung konnten bisher praktisch
wichtige Fälle, wie z.B. gothische Bögen, nicht behandelt
werden. Es ist ein Ziel der Untersuchungen, diese Einschränkung
zu überwinden. Hierzu wurde eine neue variationelle
Formulierung hergeleitet, die auf Methoden der optimalen
Steuerung beruht und auch für den Fall ![]() , d.h. für Bögen mit Ecken, anwendbar ist.
, d.h. für Bögen mit Ecken, anwendbar ist.
Es seien dazu ![]() und
und ![]() die eindeutige
Lösung der Zweipunktrandwertaufgabe
die eindeutige
Lösung der Zweipunktrandwertaufgabe
| (10) |
| (11) |
Finde ![]() mit (P)
mit (P)
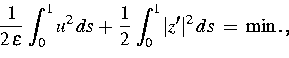
| (12) |
| (13) |
Ferner ergibt sich Folgendes: Schreibt man die notwendigen Optimalitätsbedingungen für (P) (oder für das duale Problem) in Form des Pontryagin'schen Maximum-Prinzips, so erhält man eine spezielle Dekomposition von (1) in ein System von Differentialgleichungen erster Ordnung mit Zweipunkt-Randbedingungen. In dieser Hinsicht stellt der neue Ansatz eine Fortsetzung der von Sprekels und Tiba (vgl. [3,4,5]) entwickelten Ideen für Platten und Stäbe dar.
Als weitere Aufgabenstellungen wurden Probleme der Shape
Optimierung für (1) untersucht. Hierbei sind ![]() (oder c) so zu bestimmen, dass für ein gegebenes Kräftepaar
(oder c) so zu bestimmen, dass für ein gegebenes Kräftepaar
![]() die resultierende Deformation bestimmte
gewünschte Eigenschaften besitzt. Ein typisches Beispiel ist es,
die Deformation
die resultierende Deformation bestimmte
gewünschte Eigenschaften besitzt. Ein typisches Beispiel ist es,
die Deformation ![]() in Normalenrichtung im Sinne der
in Normalenrichtung im Sinne der
![]() -Norm zu minimieren. Es ist im Berichtszeitraum
gelungen, die Existenz einer Lösung dieses nichtkonvexen
Optimierungsproblems für Lipschitz-stetige Bögen nachzuweisen
und die notwendigen Optimalitätsbedingungen erster Ordnung
herzuleiten.
-Norm zu minimieren. Es ist im Berichtszeitraum
gelungen, die Existenz einer Lösung dieses nichtkonvexen
Optimierungsproblems für Lipschitz-stetige Bögen nachzuweisen
und die notwendigen Optimalitätsbedingungen erster Ordnung
herzuleiten.
Die theoretischen Resultate und die Ergebnisse erster numerischer Tests sind in [6] dokumentiert.
Projektliteratur:
|
|
|
[Contents] | [Index] |