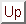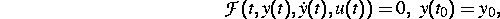

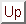


Beschreibung der Forschungsarbeit:
Forschungsgegenstand sind parallelisierbare numerische Verfahren zur Lösung von Anfangswertproblemen großer Systeme von Algebro-Differentialgleichungen (DAE)
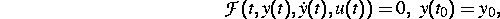
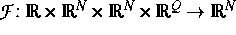 ,
,
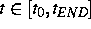 ,
, 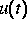 gegeben,
gegeben, 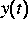 gesucht,
wie sie etwa bei der Prozeßsimulation chemischer Anlagen oder in der
Schaltkreissimulation auftreten.
gesucht,
wie sie etwa bei der Prozeßsimulation chemischer Anlagen oder in der
Schaltkreissimulation auftreten.
Solche Systeme sind oftmals schon durch die Modellierung entsprechend ihrer funktionellen Bestandteile in Teilsysteme strukturiert. Die von uns betrachteten Block-Waveform-Iterationsverfahren [1] weisen günstige Voraussetzungen für eine Parallelisierung auf der Ebene der DAE-Systeme auf. Sie sind jedoch nur für solche Aufgabenklassen anwendbar, für die eine für diese Verfahren geeignete Blockzerlegung bestimmt werden kann. Für DAE-Systeme, bei denen aufgrund starker Kopplungen zwischen den Teilsystemen keine solche Blockzerlegungen existieren, betrachten wir parallelisierbare strukturierte Newton-Verfahren. Hierbei werden die DAE-Systeme nach ihrer Zeitdiskretisierung in geeignet erweiterte nichtlineare Gleichungssysteme mit spezieller Blockstruktur überführt [2] und nach Linearisierung über die parallele Behandlung linearer Teilgleichungssysteme gelöst.
Bei einstufig strukturierten Verfahren werden die inneren Variablen
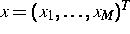 und die äußeren Variablen
und die äußeren Variablen 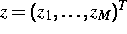 der Teilsysteme
der Teilsysteme 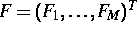 bestimmt und das um
Identifikationsgleichungen für äußere Variablen erweiterte System
bestimmt und das um
Identifikationsgleichungen für äußere Variablen erweiterte System
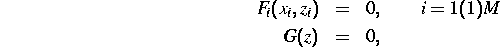
erzeugt. Wir partitionieren dann 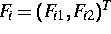 so, daß
so, daß
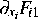 regulär ist. Dabei erfolgt die Auswahl der
Gleichungen
regulär ist. Dabei erfolgt die Auswahl der
Gleichungen 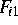 mit Hilfe eines Algorithmus zur
Pivotwahl in den überbestimmten Teilmatrizen
mit Hilfe eines Algorithmus zur
Pivotwahl in den überbestimmten Teilmatrizen 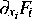 .
Die Bestimmung der Inkremente für einen Schritt des Newtonverfahrens
erfolgt in 3 Teilschritten:
.
Die Bestimmung der Inkremente für einen Schritt des Newtonverfahrens
erfolgt in 3 Teilschritten:
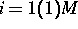 : Bestimme die Vektoren
: Bestimme die Vektoren
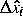 und
und 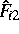 sowie die Matrizen
sowie die Matrizen
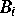 und
und 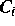 aus:
aus:
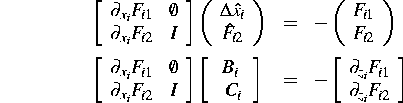
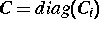 und
und 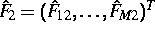 die äußeren Variablen
die äußeren Variablen 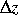 aus:
aus:

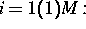 Berechne die inneren Variablen
Berechne die inneren Variablen
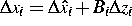 .
.
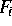 disjunkt sind,
können die Schritte (i) und (iii) für alle Blöcke
disjunkt sind,
können die Schritte (i) und (iii) für alle Blöcke
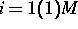 unabhängig voneinander und damit parallel ausgeführt
werden. Mehrstufig strukturierte Newton-Verfahren erhält man, wenn
man dieses Vorgehen rekursiv anwendet.
unabhängig voneinander und damit parallel ausgeführt
werden. Mehrstufig strukturierte Newton-Verfahren erhält man, wenn
man dieses Vorgehen rekursiv anwendet.Einstufig strukturierte Newtonverfahren wurden von uns implementiert und an praxisrelevanten Beispielen getestet. Sie haben sich dabei als moderat parallele Verfahren erwiesen.
Projektliteratur: