ClusCorr98 - Cluster Analysis and Data Analysis

ClusCorr98: Adaptive cluster analysis, classification and multivariate graphics

Methods of cluster analysis, classification and multivariate graphics can be used in order to extract hidden knowledge from huge data sets containing numerical and non-numerical information. Usually this task can be done in a better way by using statistical (mainly explorative) methods based on adaptive distance measures as proposed by Mucha (1992) in Clusteranalyse mit Mikrocomputern, Akademie Verlag, Berlin.

The Statistical Software

The spreadsheet environment of Microsoft Excel hosts the statistical software ClusCorr98. This software is in the Visual Basic for Applications language. Internal and external databases are easily accessed from the Excel environment, see H.-J. Mucha, H. H. Bock (1996): Classification and multivariate graphics: models, software and applications. WIAS Report No. 10, Berlin, and Mucha and Ritter (2009): Classification and clustering: Models, software and applications. WIAS Report No. 26, Berlin. Figure 1 shows a flowchart of an application of cluster analysis to archaeometry.

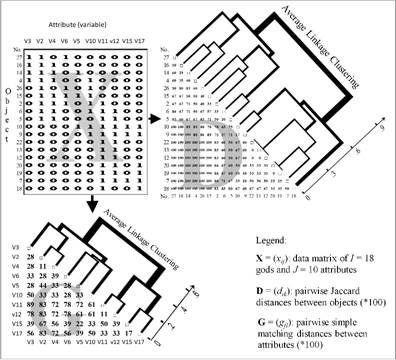
Fig. 1. From data to distances and then finally to results of (hierarchical) clustering.

Model-Based Gaussian Clustering

Model-based Gaussian clustering allows to identify clusters of quite different shapes, see the application to ecology in Figure 2.

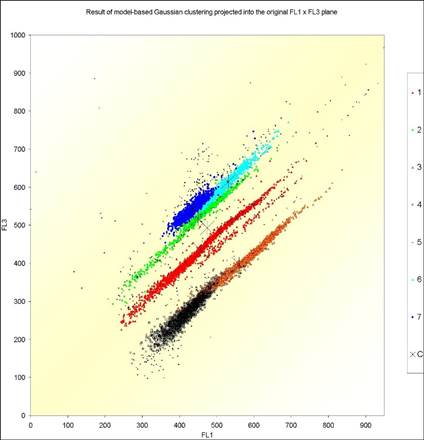
Fig. 2. Application of model-based Gaussian clustering to ecology. For details, see H.-J. Mucha, U. Simon, R. Brüggemann (2002): Model-based Cluster Analysis Applied to Flow Cytometry Data of Phytoplankton. Technical Report 5, WIAS, Berlin.

Parameterizations of the covariance matrix in the Gaussian model and their geometric interpretation are discussed in detail in Banfield and Raftery (1993): Model-Based Gaussian and Non-Gaussian Clustering, Biometrics, 49, 803–821. In the following, as a special approach in big data clustering, let us propose simple Gaussian core-based clustering. The simplest Gaussian model is when the covariance matrix of each cluster is constrained to be diagonal. Let X=(x_ij) be a data matrix with I row points (observations) and J column points (variables). Then the sum of squares criterion

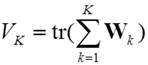(1)

has to be minimized, where

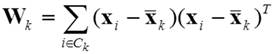(2)

is the sample cross-product matrix for the kth cluster. Criterion (1) can be expressed without using mean vectors of clusters k by

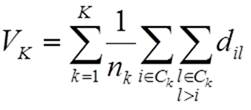, (3)

where d_ij are the usual pairwise squared Euclidean distances between observations. Here n_kdenotes the number of observations of the kth cluster.

In the more general case, when the covariance matrix of each cluster is constrained to be diagonal, but otherwise allowed to vary between the groups C_k, then the logarithmic sum-of-squares criterion

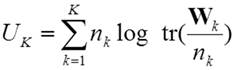(4)

has to be minimized. Again, an equivalent formulation based on pairwise distances holds for the logarithmic sum-of-squares criterion, namely:

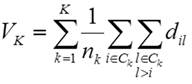. (5)

Core-based Clustering

(3) and (5) can be generalized by using non-negative weights of observations w_i instead of the neglected standard weights w_i = 1 that lead to n_k as the cardinality of cluster C_k. That’s one of the key ideas for working with cores instead of working with observations. For more details, see the already above given reference Mucha et al. (2002).

Clustering techniques based on cores (representative points) are appropriate tools for data mining of large data sets. Really, a huge amount of observations can be analysed in an efficient way. So, hierarchical clustering of millions of observations is possible. Moreover, the influence of outliers is reduced. Simulation studies were carried out in order to compare core-based clustering techniques with well-known model-based ones.

In case of big data, the methods based on clustering of cores (representative points, mean vectors) can be recommended. Cores represent regions of high density. More generally, a core represents a set of observations with small distances between one to each other.

Simulation Experiments

One example will be given here. There are 250 artificially generated Gaussian samples of size 250 with equal class probabilities drawn (K = 2 clusters). Each class is drawn from a multivariate normal distribution with unit covariance matrix. Class 1 has mean (a, a, …, a) and class 2 has mean (-a, -a, …, -a) with a = (4/J )^1/2. The samples are analysed in a parallel fashion by the following seven partitioning (p) and hierarchical (h) cluster analysis techniques K-Means (criterion (1), p), Ward ((3), h), WardV ((5), h), DistEx ((3), p), DistVEx ((5), p), DistExCore ((3), p), and DistVExCore ((5), p).

Partitioning methods start with an initial (random) partition and proceed by exchanging observations between clusters. All partitioning methods except K-Means are using pairwise distances between observations only. The last two methods work with 40 cores instead of 250 observations. The cores are figured out from each sample by using distance restrictions. Ward and WardV are hierarchical clustering methods that result in a set of nested partitions into K = 2, 3, 4, … clusters. Figure 3 shows that K-Means, DistExCore, and DistVExCore perform best. However the last two give the most stable results.

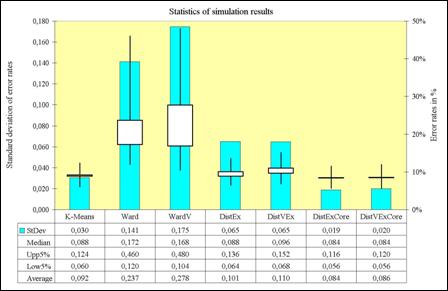
Fig 3. Summary of simulation results of clustering two normals N(a, 1) and N(-a, 1) with a = (4/J )^1/2, where J = 20 is the number of dimensions.

These results as well as other simulation experiments (especially those with samples containing outliers) verify that core-based clustering methods perform very well and become stable against outliers. Moreover, core-based clustering also induced give good results in practical applications.

Fig 4. Fingerprint of the distance matrix of Roman bricks (extract).

An Application

Cluster analysis attempts to divide a set of objects (observations) into smaller, homogeneous and at least practical useful subsets (clusters). Objects that are similar one to another form a cluster, whereas dissimilar ones belong to different clusters. Here similar means that the characteristics of any two objects of the same cluster should be close to each other in a well-founded sense. Once a distance measure between objects is derived (multivariate) graphical techniques can be used in order to give some insights into the data under investigation.

Figure 4 presents a graphical output of a distance matrix, a so-called heat map. Figure 5 shows the result of the core-based clustering of Roman bricks and tiles.

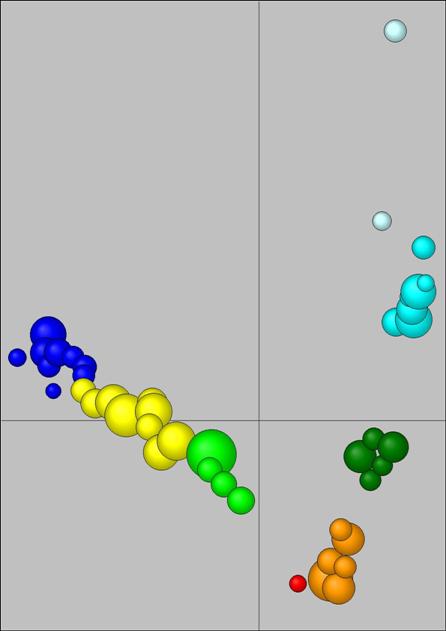
Fig 5. Principal component analysis plot of the result of core-based clustering of 613 observations (Roman bricks).

Variable Selection in Clustering

Nowadays, latest practical relevant improvements are based on a proposed bottom-up variable selection technique. Figure 6 shows the result of a successful application to archaeometry that is accepted for publication in the TOPOI (excellence cluster) series.

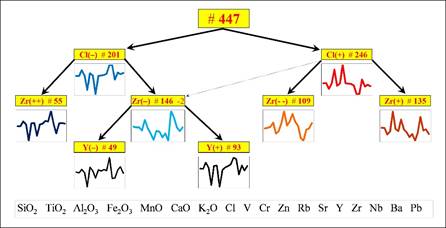
Fig. 6. Cluster tree obtained by a new bottom-up variable selection clustering procedure.

Built-in Validation by Resampling

The built-in validation is the heart of ClusCorr98. It is based on resampling techniques such as bootstrapping. It performs three level of validation. The most general one is: What is the number of clusters? Then in more detail, the investigation of stability of individual clusters is performed. Figure 7 shows a typical result of built-in validation of each individual cluster.

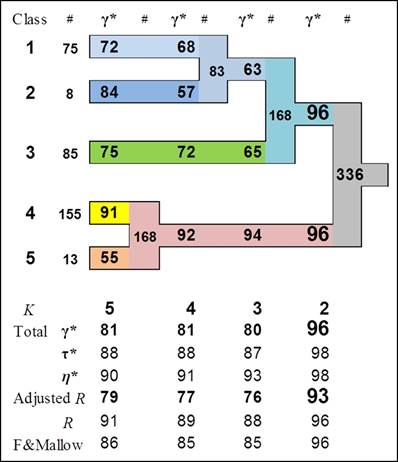
Fig. 7. Investigation of stability of clusters (data source: the Troia archaeological excavation project).

When (real) clusters were found, then the profile of clusters should reflect this, as shown in Figure 8. Validation in most possible detail is the third level: assessment of the reliability of each observation to its cluster.

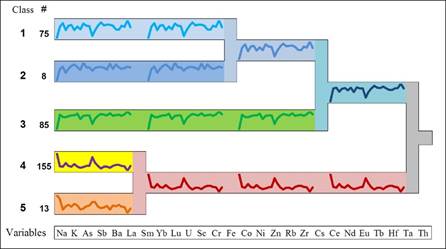
Fig. 8. Informative dendrogram after investigation of stability of clusters (data source: the Troia archaeological excavation project).