Collaborator: J. Geiser,
O. Klein,
P. Philip (until August 2004),
J. Sprekels
Cooperation with: Ch. Meyer, F. Tröltzsch
(Technische Universität Berlin),
K. Böttcher, D. Schulz, D. Siche
(Institut für Kristallzüchtung (IKZ),
Berlin),
P. Philip
(since September 2004 Institute for Mathematics and its Applications (IMA),
Minneapolis, USA)
Supported by: DFG Research Center MATHEON, project C9
Description:
![% latex2html id marker 42160
\minipage{0.55\textwidth}\Projektbild {\textwidth}...
...wth apparatus according to [\ref{lit7_sic_Pon}]
\label{fig7_sic_1}}
\endminipage](img614.gif) Owing to numerous technical applications in electronic and
optoelectronic devices,
the industrial demand for high quality silicon carbide (SiC)
bulk single
crystals remains large.
The most successful and most widely used growth technique of recent
years is the
sublimation growth of SiC bulk single crystals
via physical vapor transport (PVT),
also known as the
modified Lely method.
Owing to numerous technical applications in electronic and
optoelectronic devices,
the industrial demand for high quality silicon carbide (SiC)
bulk single
crystals remains large.
The most successful and most widely used growth technique of recent
years is the
sublimation growth of SiC bulk single crystals
via physical vapor transport (PVT),
also known as the
modified Lely method.
During PVT, a graphite crucible (see Figure 1) is
placed in a low-pressure inert gas atmosphere consisting of argon. The
crucible is then intensely heated, e.g., by induction
heating, to temperatures up to
3000 K. Inside the crucible, polycrystalline SiC source powder
sublimates, and the gaseous species diffuse through the cavity to the
SiC seed. As the single-crystalline seed is kept at a temperature
below that of the SiC source, the species crystallize on the seed,
which thereby grows into the reactor.
The physical and mathematical modeling of the growth process leads to a
highly nonlinear system of coupled partial differential equations.
In addition to the kinetics of a rare gas mixture at high temperatures,
one has to consider heat transport by conduction and radiation,
reactive matter transport through porous and granular media,
different kinds of chemical reactions and phase transitions, and
the electromagnetic fields and heat sources produced by the induction heater.
The main control parameters with respect to an optimization of the
crystal growth process are the design of the growth apparatus, the position
of the induction coil, the heating power, and the inert gas pressure.
Within the covered research period, the simulation software
WIAS-HiTNIHS
has been made more flexible, such that
the program can now deal with
more general geometries. During runtime, the program can read descriptions of
geometries from
ASCII files, in which the
geometry is described by a sequence of points followed by a list
of polygons.
Moreover, some preparations have been made to be able to use the output
of a program with a GUI allowing the input of geometry description
and the creation of meshes which is currently under development in
the Research Group
``Numerical Mathematics and Scientific Computing''.
To handle general geometries, the treatment of
radiation has been generalized, such that also radiation
regions with a boundary consisting of several connected
components can be considered, i.e. such that one can also deal with
radiation regions surrounding some opaque objects.
For two points (r, z) and (s, y) on the (r, z)
boundary of the radiation
region one has to determine the visibility intervals, i.e.
the intervals for 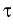 such that the points
(r,
such that the points
(r,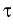 , z) and (s, 0, y) (expressed in cylindrical coordinates)
are mutually visible, since the ray connecting these points
is not blocked by any part of the crucible.
Following [1], this is done
by considering the circular projection of these rays.
In Figure 2, we present the circular projection
of rays connected to the boundaries of the visibility intervals.
, z) and (s, 0, y) (expressed in cylindrical coordinates)
are mutually visible, since the ray connecting these points
is not blocked by any part of the crucible.
Following [1], this is done
by considering the circular projection of these rays.
In Figure 2, we present the circular projection
of rays connected to the boundaries of the visibility intervals.
Fig. 2:
Circular projections of rays corresponding to
the angles being either the begin (blue lines) or the end (red lines)
of visibility intervals for a radiation region surrounding four
opaque objects
![\makeatletter
\@DreiProjektbilderNocap[h]{0.3\textwidth}{fb04_7_02_sic_fig2.eps}{fb04_7_02_sic_fig3.eps}{fb04_7_02_sic_fig4.eps}
\makeatother](img615.gif) |
The handling of material parameters has been made more flexible,
and WIAS-HiTNIHS now reads the material parameters
during runtime from a material data file, see [2].
Moreover, the programming of a software
with a GUI to create and edit such material data files has been
started.
We have also taken into account the direction dependence of the
thermal conductivity of
the insulation of the crucible.
Considering the coordinates (r, z),
a heat flux 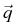 of the form
of the form
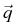 = -
= - 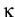 (T)
(T)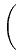
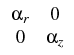
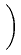 grad T is used,
where
T is the temperature,
grad T is used,
where
T is the temperature,
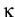 is a temperature-dependent thermal conductivity,
and
is a temperature-dependent thermal conductivity,
and
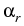 ,
, 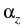 are given positive constants.
A FVM discretization for this term has been derived and
implemented in WIAS-HiTNIHS.
Some results can be found in Figure 3.
are given positive constants.
A FVM discretization for this term has been derived and
implemented in WIAS-HiTNIHS.
Some results can be found in Figure 3.
Some mathematical optimization problems connected to the SiC growth process
are considered in [3], [4].
There, semilinear elliptic equations with nonlocal interface
conditions are treated,
modeling the diffuse-gray
conductive-radiative heat transfer within the growth apparatus.
Based on a minimum principle for the semilinear equation, as well
as L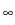 estimates for the weak solution,
the existence of an optimal solution and necessary
optimality conditions have been established. The theoretical results are illustrated by results
of numerical computations.
estimates for the weak solution,
the existence of an optimal solution and necessary
optimality conditions have been established. The theoretical results are illustrated by results
of numerical computations.
Fig. 3:
Computation for isotropic and anisotropic insulations. In the left figure,
we have an isotropic insulation with
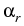 =
= 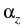 = 1,
in the middle figure, we have z-anisotropy
with
= 1,
in the middle figure, we have z-anisotropy
with
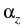 = 1000 for all insulation parts, and in the right figure for the
upper and lower parts of the insulation, we have r anisotropy with
= 1000 for all insulation parts, and in the right figure for the
upper and lower parts of the insulation, we have r anisotropy with
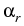 = 1000, and for the remaining parts of the insulation,
we have z anisotropy with
= 1000, and for the remaining parts of the insulation,
we have z anisotropy with
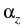 = 1000.
= 1000.
![\makeatletter
\@DreiProjektbilderNocap[h]{0.2\textwidth}{fb04_7_02_sic_fig5.eps}{fb04_7_02_sic_fig6.eps}{fb04_7_02_sic_fig7.eps}
\makeatother](img622.gif) |
References:
- F. DUPRET, P. NICODEME, Y. RYCKMANS, P. WOUTERS, M.J. CROCHET,
Global modelling of heat transfer in crystal growth furnaces,
Int. J. Heat Mass Transfer, 33(9) (1990), pp. 1849-1871.
- J. GEISER, O. KLEIN, P. PHILIP,
WIAS-HiTNIHS: A software tool for simulation in sublimation
growth of SiC single crystals: Applications and methods,
to appear in the Proceedings of the International Congress of
Nanotechnology and Nano World Expo 2004.
- C. MEYER, P. PHILIP, F. TRÖLTZSCH,
Optimal control of a semilinear PDE with nonlocal radiation
interface conditions,
WIAS Preprint no. 976, 2004
, submitted.
- C. MEYER, P. PHILIP,
Optimizing the temperature profile during sublimation growth of
SiC single crystals: Control of heating power, frequency, and coil
position, WIAS Preprint no. 895, 2003
,
Crystal Growth & Design, 5 (2005), pp. 1145-1156.
- M. PONS, M. ANIKIN, K. CHOUROU,
J.M. DEDULLE, R. MADAR, E. BLANQUET,
A. PISCH, C. BERNARD, P. GROSSE,
C. FAURE, G. BASSET, Y. GRANGE,
State of the art in the modelling of SiC sublimation growth,
Materials Science and Engineering B, 61-62 (1999),
pp. 18-28.
LaTeX typesetting by H. Pletat
2005-07-29
![% latex2html id marker 42160
\minipage{0.55\textwidth}\Projektbild {\textwidth}...
...wth apparatus according to [\ref{lit7_sic_Pon}]
\label{fig7_sic_1}}
\endminipage](img614.gif) Owing to numerous technical applications in electronic and
optoelectronic devices,
the industrial demand for high quality silicon carbide (SiC)
bulk single
crystals remains large.
The most successful and most widely used growth technique of recent
years is the
sublimation growth of SiC bulk single crystals
via physical vapor transport (PVT),
also known as the
modified Lely method.
Owing to numerous technical applications in electronic and
optoelectronic devices,
the industrial demand for high quality silicon carbide (SiC)
bulk single
crystals remains large.
The most successful and most widely used growth technique of recent
years is the
sublimation growth of SiC bulk single crystals
via physical vapor transport (PVT),
also known as the
modified Lely method.
![\makeatletter
\@DreiProjektbilderNocap[h]{0.3\textwidth}{fb04_7_02_sic_fig2.eps}{fb04_7_02_sic_fig3.eps}{fb04_7_02_sic_fig4.eps}
\makeatother](img615.gif)
![\makeatletter
\@DreiProjektbilderNocap[h]{0.2\textwidth}{fb04_7_02_sic_fig5.eps}{fb04_7_02_sic_fig6.eps}{fb04_7_02_sic_fig7.eps}
\makeatother](img622.gif)