[Next]:

Applied mathematical finance and stochastic simulation

[Up]:

Projects

[Previous]:

Projects

 [Contents] 

 [Index] 

Subsections

• 1. Adaptive smoothing procedures
• 2. Imaging
• 3. Classification and density estimation
• 4. Analysis of biosignals
• 5. Modeling of financial time series and volatility estimation
• 6. Inference for partly linear regression
• 7. Search of non-Gaussian components of a high-dimensional distribution
• 8. Inverse problems
• 9. Cluster analysis and data mining

Statistical data analysis

Collaborator: D. Belomestny, V. Essaoulova, A. Hutt, P. Mathé, D. Mercurio, H.-J. Mucha, J. Polzehl, M. Reiß, V. Spokoiny

Cooperation with: R. Brüggemann, Ch. Heyn, U. Simon (Institut für Gewässerökologie und Binnenfischerei, Berlin), P. Bühlmann (ETH Zürich, Switzerland), C. Butucea (Université Paris X, France), M.-Y. Cheng (National Taiwan University, Taipeh), A. Daffertshofer (Free University of Amsterdam, The Netherlands), A. Dalalyan (Université Paris VI, France), J. Dolata (Universität Frankfurt am Main), J. Fan (Princeton University, USA), J. Franke (Universität Kaiserslautern), R. Friedrich (Universität Münster), J. Gladilin (Deutsches Krebsforschungszentrum, Heidelberg), H. Goebl, E. Haimerl (Universität Salzburg, Austria), A. Goldenshluger (University of Haifa, Israel), I. Grama (Université de Bretagne-Sud, Vannes, France), J. Horowitz (Northwestern University, Chicago, USA), A. Juditski (Université de Grenoble, France), N. Katkovnik, U. Ruatsalainen (Technical University of Tampere, Finland), Ch. Kaufmann (Humboldt-Universität zu Berlin), K.-R. Müller (Fraunhofer FIRST, Berlin), A. Munk (Universität Göttingen), M. Munk (Max-Planck-Institut für Hirnforschung, Frankfurt am Main), S.V. Pereverzev (RICAM, Linz, Austria), P. Qiu (University of Minnesota, USA), H. Riedel (Universität Oldenburg), B. Röhl-Kuhn (Bundesanstalt für Materialforschung und -prüfung (BAM), Berlin), A. Samarov (Massachusetts Institute of Technology, Cambridge, USA), M. Schrauf (DaimlerChrysler, Stuttgart), S. Sperlich (University Carlos III, Madrid, Spain), U. Steinmetz (Max-Planck-Institut für Mathematik in den Naturwissenschaften, Leipzig), P. Thiesen (Universität der Bundeswehr, Hamburg), C. Vial (ENSAI, Rennes, France), Y. Xia (National University of Singapore), S. Zwanzig (Uppsala University, Sweden)

Supported by: DFG: Priority Program 1114 ``Mathematische Methoden der Zeitreihenanalyse und digitalen Bildverarbeitung''(Mathematical methods for time series analysis and digital image processing); DFG Research Center MATHEON, project A3

Description:

The project Statistical data analysis focuses on the development, theoretical investigation and application of modern nonparametric statistical methods, designed to model and analyze complex data structures. WIAS has, with main mathematical contributions, obtained authority for this field, including its applications to problems in technology, medicine, and environmental research as well as risk evaluation for financial products.

Methods developed in the institute within this project area can be grouped into the following main classes.

1. Adaptive smoothing procedures

(D. Belomestny, V. Essaoulova, J. Polzehl, V. Spokoiny).

Research on adaptive smoothing methods is driven by challenging problems from imaging and time series analysis. Applications to imaging include reconstruction of 2D and 3D images from Magnetic Resonance Tomography or microscopy, signal detection in functional Magnet Resonance Imaging (fMRI) experiments, or edge recovery from Positron Emission Tomography (PET) data.

The models and procedures proposed and investigated at WIAS are based on three main approaches: pointwise adaptation, originally proposed in [57] for estimation of regression functions with discontinuities and extended to images in [38], propagation-separation or adaptive weights smoothing, proposed in [39] in the context of image denoising, and stagewise aggregation, introduced in [3].

The main idea of the pointwise adaptive approach is to search, in each design point, for the largest acceptable window that does not contradict the assumed local model, and to use the data within this window to obtain local parameter estimates. This allows for estimates with nearly minimal variance under controlled bias.

Stagewise aggregation, see [3], is defined as a pointwise adaptation scheme based on an ordered sequence of ``weak'' local likelihood estimates $\tilde{{\theta}}^{{(k)}}_{}$(x) of the local parameter $\theta$(x) at a fixed-point x ordered due to decreased variability. Starting from the most variable and least biased estimate $\tilde{{\theta}}^{{(1)}}_{}$(x), the procedure sequentially defines the new estimate $\hat{{\theta}}^{{(k)}}_{}$ as a convex combination of the next ``weak'' estimate $\tilde{{\theta}}^{{(k)}}_{}$(x) and the previously computed estimate $\hat{{\theta}}^{{(k-1)}}_{}$(x) in the form

$$\hat{{\theta}}^{{(k)}}_{}$$(x) = $$\gamma_{{k}}^{}$$$$\tilde{{\theta}}^{{(k)}}_{}$$(x) + (1 - $$\gamma_{{k}}^{}$$)$$\hat{{\theta}}^{{(k-1)}}_{}$$(x),

where the coefficient $\gamma_{{k}}^{}$ may depend on the location x and is defined by comparing two estimates $\hat{{\theta}}^{{(k-1)}}_{}$(x) and $\tilde{{\theta}}^{{(k)}}_{}$(x). The proposed method yields a new aggregated estimate whose pointwise risk does not exceed the smallest risk among all ``weak'' estimates multiplied by some logarithmic factor. The paper [3] establishes a number of important theoretical results concerning optimality of the aggregated estimate and shows a good performance of the procedure in simulated and real-life examples.

The general concept behind the propagation-separation approach, see [43, 44], is structural adaptation. The procedure attempts to recover for each point the largest neighborhood where local homogeneity with respect to a prespecified model is not rejected. This is achieved in an iterative process by extending regions of local homogeneity (propagation) as long as this does not contradict the structural information obtained in previous iteration steps. Points are separated into different regions if their local parameter estimates become significantly different within the iteration process. This class of procedures is derived from adaptive weights smoothing, as introduced in [39, 41, 42], by adding stagewise aggregation as a control step. This allowed to put the procedures from [41, 42] into a unified and slightly simpler concept and to prove theoretical properties for the resulting estimates.

The propagation-separation approach possesses a number of remarkable properties like preservation of edges and contrasts and nearly optimal noise reduction inside large homogeneous regions. It is almost dimension free and applies in high-dimensional situations. Moreover, if the prespecified model is valid globally, both stagewise aggregation and the propagation-separation approach yield the global estimate. Both procedures are rate optimal in the pointwise and global sense.

2. Imaging

(A. Hutt, J. Polzehl, V. Spokoiny).

The propagation-separation approach enables us to handle locally smooth images [43], see Figure 1 for an example, and local constant likelihood estimation for exponential family models [44] in a unified way. The latter allows, e.g., for images containing Poisson counts, binary or halftone images, or images with intensity-dependent gray value distributions. We now expect to have the necessary understanding and tools to extend the approach to locally smooth exponential family models.

Fig. 1: Reconstruction of a piecewise smooth image by local quadratic propagation-separation and stagewise aggregation

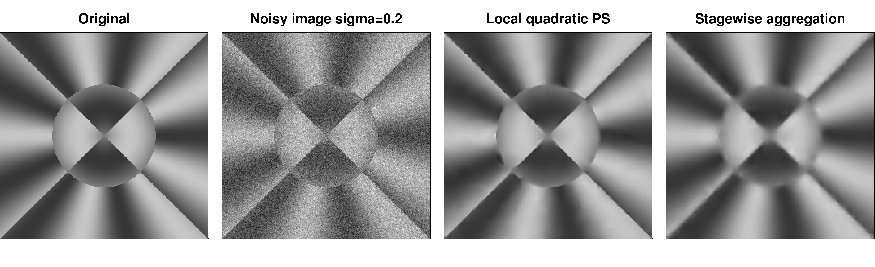Stagewise aggregation turns out to be more suitable for smooth images. It is less sensitive to edges, see again Figure 1, but on the other hand less dependent on the prespecified local model. Due to its less involved structure it allows for much faster implementations and therefore different classes of applications.

3. Classification and density estimation

(D. Belomestny, J. Polzehl, V. Spokoiny).

In [44], the propagation-separation approach is used to derive a class of classification procedures based on a binary response model. This allows to improve on classical nonparametric procedures like kernel regression and the nearest-neighbor by weakening the problem of optimal parameter choice.

The equivalence of Poisson regression and density estimation allows to extend both the propagation-separation approach and stagewise aggregation to the problem of density estimation. The applicability of the propagation-separation approach from [44] is, being based on a local constant structural assumption, currently restricted to densities with pronounced discontinuities. This limitation will be removed with the extension of the approach to generalized linear models.

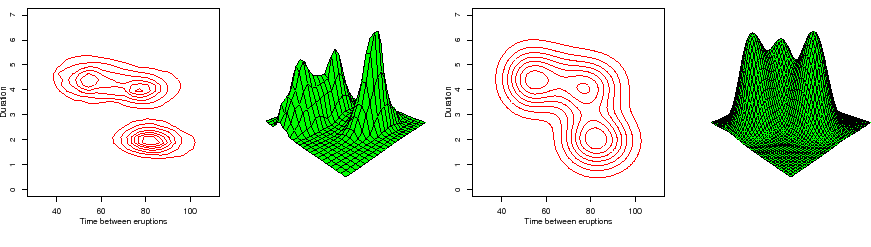
Stagewise aggregation allows for excellent estimates for smooth densities. Figure 2 illustrates the density estimates obtained for the Old Faithful Geyser data set.

Fig. 2: Contour and perspective plots of density estimates obtained by the stagewise aggregation procedure (top) and bivariate kernel smoothing (bottom) for the Old Faithful Geyser data set

4. Analysis of biosignals

(A. Hutt, J. Polzehl, V. Spokoiny).

A growing number of real-life problems in medicine and biosciences lead to the statistical analysis of large data sets with unknown complex structure. The well-developed statistical theory for traditional parametric models or for uni-(low-)dimensional functional data cannot directly be applied for many of these data sets. We aim to develop novel methods for biomedical signal processing based on neural networks and nonlinear nonstationary time series models. In addition, we tried to combine these methods with microscopic models of biomedical activity to further improve the developed methods. We attack the problem of analysis and modeling of biomedical signals. In one part, the synchronization of multivariate brain signals is investigated by a fixed-point clustering algorithm. It turns out that functional brain processes generate transient signal states, which exhibit global phase synchronization on a dramatically decreased time scale. In a second part, the project aims to model these signal states by neural activity models. Here, we study the spatiotemporal dynamics of neural population activity concerning its stability [1, 18, 19, 20, 22].

5. Modeling of financial time series and volatility estimation

(D. Mercurio, J. Polzehl, V. Spokoiny).

Our approach for time series focuses on local stationary time series models. These methods allow for abrupt changes of model parameters in time. Applications for financial time series include volatility modeling, volatility prediction, risk assessment.

ARCH and GARCH models gained a lot of attention and are widely used in financial engineering since they have been introduced in [4, 11]. The simple GARCH(1,1) model is particularly popular suggesting a very natural and tractable model with only three parameters to be estimated. Moreover, this model allows to mimic many important stylized facts of financial time series like volatility clustering (alternating periods of small and large volatility) and persistent autocorrelation (slow decay of the autocovariance function of the absolute or squared returns). The GARCH models are successfully applied to short term forecasting of the volatility and particularly to Value-at-Risk problems, see also the project Applied mathematical finance.

However, it appears that the most crucial problem in the GARCH approach is that GARCH models are not robust w.r.t. violation from the stationarity assumption. If the stationarity assumption is violated, GARCH modeling is essentially reduced to exponential smoothing of the last observed squared returns. [33, 34] also argued that the other stylized facts of financial time series like long-range dependence, persistent autocorrelation, and the integration GARCH effect can be well explained by nonstationarity in the observed data.

Our approach to model local stationary time series is based on the assumption of local homogeneity: For every time point there exists an interval of time homogeneity in which the volatility parameter can be well approximated by a constant. The pointwise adaptive procedure from [32] recovers this interval from the data using local change-point analysis. Then the estimate of the volatility can be simply obtained by local averaging. The performance of the procedure is investigated both theoretically and through Monte Carlo simulations. A comparison with the LAVE procedure from [31] and with a standard GARCH model is provided.

In [45], a general class of GARCH models with time-varying coefficients is introduced. The adaptive weights approach is extended to estimate the GARCH coefficients as a function of time. This is based on a localization of the GARCH model by local perturbation of the likelihood function that allows to test for equivalence of two local models. A simpler semiparametric model in which the nonlinear parameter is fixed is discussed. The performance of the parametric, time-varying non- and semiparametric GARCH(1,1) models and the local constant model from [41] is assessed by means of simulated and real data sets using different forecasting criteria. Our results indicate that the simple local constant model outperforms the other models in almost all cases. The GARCH(1,1) model demonstrates a relatively good forecasting performance as far as the short-term forecasting horizon is considered. However, its application to long-term forecasting seems questionable because of possible misspecification of the model parameters.

In [46], a non-parametric, non-stationary framework for business-cycle dating is developed based on the adaptive weights smoothing techniques from [41, 42]. The methodology is used both for the study of the individual macroeconomic time series relevant to the dating of the business cycle as well as for the estimation of their joint dynamics. Since the business cycle is defined as the common dynamics of some set of macroeconomic indicators, its estimation depends fundamentally on the group of series monitored. Our dating approach is applied to two sets of US economic indicators including the monthly series of industrial production, nonfarm payroll employment, real income, wholesale-retail trade, and gross domestic product (GDP). We find evidence of a change in the methodology of the NBER's Business-Cycle Dating Committee: In the dating of the largest recession, an extended set of five monthly macroeconomic indicators replaced the set of indicators emphasized by the NBER's Business-Cycle Dating Committee in recent decades. This change seems to seriously affect the continuity in the outcome of the dating of business cycles. Had the dating been done on the traditional set of indicators, the last recession would have lasted one year and a half longer. We find that, independent of the set of coincident indicators monitored, the last economic contraction began in November 2000, four months before the date of the NBER's Business-Cycle Dating Committee.

6. Inference for partly linear regression

(V. Spokoiny).

In [55], the authors proposed a new method of analysis of a partially linear model whose nonlinear component is completely unknown. The target of analysis is the indentification of the set of regressors which enter in a nonlinear way in the model function, and the complete estimation of the model including slope coefficients of the linear component and the link function of the nonlinear component. The procedure also allows for selecting the significant regression variables. We also develop a test of linear hypothesis against a partially linear alternative, or, more generally, a test that the nonlinear component is M-dimensional for M = 0, 1, 2,.... The method of analysis goes back to the idea of structural adaptation from [16, 17], where the problem of dimension reduction was considered for a single and multiple index model, respectively. The new approach is very general and fully adaptive to the model structure. The only restrictive assumption is that the dimensionality of the nonlinear component is relatively small. The theoretical results indicate that the procedure provides a prescribed level of the identification error and estimates the linear component with the accuracy of order n^-1/2. A numerical study demonstrates a very good performance of the method even for small or moderate sample sizes.

7. Search of non-Gaussian components of a high-dimensional distribution

(V. Spokoiny).

Suppose X₁,..., X_n is an i.i.d. sample in a high-dimensional space IR^d drawn from an unknown distribution with density f (x). A general multivariate distribution is typically too complex to be recovered from the data, thus dimension reduction methods need to be used to decrease the complexity of the model [2, 8, 54, 56, 60]. Many such dimension reduction techniques rely on some linear representation of data. For instance, PCA projects the data into the orthogonal principal component basis that are defined via the eigenvalue decomposition of the covariance matrix of the vector X. This method is well suited for the case of a normal distribution, because orthogonality implies independence of components for a multivariate Gaussian distribution. However, in practical situations, especially if the assumption of normality is violated, PCA can easily reach its limits.

An alternative approach, the Independent Component Analysis, assumes that the data is a linear transformation of a d-dimensional vector with independent components. Usually these components are assumed to be strictly non-Gaussian except for one Gaussian component to ensure their identifiability [6, 23]. Note that independent components do not necessarily form an orthogonal basis.

In [58], a new approach that allows to bridge these two completely different modeling approaches is developed. The model assumption is that the random vector X can be decomposed into a product of multivariate Gaussian and purely non-Gaussian components leading to the semiparametric class of densities

f (x) = g(Tx)$$\phi_{{\theta,\Gamma}}^{}$$(x)

where T is a linear mapping from IR^d to another space IR^m with m$\le$d, g is an unknown function in IR^m, and $\phi_{{\theta,\Gamma}}^{}$ is a normal density with the mean $\theta$ and the covariance matrix $\Gamma$. Note that this model includes as particular cases both the pure parametric (m = 0) and pure nonparametric (m = d) models. The first numerical results indicate a very reasonable performance of the method, while the theoretical results show that the procedure provides a prescribed level of the identification error.

8. Inverse problems

(P. Mathé, J. Polzehl, M. Reiß, V. Spokoiny).

Ill-posed equations arise frequently in the context of inverse problems, where it is the aim to determine some unknown characteristics of a physical system from data corrupted by measurement errors.

An estimation method based on pointwise recovering of the support function of a planar convex set from noisy observations of its moments is developed in [13]. Intrinsic accuracy limitations in the shape-from-moments estimation problem are shown by establishing a lower bound on the rate of convergence of the mean squared error. The proposed estimator is near-optimal in the sense of the order. [14] considers the problem of recovering edges of an image from noisy Positron Emission Tomography (PET) data. The original image is assumed to have a discontinuity jump (edge) along the boundary of a compact convex set. The Radon transform of the image is observed with noise, and the problem is to estimate the edge. We develop an estimation procedure which is based on recovering the support function of the edge. It is shown that the proposed estimator is nearly optimal in order in a minimax sense. Numerical examples illustrate reasonable practical behavior of the estimation procedure.

For ill-posed problems it is often impossible to get sensible results unless special methods, such as Tikhonov regularization, are used. Work in this direction is carried out in collaboration with S.V. Pereverzev, RICAM Linz. We study linear problems where an operator A acts injectively and compactly between Hilbert spaces, and the equation is disturbed by noise. Under a priori smoothness assumptions on the exact solution x, such problems can be regularized. Within the present paradigm, smoothness is given in terms of general source conditions, expressed through the operator A as x = $\varphi$(A*A)v,| v| $\leq$ R, for some increasing function $\varphi$, $\varphi$(0) = 0. This approach allows to treat regularly and severely ill-posed problems in a unified way. The study [25] provides a general approach to determine the degree of ill-posedness for statistical ill-posed problems and thus the intrinsic complexity for such problems. Moreover, in [28] the numerical analysis could be extended to statistical ill-posed problems, including the issue of discretization and adaptation, when the smoothness of the true solution is not known a priory.

Adaptive parameter choice strategies date back to the original paper by Phillips [30] and it became an important issue how this can be given a sound mathematical basis. Based on new tools for variable Hilbert scales, as developed in [27], the discrepancy principle is thoroughly analyzed in [26] while in [29], its extension to discretization was considered. The analysis results in a new algorithm, which allows to take into account the advantages of the discrepancy principle while classical projection methods do not.

Ergodic scalar diffusion processes of the type

$$\sigma \in$$ (1)

form an archetype model for time-dependent data. The nonparametric estimation problem for b based on continuous or high-frequency observations is well studied, cf. [24], and the asymptotic results for long-time asymptotics T$\to$$\infty$ resemble those for standard regression models. In [9], this relationship has been corroborated in the strong sense of Le Cam's equivalence for statistical experiments. This allows an immediate transfer of asymptotic statistical theory between these two models and yields a more profound understanding of the model itself.

It is shown that the above diffusion model is asymptotically equivalent to the Gaussian white noise model given by the observation of

$$\sqrt{{\mu_0(x)}} \in$$ (2)

where $\mu_{0}^{}$ is the invariant density of X under the central parameter of the localization. The technical conditions imposed to obtain this result are basically a uniform ergodicity property and a minimal regularity of order 1/2 for the function b. The method of proof relies on a coupling scheme on the diffusion space using the local time of the process to obtain the analogue of a deterministic design. Based on the principal local result, a global asymptotic equivalence result is obtained and extensions into several directions like constructive equivalence, time discretization, and more general diffusion coefficients are possible.

Nonparametric estimation for diffusion processes based on low-frequency data is an intricate problem and had first been considered in [12] for compact state spaces. In [52], this approach has been generalized to diffusion processes with natural boundary conditions on the state space IR. This extension poses many new difficulties: On the probabilistic side, the corresponding infinitesimal generator is usually not compact anymore and its eigenfunctions are unbounded, while statistically the highly degenerate observation design causes a heteroskedastic noise structure.

Using warped wavelet bases and imposing conditions on the underlying Dirichlet form, some of the difficulties can be overcome and mathematical efficiency results are obtained. The procedure is based on projection estimators for the invariant density and the Markov transition operator and on spectral decomposition results. Numerical simulation results, implementing the method with an adaptive wavelet thresholding approach, support the feasibility of this estimation procedure.

Inverse problems appear naturally in all areas of quantitative science, cf. the calibration problem described in the applied finance section. A statistical formulation is needed when modeling the error stochastically or when solving statistical inference problems for stochastic processes. An instance of the latter is the estimation of the delay length r in the affine stochastic differential equation

dX(t) = $$\Big($$$$\int_{{-r}}^{0}$$X(t + u)g(u) du$$\Big)$$ dt + $$\sigma$$ dW(t), t $$\in$$ [0, T].

In [52], an estimator for r from the observation (X(t), t $\in$ [0, T]) in the stationary case has been proposed. Assuming g(- r) $\not=$ 0, the estimation procedure is based on a change-point detection algorithm for a closely related inverse problem involving the empirical covariance operator, see also [50]. It consists of a two-step procedure using a cumulative sum (CUSUM) change-point detection for suitable wavelet coefficients. The rate of convergence for T$\to$$\infty$ corresponds to change point detection for a statistical inverse problem with degree one of ill-posedness.

The problem of an error in the operator, e.g., due to uncertainty about certain parameter values or due to numerical approximation errors, has been considered more fundamentally in [15]. The problem of recovering f $\in$ L² from the observation

$$\begin{cases}g_\epsilon=Kf+\epsilon\dot W\ K_\delta=K+\delta\dot B \end{cases}$$

is studied, where $\dot{{W}}$ denotes an L²-Gaussian white noise and $\dot{{B}}$ is a canonical operator Gaussian white noise. Assuming ellipticity and a degree t of ill-posedness, a nonlinear adaptive wavelet approach is developed, which generalizes the linear approach by [10] and the wavelet-Galerkin method of [5]. Minimax rates are obtained for the joint asymptotics $\delta$, $\epsilon$$\to$ 0. For functions f in d-dimensional Besov spaces B^s_{p, p}, the optimal rate of the integrated mean square error is max{$\delta$,$\epsilon$}^{${\frac{{4s}}{{2s+2t+d}}}$}, provided 1/p$\le$1/2 + s/(2t + d ) under certain minimal regularity conditions. Interestingly, the error in the operator does not yield a significant deterioration of the estimator as long as its level is below the error level in the data.

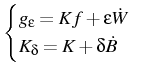
SIMEX was introduced in [7, 59] as a simulation-type estimator in errors-in-variables models. The idea of the SIMEX procedure is to compensate for the effect of the measurement errors while still using naive regression estimators. In [47, 48], a symmetrized version of this estimator is defined. Now [49] establishes some results relating these two simulation-extrapolation-type estimators to well-known consistent estimators like the total least squares estimator (TLS) and the moment estimator (MME) in the context of errors-in-variables models. We further introduce an adaptive SIMEX (ASIMEX). The main result of this paper is that SYMEX, ASIMEX are equivalent to total least squares. Additionally, we see that SIMEX is equivalent to the moment estimator.

9. Cluster analysis and data mining

(H.-J. Mucha).

Easy-to-understand graphical output of cluster analysis would be appreciated in the reality of a high-dimensional setting. To supply this need, new graphical outputs of hierarchical clustering are under development. Hierarchical cluster analysis is a well-known method of stepwise data compression. As a result one gets a dendrogram, that is, a special binary tree with a distinguished root and with all the data points (observations) at its leaves. Unfortunately, both the real or potential order of the objects and the potential quantitative locations of the objects are not reflected in the dendrogram. Often, neighboring objects in the dendrogram are quite distinct from one another in the reality of a heterogeneous, high-dimensional setting. Therefore, the reading of conventional dendrograms as well as their interpretation becomes difficult and it is often confusing. In [35], some dendrogram drawing and reordering techniques are recommended that reflect the total order in the one-dimensional case (univariate case) and, in the multivariate case, an order that corresponds approximately to a total order in some degree. The result, a so-called ordered dendrogram, is recommended because it makes the interpretation of hierarchical structures much easier.

Fig. 3: From global to local adaptive clustering: A graphical exemplification

Another focus is on the development of stable clustering techniques. Usually, a (global) cluster analysis model is applied first in order to find homogeneous subsets in data. As a result, ten or more clusters are detected in a heterogeneous data set. Often subsequent (or iterative) local cluster analyses perform better. This can be confirmed by using validation techniques [36]. By doing so, both the appropriate number of clusters can be validated and the stability of each cluster can be assessed. Figure 3 shows a successful application in archeometry. At the left-hand side, the overall cluster analysis result is presented based on the first two principal components. The clusters correspond to the high-density areas of the nonparametric bivariate density estimation. Several cuts of the density at different levels are shown. At the left-hand side of the figure, the local adaptive cluster analysis result corresponds to the two well-separated peaks of the bivariate density surface.

References:

1. F. ATAY, A. HUTT, Stability and bifurcations in neural fields with axonal delay and general connectivity, to appear in: SIAM J. Appl. Math.

2. M. BELKIN, P. NIYOGI, Laplacian eigenmaps for dimensionality reduction and data representation, Neural Computation, 15 (2003), pp. 1373-1396.

3. D. BELOMESTNY, V. SPOKOINY, Local likelihood modeling via stagewise aggregation, WIAS Preprint no. 1000, 2004.

4. T. BOLLERSLEV, Generalized autoregressive conditional heteroscedasticity, J. Econometrics, 31 (1986), pp. 307-327.

5. A. COHEN, M. HOFFMANN, M. REISS, Adaptive wavelet Galerkin methods for linear inverse problems, to appear in: SIAM J. Numer. Anal.

6. P. COMON, Independent component analysis - A new concept ?, Signal Processing, 36 (1994), pp. 287-314.

7. J.R. COOK, L.A. STEFANSKI, Simulation-extrapolation estimation in parametric measurement error models, J. Amer. Statist. Assoc., 89 (1994), pp. 1314-1328.

8. T.F. COX, M.A.A. COX, Multidimensional Scaling, Chapman & Hall, London, 2001.

9. A. DALALYAN, M. REISS, Asymptotic statistical equivalence for scalar ergodic diffusion processes, WIAS Preprint no. 916, 2004, to appear in: Probab. Theory Related Fields.

10. S. EFROMOVICH, V. KOLTCHINSKII, On inverse problems with unknown operators, IEEE Trans. Inform. Theory, 47 (2001), pp. 2876-2894.

11. R.F. ENGLE, Autoregressive conditional heteroscedasticity with estimates of the variance of UK inflation, Econometrica, 50 (1982), pp. 987-1008.

12. E. GOBET, M. HOFFMANN, M. REISS, Nonparametric estimation of scalar diffusions based on low frequency data, Ann. Statist., 32 (2004), pp. 2223-2253.

13. A. GOLDENSHLUGER, V. SPOKOINY, On the shape-from-moments problem and recovering edges from noisy Radon data, Probab. Theory Related Fields, 128 (2004), pp. 123-140.

14.          , Recovering edges of an image from noisy tomographic data, WIAS Preprint no. 909, 2004.

15. M. HOFFMANN, M. REISS, Nonlinear estimation for linear inverse problems with error in the operator, WIAS Preprint no. 990, 2004.

16. M. HRISTACHE, A. JUDITSKY, J. POLZEHL, V. SPOKOINY, Structure adaptive approach for dimension reduction, Ann. Statist., 29 (2001), pp. 1537-1566.

17. M. HRISTACHE, A. JUDITSKY, V. SPOKOINY, Direct estimation of the index coefficient in a single-index model, Ann. Statist., 29 (2001), pp. 595-623.

18. A. HUTT, Effects of nonlocal feedback on traveling fronts in neural fields subject to transmission delay, WIAS Preprint no. 953, 2004, Phys. Rev. E, 70 (2004), 052902, 4 pages.

19. A. HUTT, F. ATAY, Analysis of nonlocal neural fields for both general and gamma-distributed connectivities, WIAS Preprint no. 969, 2004.

20. A. HUTT, A. DAFFERTSHOFER, U. STEINMETZ, Detection of mutual phase synchronization in multivariate signals and application to phase ensembles and chaotic data, Phys. Rev. E, 68 (2003), 036219, 10 pages.

21. A. HUTT, T.D. FRANK, Stability, critical fluctuations and 1/f^$\alpha$-activity of neural fields involving transmission delays, Preprint no. 140 of DFG Research Center MATHEON, Technische Universität Berlin, 2004.

22. A. HUTT, M. SCHRAUF, Detection of transient generalized and mutual phase synchronization by clustering and application to single brain signals, WIAS Preprint no. 925, 2004.

23. A. HYVARINEN, J. KARHUNEN, E. OJA, Independent Component Analysis, Wiley, New York, 2001.

24. Y. KUTOYANTS, Statistical Inference for Ergodic Diffusion Processes, Springer, London [u.a.], 2004.

25. P. MATHÉ, Degree of ill-posedness of statistical inverse problems, WIAS Preprint no. 954, 2004.

26.          , What do we learn from the discrepancy principle?, manuscript written at RICAM, 2004.

27. P. MATHÉ, S.V. PEREVERZEV, Discretization strategy for linear ill-posed problems in variable Hilbert scales, Inverse Problems, 19 (2003), pp. 1263-1277.

28.          , Regularization of some linear ill-posed problems with discretized random noisy data, 2004, submitted.

29.          , The discretized discrepancy principle under general source conditions, manuscript, 2005.

30. D.L. PHILLIPS, A technique for the numerical solution of certain integral equations of the first kind, J. Assoc. Comput. Mach., 9 (1962), pp. 84-97.

31. D. MERCURIO, V. SPOKOINY, Statistical inference for time-inhomogeneous volatility models, Ann. Statist., 32 (2004), pp. 577-602.

32.          , Estimation of time dependent volatility via local change point analysis, WIAS Preprint no. 904, 2004.

33. T. MIKOSCH, C. STARICA, Is it really long memory we see in financial returns?, in: Extremes and Integrated Risk Management, P. Embrechts, ed., Risk Books, 2000.

34.          , Non-stationarities in financial time series, the long range dependence and the IGARCH effects, Rev. Econom. Statist., 86 (2004), pp. 378-390.

35. H.-J. MUCHA, H.-G. BARTEL, J. DOLATA, Techniques of rearrangements in binary trees (dendrograms) and applications, to appear in: Match.

36. H.-J. MUCHA, E. HAIMERL, Automatic validation of hierarchical cluster analysis with application in dialectometry, to appear in: Proceedings of the 28th Annual Conference of GfKl, Springer, Berlin.

37. H.-J. MUCHA, H.-G. BARTEL, J. DOLATA, Model-based cluster analysis of Roman bricks and tiles from Worms and Rheinzabern, to appear in: Proceedings of the 28th Annual Conference of GfKl, Springer, Berlin.

38. J. POLZEHL, V. SPOKOINY, Image denoising: Pointwise adaptive approach, Ann. Statist., 31 (2003), pp. 30-57.

39.          , Adaptive weights smoothing with applications to image restoration, J. Roy. Statist. Soc. Ser. B, 62 (2000), pp. 335-354.

40.          , Functional and dynamic magnetic resonance imaging using vector adaptive weights smoothing, J. Roy. Statist. Soc. Ser. C, 50 (2001), pp. 485-501.

41.          , Local likelihood modeling by adaptive weights smoothing, WIAS Preprint no. 787, 2002.

42.          , Varying coefficient regression modeling by adaptive weights smoothing, WIAS Preprint no. 818, 2003.

43.          , Spatially adaptive regression estimation: Propagation-separation approach, WIAS Preprint no. 998, 2004.

44.          , Propagation-separation approach for local likelihood estimation, manuscript, 2004.

45.          , Varying coefficient GARCH versus local constant volatility modeling. Comparison of the predictive power, WIAS Preprint no. 977, 2004.

46. J. POLZEHL, V. SPOKOINY, C. STARICA, When did the 2001 recession really start?, WIAS Preprint no. 934, 2004.

47. J. POLZEHL, S. ZWANZIG, On a symmetrized extrapolation estimator in linear errors-in-variables models, Comput. Statist. Data Anal., 47 (2004), pp. 675-688.

48.          , On a comparison of different simulation extrapolation estimators in linear errors-in-variables models, U.U.D.M. Report no. 17, 2003, Uppsala University.

49.          , SIMEX and TLS: An equivalence result, WIAS Preprint no. 999, 2004.

50. M. REISS, Adaptive estimation for affine stochastic delay differential equations, to appear in: Bernoulli.

51.          , Estimation of the delay length in affine stochastic delay differential equations, Internat. J. Wavelets Multiresolut. Inf. Process., 2 (2004), pp. 525-544.

52.          , Nonparametric volatility estimation on the real line from low-frequency observations, WIAS Preprint no. 911, 2004.

53. B. RÖHL-KUHN, J. POLZEHL, P. KLOBES, Simultaneous confidence and prediction bands in the certification of pressure-volume curves for the pore analysis of solids, manuscript, 2004.

54. S. ROWEIS, L. SAUL, Nonlinear dimensionality reduction by locally linear embedding, Science, 290 (2000), pp. 2323-2326.

55. A. SAMAROV, V. SPOKOINY, C. VIAL, Component identification and estimation in nonlinear high-dimensional regression models by structural adaptation, WIAS Preprint no. 828, 2003.

56. B. SCHÖLKOPF, A.J. SMOLA, K.-R. MÜLLER, Nonlinear component analysis as a kernel eigenvalue problem, Neural Computation, 10 (1998), pp. 1299-1319.

57. V. SPOKOINY, Estimation of a function with discontinuities via local polynomial fit with an adaptive window choice, Ann. Statist., 26 (1998), pp. 1356-1378.

58. V. SPOKOINY, G. BLANCHARD, M. SUGIYAMA, M. KAWANABE, K.-R. MÜLLER, In search of non-Gaussian components of a high-dimensional distribution, manuscript, 2004.

59. L.A. STEFANSKI, J.R. COOK, Simulation-extrapolation: The measurement error jackknife, J. Amer. Statist. Assoc., 90 (1995), pp. 1247-1256.

60. J.B. TENENBAUM, V. DE SILVA, J.C. LANGFORD, A global geometric framework for nonlinear dimensionality reduction, Science, 290 (2000), pp. 2319-2323.

[Next]:

Applied mathematical finance and stochastic simulation

[Up]:

Projects

[Previous]:

Projects

 [Contents] 

 [Index]