Microscopic modeling of financial assets

[Next]:

Stochastic models for biological populations

[Up]:

Projects

[Previous]:

Disordered systems and combinatorial optimization problems

[Contents]

[Index]

Microscopic modeling of financial assets

Collaborator: A. Bovier, J. Cerný

Cooperation with: O. Hryniv (University of Durham, UK)

Supported by: DFG Research Center MATHEON, project E1

Description:

The goal of this project is to develop and investigate more realistic models of order book dynamics that take into account the actual trading mechanisms involved in the price evolution. In this way, one hopes to bring methods and ideas from the theory of interacting random systems to bear on the fundamental theory of price processes in finance. Our modeling ansatz is to consider a Markovian time evaluation on the ``virtual order book'', i.e. the space of opinions on the value of an asset of all traders on the market (a trader, by definition, has the opinion that the value of an asset is p if he is willing to buy resp. sell the asset at the price p). An opinion is of the ask type if the trader wants to sell at this price, and of the bid type if he wants to buy at this price. An opinion state is stable iff no trades can be performed, i.e. if the lowest ask price exceeds the highest bid price. The current price is then the midpoint between these two values. In our model, traders change their opinion according to some random mechanism, and transactions are performed instantly to always keep the opinion state stable.

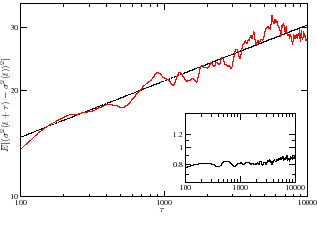
While the price formation mechanism in this model is realistic, the difficulty is to find suitable rules for the opinion changes of the traders. Simulations show that realistic price processes can only be achieved if the updating rules take a time-dependent environment (optimism/pessimism) into account. A reasonable scenario is a process of events (news/information) that trigger periods of optimism/pessimism of random strength and duration. Without much effort, this produces processes whose correlation structure has properties similar to real data.

**Fig. 1:** Volatility clustering in model with external influence. In the inset the same quantity for the original model.
$\ProjektEPSbildNocap{7cm}{bla.eps}$

Mathematically, one would like to obtain limit theorems that allow to characterize the properties of the price process resulting from such a model. This can at first only be done in rather simple versions of the model. A popular one is the B + S $\rightarrow$ $\emptyset$ model, introduced earlier by Bak et al. [3].

Here, the traders take opinions that belong to the set B_L = { - L, - L + 1,..., L}. The opinion of any trader performs a time-continuous simple random walk (possibly with a drift) in this set. If the opinion leaves B_L, then it disappears from the game. On the other hand, the buyers and sellers are injected at L, resp. - L with rates $\rho_{+}^{}$ and $\rho_{-}^{}$ . If a buyer meets a seller, they interchange the stock, and they both change their opinion in such a way that they leave B_L and are no longer considered.

In this context we could prove convergence of the empirical order book, in the limit when the number of traders goes to zero, under proper rescaling, to the solution of a nonlinear diffusion equation,

$\displaystyle {\frac{{\partial}}{{\partial t}}}$ $\displaystyle \rho$ (t, x)	=	$\displaystyle {\frac{{\partial^2}}{{\partial x^2}}}$ $\displaystyle \rho$ (t, x) + $\displaystyle \delta$ sign( $\displaystyle \rho$ (t, x)) $\displaystyle {\frac{\partial}{{\partial x}}}$ $\displaystyle \rho$ (t, x) x $\displaystyle \in$ (- 1, 1), t > 0,
$\displaystyle \rho$ (0, x)	=	$\displaystyle \rho_{0}^{}$ (x) x $\displaystyle \in$ [- 1, 1],
$\displaystyle \rho$ (t, - 1)	=	- c_- t > 0,
$\displaystyle \rho$ (t, + 1)	=	c₊ t > 0.

The proofs use techniques from the theory of hydrodynamic limits and large deviations [2].

References:

A. BOVIER, J. CERNÝ, O. HRYNIV, The opinion game: Stock price evolution from microscopic market modelling, WIAS Preprint no. 903, 2004, submitted.
, A + B $\rightarrow$ $\emptyset$ interface problems arising from a model of trading agents, in preparation.
P. BAK, M. PACZUSKI, M. SHUBIK, Price variations in a stock market with many agents, Physica A: Statistical and Theoretical Physics, 246 (1997), pp. 430-453.