Optimal control of production processes

[Next]:

Research Group Interacting Random Systems

[Up]:

Projects

[Previous]:

Optimization and inverse problems in diffractive

[Contents]

[Index]

Optimal control of production processes

Collaborator: I. Bremer, R. Henrion, D. Hömberg, M.H. Farshbaf Shaker, W. Weiss

Cooperation with: C. Chelminski (Cardinal St. Wyszynski University, Poland), D. Dentcheva (Stephens Institute of Technology, New Jersey, USA), H. Hämmerle (Rücker GmbH, Weingarten), A. Jourani (Université de Bourgogne, Dijon, France), A. Khludnev (Lavrentyev Institute of Hydrodynamics, Novosibirsk, Russia), U. Lindemann (Volkswagen AG, Wolfsburg), J. Outrata (Institute of Information Theory and Automation (UTIA) Prague, Czech Republic), W. Römisch (Humboldt-Universität zu Berlin), A. Seeger (Université d'Avignon, France), J. Soko $\l$ owski (IECN/INRIA Lorraine, Vandoeuvre-lès-Nancy, France), T. Szántai (Technical University of Budapest, Hungary), F. Tröltzsch (Technische Universität Berlin), S. Volkwein (Karl-Franzens-Universität Graz, Austria), M. Yamamoto (University of Tokyo, Japan)

Supported by: DFG-Forschungszentrum MATHEON, projects C7 & C11; Rücker GmbH; Volkswagen AG

Description:

1. Mean risk models for electricity portfolio management (R. Henrion).

Continuing the work initiated in this project, the focus was on scenario reduction in stochastic optimization. The multistage decision/observation structure of optimization problems with random data (like electricity demands or prices in power generating systems) is usually reflected in a scenario tree. Figure 1 (upper part) shows an example of a 4-stage tree with 7 branches at each node where branching probabilities are visualized by different gray values.

**Fig. 1:** Reduction of a scenario tree based on discrepancy distances
$\ProjektEPSbildNocap{0.5\textwidth}{fig4_rh.ps}$

The optimization problem induced by such trees may become too large to be solved efficiently. Hence, a careful reduction of such trees is a crucial prerequisite for their solution. The modification of a scenario tree can be interpreted as a perturbation of the underlying probability measure. A theoretically sound approach of carrying out such reduction relies on the use of suitable probability metrics which are well adapted to the problem class, [11]. Efficient scenario reduction algorithms have been obtained before in the case of purely continuous decision variables, [3]. A new challenge arises in case of additional discrete decision variables (e.g., on/off decisions for power generating units). The class of probability metrics to be considered then, in order to ensure that the reduced tree stays close to the original one, is given by discrepancy distances based on rectangles or cells. A solution method based on linear programming and capable of dealing with all discrepancy-type distances has been developed and implemented. Figure 1 (lower part) shows a reduced set of 10 out of originally 343 scenarios (again with gray values corresponding to probabilities) which minimizes the (cell-) discrepancy distance to the original tree.

Further works related to this project were concerned with solution stability in stochastic optimization ([4]), error bounds in nonlinear optimization ([5, 1]), and structural properties of quasi-concave probability measures ([6]).

2. Optimal control of surface heat treatments (D. Hömberg, W. Weiss).

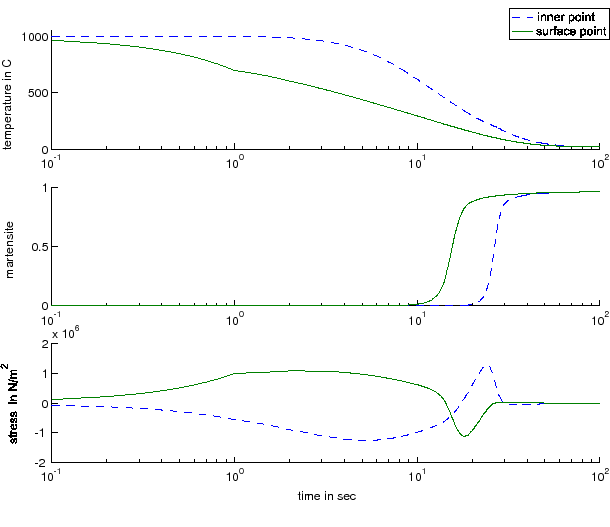
In [12], a simplified version of a thermomechanical model of phase transitions in steel ([7]) has been considered. Disregarding the transformation plasticity, numerical simulations with density depending on temperature and phase volume fractions show that the model is capable of reproducing the typical thermomechanical behavior of materials exhibiting phase transitions. Figure 2 shows the results of a numerical simulation where the lateral boundary of a steel cylinder has been cooled so fast that only martensite is produced. On top, one can see the evolution of temperature in the core and at the boundary of the cylinder. In the middle, the growth of the martensitic phase is depicted. The picture at the bottom shows the evolution of thermal stresses. Especially two stress reversals can be seen, which is a typical feature of materials exhibiting phase transitions during cooling.

**Fig. 2:** Evolution of temperature (top), phase volume fractions (middle), and thermal stress (bottom) for core and boundary of a cylinder cooled at the lateral boundary
$\ProjektEPSbildNocap{0.7\textwidth}{fig4_meline2en3.eps}$

Disregarding furthermore the temperature dependency of the density of the different phases and assuming instead that the main effect stems from the different thermal expansions of the respective phases, control problems for the resulting thermomechanical problem have also been investigated in [12].

Another natural approach is to generalize the usual equations of linearized thermoelasticity for the case of materials with phase transition by incorporating phase-dependent thermal expansion coefficients via a mixture ansatz. While in [8] a contact problem for such a model has been investigated, the aim of [2] is to investigate the related control problem.

**Fig. 3:** Snapshot of a simulation of laser surface hardening: adaptively refined grid (top), temperature and isolines of austenite volume fraction (bottom)
$\makeatletter \@ZweiProjektbilderNocap[v]{0.7\textwidth}{fig4_grid.eps}{fig4_laser.eps} \makeatother$

Concerning laser surface treatments, we have started to exploit the adaptivity features of pdelib2 in collaboration with Research Group 3 (see page ). As a first result, Figure 3 shows a snapshot of a laser hardening simulation. On top, the adaptively refined grid which moves with the laser focus is depicted. At the bottom, one can see the temperature and isolines of the austenite volume fraction. To resolve the thin austenitic layer, a second grid had to be introduced.

As has been described in last year's report, an efficient PID algorithm has been developed for controlling laser material treatments. As a partial justification for this approach we could prove the exact controllability of a linear parabolic equation along a curve. The result can also be extended to a semilinear heat equation (cf. [10]).

3. Path planning for industrial robots and human models in automotive industry (I. Bremer, R. Henrion, W. Weiss).

According to the demands of our cooperation partner, our work last year was centered around three tasks: time-optimal path-planning avoiding collisions, path-planning and simulation of cooperative robots, and a comparison between virtual reality and real world, to assure that robotic movements in a virtual shop-floor environment take the same time as in reality.

An additional challenge in this project is to maintain the real-time capabilities of complete shop-floor simulations including more than 100 active robots and further components.

**Fig. 4:** Avoidance of collisions with $\epsilon$ tolerance by including additional auxiliary points
in the robot path
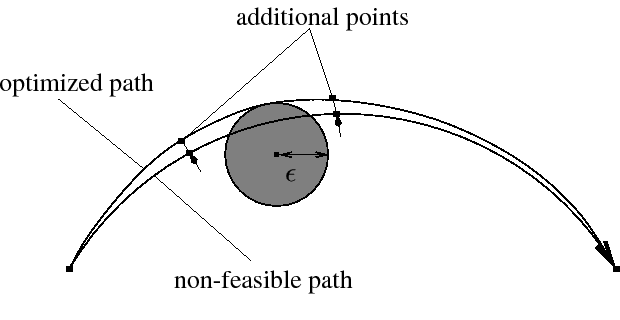$\ProjektEPSbildNocap{0.7\textwidth}{fig4_coll.ps}$

To avoid collisions between a robot and its surrounding, one has to compute a time-optimal path respecting a prescribed minimal distance to all objects in the scene. The circumvention of barriers is realized by introducing additional points in the robot path. If one uses the real geometry of theses barriers, the problem is high-dimensional and time-consuming. Instead, the geometries of the barriers are approximated by simple geometries, e.g., balls. Then the problem is reduced to computing the coordinates of additional auxiliary points in the robot path to obtain a time-optimal path which respects the minimal distance to a given point (cf. Figure 4).

A typical situation in which the employment of cooperative robots is beneficial is the case of one robot moving a workpiece with a gripper while another one performs some spot-welding tasks on that workpiece (cf. Figure 5). Compared to the usual inverse kinematics problem for one robot, the number of degrees of freedom is increased by 1 to 6, depending on prescriptions for the path of the partner robot. To compute a common pair of positions, an SQP method is used to minimize the position error subject to angle constraints in the robotic joints.

**Fig. 5:** Spot-welding of a car component using two cooperative robots
$\ProjektEPSbildNocap{0.7\textwidth}{fig4_kir.ps}$

4. Modeling and parameter identification for cost parameters of car factories (D. Hömberg, W. Weiss).

The aim of the project is the development of cost models in cooperation with our partner Volkswagen AG. The investments for the building of a car factory depend on a number of different variables, for example, the size of the cars, the produced number of cars per day, and the size of that part of the car which is really assembled in the respective factory. The typical number of variables is small, e.g., five. If the investment is known as a function of these variables, it is possible to optimize the costs for building a factory.

**Fig. 6:** Screenshot of `WIAS-ParKoM`. Here ``X...'' represent different confidential variables.
$\ProjektEPSbildNocap{0.7\textwidth}{fig4_screenshotx.eps}$

Unfortunately, there exist only few data sets of really existing factories in order to determine a decent cost model. Therefore, the desired formula should contain only a small number of free parameters, which may be determined by using the data of the really existing factories. Thus the most important part of the project was to find appropriate cost models based on plausible assumptions which are able to reproduce the given data with only few parameters and on the other hand allow for an extrapolation outside the given range of parameter values.

To solve the nonlinear regression problem, the software WIAS-ParKoM has been developed (cf. Figure 6). The free parameters in the model are determined by a hybrid optimization strategy. First a random search is used to find different possible local solutions, and then a conjugate gradient method is used to single out the best global solution. The software WIAS-ParKoM allows for calculating and plotting costs for arbitrary values of the variables together with the corresponding confidence intervals.

References:

P. BOSCH, A. JOURANI, R. HENRION, Sufficient conditions for error bounds and applications, Appl. Math. Optim., 50 (2004), pp. 161-181.
C. CHELMINSKI, D. HÖMBERG, Optimal control of a thermomechanical phase transition model, in preparation.
J. DUPACOVA, N. GRÖWE-KUSKA, W. RÖMISCH, Scenario reduction in stochastic programming: An approach using probability metrics, Math. Program., 95 (2003), pp. 493-511.
R. HENRION, W. RÖMISCH, Hölder and Lipschitz stability of solution sets in programs with probabilistic constraints, Math. Program., 100 (2004), pp. 589-611.
R. HENRION, J. OUTRATA, Calmness of constraint systems with applications, WIAS Preprint no. 929, 2004, to appear in: Math. Program.
R. HENRION, W. RÖMISCH, Lipschitz and differentiability properties of quasi-concave and singular normal distribution functions, 2005, submitted.
D. HÖMBERG, A mathematical model for induction hardening including mechanical effects, Nonlinear Anal. Real World Appl., 5 (2004), pp. 55-90.
D. HÖMBERG, A. KHLUDNEV, A thermoelastic contact problem with a phase transition, WIAS Preprint no. 914, 2004.
D. HÖMBERG, S. VOLKWEIN, W. WEISS, Optimal control strategies for the surface hardening of steel, in: Proceedings of the 2nd International Conference on Thermal Process Modelling and Computer Simulation, Nancy, France, March 31 - April 2, 2003, S. Denis, P. Archambault, J.-M. Bergheau, R. Fortunier, eds., vol. 120 of J. Physique IV, EDP Sciences, 2004, pp. 324-335.
D. HÖMBERG, M. YAMAMOTO, Exact controllability on a curve for a parabolic equation, in preparation.
W. RÖMISCH, Stability of stochastic programming problems, in: Stochastic Programming, A. Ruszczynski, A. Shapiro, eds., Handbooks Oper. Res. Management Sci., 10, Elsevier, Amsterdam, 2003, pp. 483-554.
M. SEIBOLD, Optimale Steuerung thermomechanischer Phasenübergänge in Stahl, diploma thesis, Technische Universität Berlin/Universität Karlsruhe, 2004.