Wave properties of four models describing

Cooperation with: C. Lai (European Centre for Training and Research in Earthquake Engineering, Pavia, Italy), R. Lancellotta (Politecnico di Torino, Italy)

Description: In this project (see: [1]) we investigate the propagation of bulk waves within the frame of four different linear two-component models of poroelastic materials. In the last year it has been shown by Wilmanski [3] that Biot's model may follow from a general nonlinear thermodynamical model solely in the case when such a nonlinear model contains a constitutive dependence on the porosity gradient and, if needed, on some other higher gradients. A full linear model following from such a generalization is as follows.

$\displaystyle {\frac{{\partial \rho ^{S}}}{{\partial t}}}$	=	- $\displaystyle \rho_{{0}}^{{S}}$ div v^S, $\displaystyle {\frac{{\partial \rho ^{F}}}{{\partial t}}}$ = - $\displaystyle \rho_{{0}}^{{F}}$ div v^F,
$\displaystyle \rho_{{0}}^{{S}}$ $\displaystyle {\frac{{\partial \mathbf{v}^{S}}}{{\partial t}}}$	=	div T^S + $\displaystyle \hat{{p}}$ + $\displaystyle \rho_{{0}}^{{S}}$ b^S,
$\displaystyle \rho_{{0}}^{{F}}$ $\displaystyle {\frac{{\partial \mathbf{v}^{F}}}{{\partial t}}}$	=	div T^F - $\displaystyle \hat{{p}}$ + $\displaystyle \rho_{{0}}^{{F}}$ b^F,

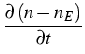$\displaystyle {\frac{{\partial \left( n-n_{E}\right) }}{{\partial t}}}$ = - $\displaystyle \Phi$ div $\displaystyle \left(\vphantom{ \mathbf{v}^{F}-\mathbf{v}^{S}}\right.$ v^F - v^S $\displaystyle \left.\vphantom{ \mathbf{v}^{F}-\mathbf{v}^{S}}\right)$ + $\displaystyle \hat{{n}}$ .

These balance equations transform into field equations if we add constitutive relations. For poroelastic materials they are assumed to have the form

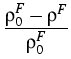T^S = T₀^S + $\displaystyle \lambda^{{S}}_{}$ e1 +2 $\displaystyle \mu^{{S}}_{}$ e^S + Q $\displaystyle \varepsilon$ 1, e : = tr e^S, $\displaystyle \varepsilon$ : = $\displaystyle {\frac{{\rho _{0}^{F}-\rho ^{F}}}{{\rho _{0}^{F}}}}$ ,

T^F = T₀^F + $\displaystyle \rho_{{0}}^{{F}}$ $\displaystyle \kappa$ $\displaystyle \varepsilon$ 1 + Qe1, n_E = n₀ $\displaystyle \left(\vphantom{ 1+\delta e}\right.$ 1 + $\displaystyle \delta$ e $\displaystyle \left.\vphantom{ 1+\delta e}\right)$ ,

$\displaystyle \hat{{p}}$ = $\displaystyle \pi$ $\displaystyle \left(\vphantom{ \mathbf{v}^{F}-\mathbf{v}^{S}}\right.$ v^F - v^S $\displaystyle \left.\vphantom{ \mathbf{v}^{F}-\mathbf{v}^{S}}\right)$ - N grad n.

Certainly, the effective (macroscopic) parameters $\lambda^{{S}}_{}$ , $\mu^{{S}}_{}$ correspond to classical Lamé constants, $\kappa$ describes the macroscopic compressibility of the fluid, $\delta$ is a parameter coupling equilibrium changes of porosity with volume changes of the skeleton e, and Q is the coupling parameter introduced by Biot. The permeability coefficient $\pi$ is related to the permeability appearing in the Darcy model of seepage. If the contribution of the porosity gradient which is characterized by the material parameter N is zero, the model is identical with the one proposed by Biot provided that we neglect in Biot's model added mass effects (relative accelerations). It has been shown that, for a class of granular materials for which one can apply Gassmann relations between macroscopic and microscopic (true) material parameters, Biot's model as a particular case with N = 0 is thermodynamically admissible. Consequently we may describe a porous material either by a model with N $\neq$ 0 and corresponding generalizations of Gassmann relations or by a model with N = 0 (Biot) with classical Gassmann relations.

We have also two other possibilities in which Biot's coupling between partial stresses described by the material parameter Q does not appear. Such a model has been introduced some ten years ago (see, e.g., [4], where both the model and some results for waves are presented) and its structure is similar to the so-called simple mixtures of fluids [2]. This model follows from Biot's model in which we substitute Q = 0 or from the full model with Q = 0 , N = 0. The results are not the same because the simplified model does not admit simple tests yielding Gassmann relations. Consequently, we may use either classical Gassmann relations if we consider the simplified model to be a particular case of Biot's model or generalized Gassmann relations if we consider the simplified model to be a particular case of the full model.

Wave analysis within the simplified model is much simpler than within Biot's model or the full model. This concerns particularly surface waves. It is desirable to know whether such an analysis may describe--at least qualitatively--wave properties which would follow from more general models.

We compare numerical results for the above-mentioned four possibilities. It is demonstrated that both speeds of propagation of P1, S, and P2 waves and their attenuations differ qualitatively but not quantitatively for different models. For porosities appearing in applications to soils ( n₀ $\sim$ 0.15 ÷ 0.4), these numerical differences are smaller than 10 % (see figure below). Due to a rather poor accuracy of dynamical measurements in real soils, this discrepancy seems to be acceptable.

Wave properties of four models describing poroelastic media