Melt-flow simulation in Czochralski growth

Cooperation with: K. Böttcher, W. Miller, U. Rehse (Institut für Kristallzüchtung (IKZ) Berlin)

Description: As a result of recent semiconductor technology, there is currently much interest in the growth of high-quality indium phosphide (InP) crystals. This is especially true in the fields of optoelectronics and radio frequency electronics. There it is known, for example, that InP-based electronic components can perform much more efficiently than the hitherto favored gallium arsenide (GaAs) or silicon, mainly because InP can operate at higher frequencies.

Since May 2003 we have been engaged in a collaborative project with the Institute for Crystal Growth (IKZ) in Berlin, which has involved comparison of 2D and 3D numerical transient-flow simulations performed with different solvers at each institute, as a precursor to experimental growth using the vapor-pressure-controlled Czochralski (VCz) equipment at IKZ (http://www.ikz-berlin.de/groups/ag.czhl/pview.php?lang=EN&opt=0&no=07). This method of growth is a variant on the liquid-encapsulated Czochralski (LEC) growth method; an important additional feature of the VCz method is that the crystal, melt, and encapsulant are placed in an insulated inner chamber, which can significantly reduce potentially damaging thermal stresses within the grown crystal. We have previously applied the method to modeling the growth of GaAs crystals, as documented in last year's report [1]. Subsequent results can be found in [2], [3]. A similar model to the one described therein can be applied to InP growth, i.e. the liquid mechanics are again described by a coupled thermo-hydrodynamic system comprising the incompressible Navier-Stokes equations and the heat-transport equation. A fundamental difference applies to the boundary conditions for temperature, specifically on the encapsulant/melt interface $\Gamma_{E}^{}$ and the crucible wall $\Gamma_{C}^{}$ . For the InP study, we have applied a Dirichlet condition on both boundary sections, based on advection-free global simulation data supplied by IKZ. This contrasts with the more simplified conditions of adiabaticity on $\Gamma_{E}^{}$ and Dirichlet value dependence derived from simple functions on $\Gamma_{C}^{}$ , as assumed for the GaAs study.

R_C	76.7 mm	$\nu$	1.62 `x` 10^-7 m²/s
$\rho$	5.05 `x` 10³ kg/m³	$\delta$ T	1 K
$\Omega_{C}^{}$	up to 30 rpm	$\Omega_{X}^{}$	up to 15 rpm
Pr	0.015	Ro	1

In our mathematical model, the flow variables are non-dimensionalized in a standard fashion, mainly using the crucible radius R_C (as characteristic length), the melt kinematic viscosity $\nu$ , the melt density $\rho$ , the temperature difference $\delta$ T between the crystal/melt interface $\Gamma_{X}^{}$ and the rim of the crucible, and the angular velocities of the crystal and crucible ( $\Omega_{X}^{}$ and $\Omega_{C}^{}$ , in turn). Industry-relevant values of these quantities are shown in Table 1 above, as well as the Prandtl number Pr and thermal Rossby (or Richardson) number Ro. Finally, a non-dimensional crystal radius r_X = 0.5 and a non-dimensional height h_T = 0.6 were chosen. As with the GaAs project, we have performed computations using both cylindrical and realistic geometry. Also our initial efforts have been directed towards the case of iso-rotation, with $\Omega_{C}^{}$ = $\Omega_{X}^{}$ , and this holds for the examples shown below. The Reynolds number is appropriately defined as: Re = $\Omega_{C}^{}$ R_C²/ $\nu$ .

First, in the case of cylindrical geometry, we have performed axisymmetric, and more recently, three-dimensional (3D) melt-flow simulations for Reynolds numbers ranging from 1000 to 8000, all with Ro = 1 , Pr = 0.015. Although these values are typically well below those required by industry (whose values lie inside the turbulent regime), the rich structure in the resultant flow behavior seems worthy of analysis in its own right. Moreover, it provides a good basis for comparing results obtained with our finite element solver NAVIER, and those provided by STHAMAS3D, a finite-volume code with upwinding implemented at IKZ. The latter is more dissipative than ours and may be better suited to computing flow properties more relevant to industry, especially time-averaged quantities such as crystal/melt interface shape, and mean frequencies. On the other hand, NAVIER seems to be better suited to capturing transient effects accurately. As in the case for the GaAs research, the steady axisymmetric state was found to be most unstable to 3D oscillatory instabilities; for iso-rotation with $\Omega_{X}^{}$ = $\Omega_{C}^{}$ for example, we have found that, while the 2D solver first exhibits transient behavior for Re $\approx$ 4500 (corresponding to 1.18 rpm), in the 3D simulation this value is just below 3000 (around 0.79 rpm).

**Fig. 1:** Time-history behavior of various quantities in a cylindrical crucible with Re = 3000, Ro = 1; top (from left to right): mean difference of successive solutions, Nusselt number at crystal/melt interface, temperature at an axial location; bottom (left to right): Radial, axial, and azimuthal velocity components at various non-axial locations. Here h_T = 0.6.
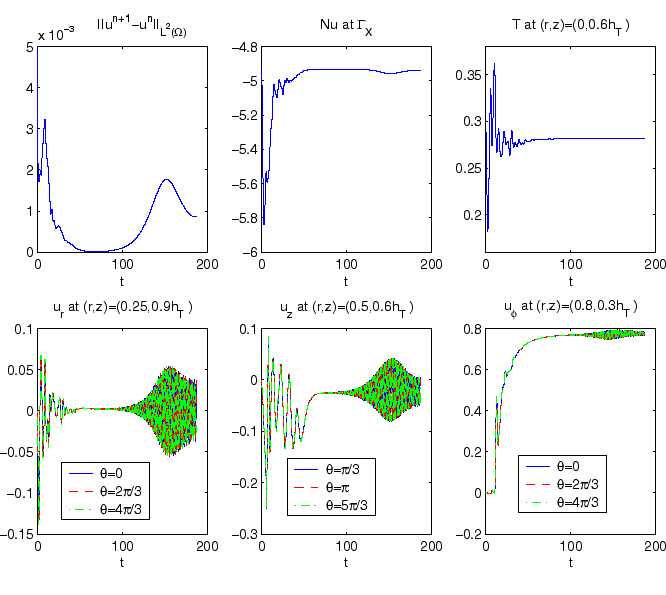$\ProjektEPSbildNocap{0.75\textwidth}{fig1_vcz.eps}$

In fig1_vcz.eps, we can see the time history plots for a selection of point data, as well as the Nusselt number on the crystal/melt interface and the mean difference between successive solutions; the relatively long ``swing-in'' phase which precedes oscillatory motion may suggest nearness to the critical Reynolds number. It is also noticeable from these plots that the high frequencies at this stage are purely associated with the three-dimensionality, with two-dimensional frequencies being very short, in comparison.

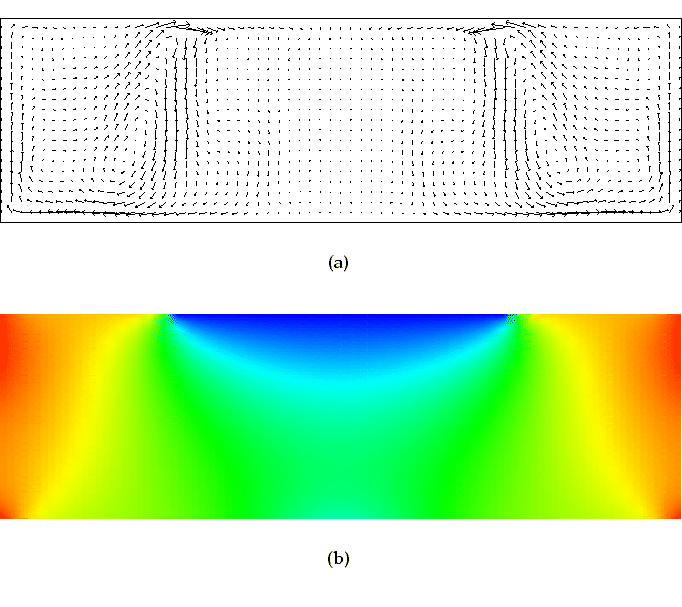
fig2_vcz.eps depicts the time-averaged flow and temperature profiles in an (almost) arbitrary vertical plane passing through the crucible and containing the axis. Here the time averaging was based on using a non-dimensionalized end time of 200 (or equivalently, running for 31.8 revolutions in dimensional terms). In fact, this solution is very similar to the axisymmetric component of the flow and reinforces the point regarding the relatively weak three-dimensional presence. Examination of the Fourier angle modes for various flow quantities reveals that the mode with azimuthal wavenumber 4 is the dominant 3D mode, although this is virtually indiscernible from cross-sectional slices of the crucible, so dominant is the axisymmetry. Another conclusion is that the flow is dominantly rotational with buoyancy playing a minor rôle here; the strongest non-rotational influence appears to stem from the large temperature gradient near the crystal/melt/encapsulant triple line (annulus).

**Fig. 2:** Time-averaged behavior in a typical vertical slice through the crucible showing (a) projected velocity (b) temperature for the test case Re = 3000, Ro = 1
$\ProjektEPSbildNocap{0.8\textwidth}{fig2_vcz.eps}$

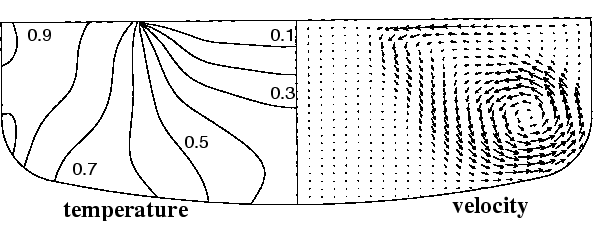
We have also recently applied our axisymmetric solver to simulating melt flows in crucibles of a more realistic design. The geometry here principally consists of a cylindrical flat-topped rim section joined to a spherical section, which itself is joined to a spherical cap of relatively large radius. Although similar qualitative features are found in comparison with using cylindrical geometry, early indications suggest that the former type is more de-stabilizing. In fig3_vcz.eps, for example, the solution is presented for Pr = 0.015 , Ro = 1, and Re = 3500 (0.92 rpm, approx.) portraying the time-averaged temperature and projected-velocity fields, based on a dimensionless end time of 100 (15.9 revolutions).

**Fig. 3:** Time-averaged solution for melt flow in a curve-based crucible for Re = 3500 , Ro = 1 , showing temperature contours to the left of the axis; projected velocity vectors to the right of the axis
$\ProjektEPSbildNocap{1.0\textwidth}{fig3_vcz.eps}$

In conclusion then, we have computed axisymmetric and 3D steady/transient melt-flow solutions for crucibles with cylindrical geometry, and axisymmetric steady/transient solutions using realistic geometry. In general, all of the results tend to suggest that, for Reynolds numbers up to 8000 at least, the flow is dominantly rotational, with the strongest non-rotational influence stemming from the triple line. For future work, we are principally interested in simulating transient 3D solutions using realistic geometry (in parallel with IKZ). Before this however, a realistic design of the meniscus at the triple line will be added, and suitable 3D meshes constructed.

Two- and three-dimensional unsteady melt-flow simulation in Czochralski InP crystal growth